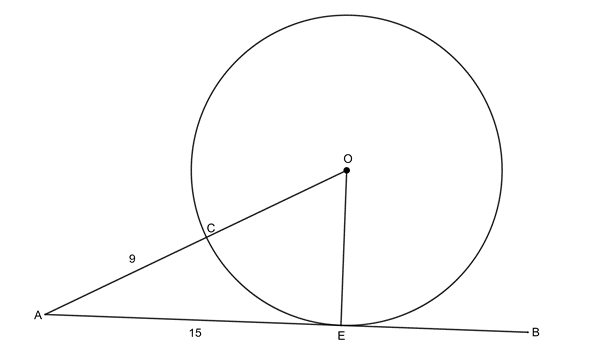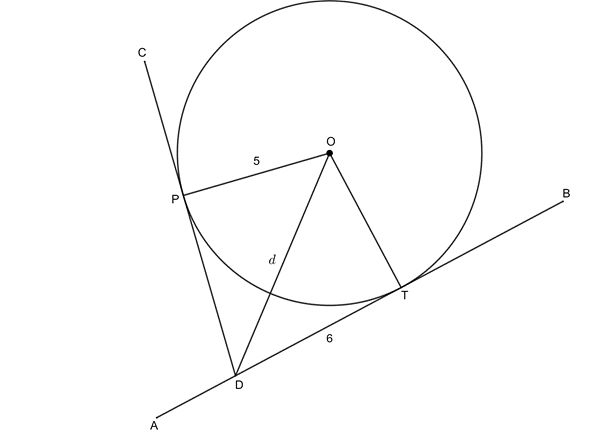Space, shape and measurement: Explore, interpret and justify geometric relationships
Unit 4: Tangent to circle theorems
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Apply the theorem tangent perpendicular to radius at point of contact.
- Apply the converse theorem of tangent perpendicular to radius.
- Apply the theorem two tangents drawn from the same point outside a circle are equal.
- Apply the tangent-chord theorem.
What you should know
Before you start this unit, make sure you can:
- State and use all the circle theorems covered in unit 2:
- A line drawn perpendicular to a chord from the centre of the circle bisects the chord.
- A line drawn from the circle centre to the mid-point of a chord is perpendicular to the chord.
- The angle subtended by an arc or chord at the centre of a circle is twice the size of the angle subtended at the circumference.
- The diameter of a circle subtends a right angle at the circumference.
- If an angle subtended by a chord at a point on the circumference is a right angle, then the chord is a diameter.
- Angles subtended by the same arc or chord in the same segment of a circle (on the same side of the chord) are equal.
- State and use all the cyclic quadrilateral theorems covered in unit 3:
- The opposite angles of a cyclic quadrilateral are supplementary.
- The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
- Prove that a quadrilateral is a cyclic quadrilateral. Refer to unit 3 if you need help with this.
Introduction
We have come across the concept of a tangent several times so far, most recently in subject outcome 3.1. We therefore know that a tangent is a straight line that touches a curve at one point and one point only.
In subject outcome 3.1, we dealt with finding the equation of a tangent to a circle. We noted that the tangent is perpendicular to the line drawn from the centre of the circle to the circumference at the point of tangency. We will use this fact as the basis for one of the theorems in this unit.
Tangent to circle theorems
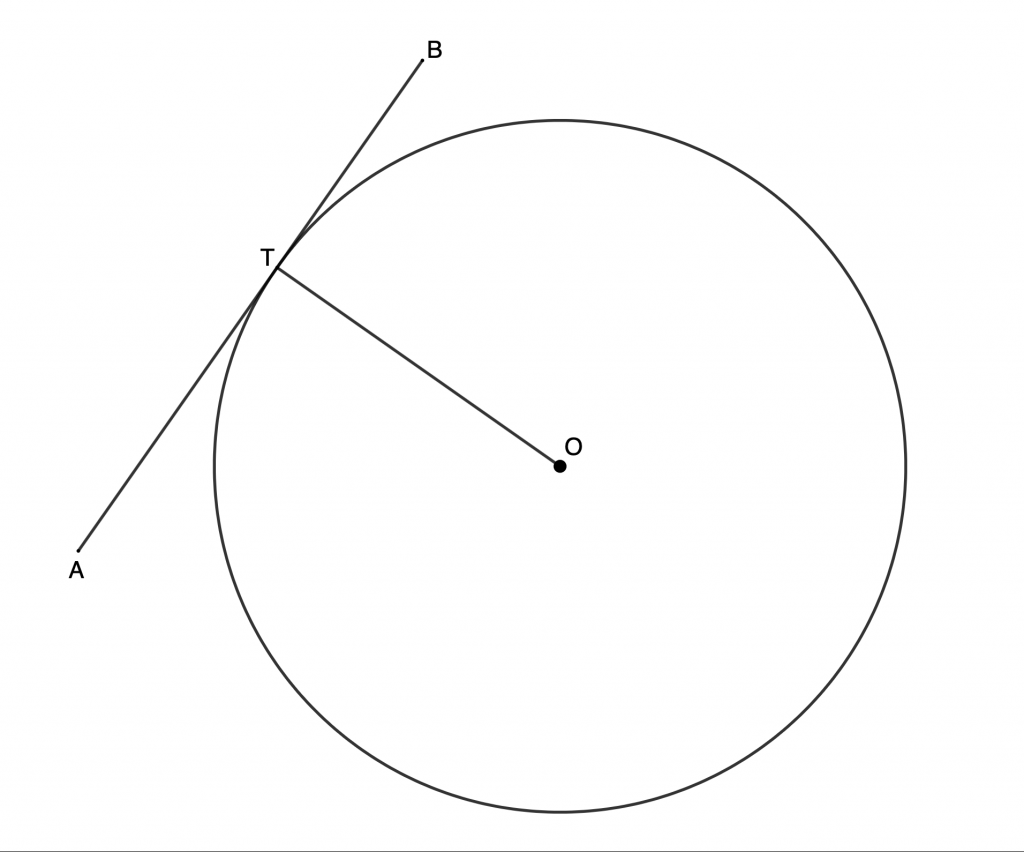
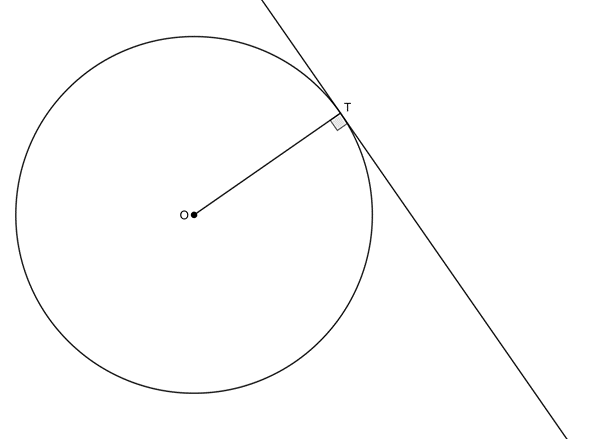
We already know that the radius of a circle is perpendicular to a tangent at the point of contact (the point of tangency) (figure 1). This will be our first theorem in this unit.
You do not need to be able to prove any of the tangent to circle theorems yourself. You can simply assume that they are true. The following sections explain the theorems that you need to be able to state and use. Note that they are numbered only for reference purposes and continue the numbering from unit 3. These theorems do not have official numbers.
Theorem 7
This theorem covers what you’ve already learnt about radii and tangents to circles.
Theorem 7: The radius of a circle is perpendicular to the tangent at the point of tangency
If a tangent is drawn to a circle, then it is perpendicular to the radius at the point of contact.
The tangent [latex]\scriptsize AT[/latex] is perpendicular to the radius [latex]\scriptsize OT[/latex] at point [latex]\scriptsize T[/latex].
Reason: radius [latex]\scriptsize \bot[/latex] tangent
Now let’s look at the converse to this theorem.
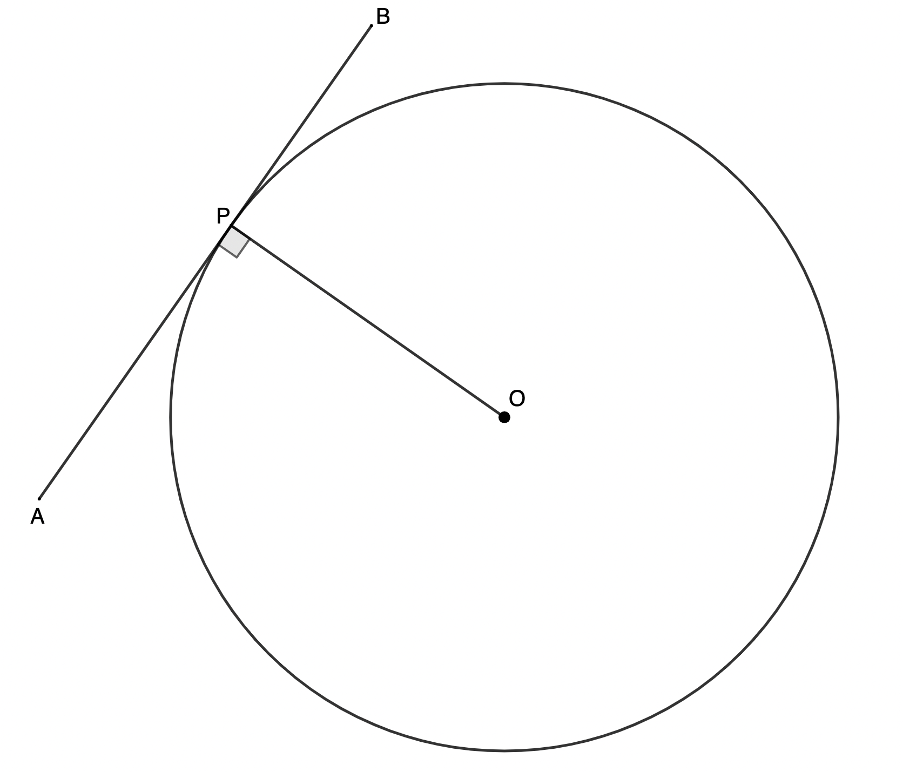
Converse to theorem 7: If a line is perpendicular to a radius at a point on the circumference of a circle, then it is a tangent to the circle
If a line is drawn perpendicular to a radius at the point where the radius meets the circle, then it is a tangent to the circle at that point.
If line [latex]\scriptsize AB[/latex] is perpendicular to radius [latex]\scriptsize OP[/latex] at point [latex]\scriptsize P[/latex], then [latex]\scriptsize AB[/latex] is a tangent to the circle at [latex]\scriptsize P[/latex].
Reason: radius [latex]\scriptsize \bot[/latex] line at point of contact
Example 4.1
[latex]\scriptsize AB[/latex] is a tangent to circle centre [latex]\scriptsize O[/latex] at [latex]\scriptsize E[/latex]. [latex]\scriptsize C[/latex] is a point on [latex]\scriptsize AO[/latex] on the circumference of the circle. [latex]\scriptsize AC=9[/latex] and [latex]\scriptsize AE=15[/latex]. Determine the length of the radius of the circle.
Solution
[latex]\scriptsize \begin{align*}O\hat{E}A & ={{90}^\circ}\quad \text{(radius }\bot \text{ tangent)}\\\therefore A{{O}^{2}} & =O{{E}^{2}}+A{{E}^{2}}\quad \text{(Pythagoras)}\\\text{Let }OE & =x\\\therefore AO & =9+x\\\therefore {{(9+x)}^{2}} & ={{x}^{2}}+{{15}^{2}}\\\therefore 81+18x+{{x}^{2}} & ={{x}^{2}}+225\\\therefore 18x & =144\\\therefore x & =\displaystyle \frac{{144}}{{18}}\\ & =8\end{align*}[/latex]
Theorem 8
This next theorem looks at two tangents to a circle from the same point.
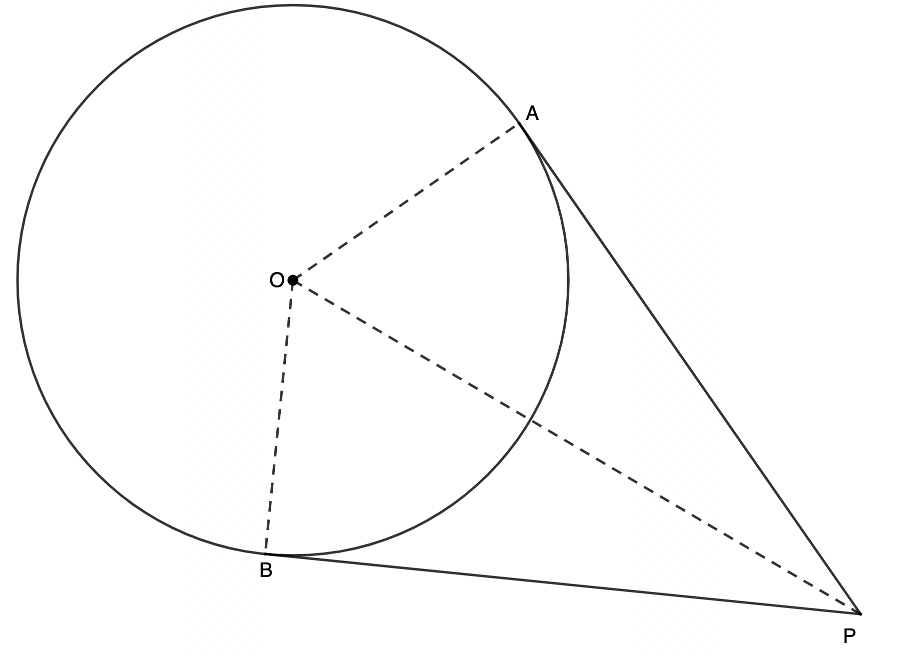
Theorem 8: Two tangents from the same point outside a circle
If two tangents are drawn from the same point outside a circle, then they are equal in length.
If tangents [latex]\scriptsize PA[/latex] and [latex]\scriptsize PB[/latex] are drawn from the same point [latex]\scriptsize P[/latex], then [latex]\scriptsize PA=PB[/latex].
Reason: tangents from same point are equal
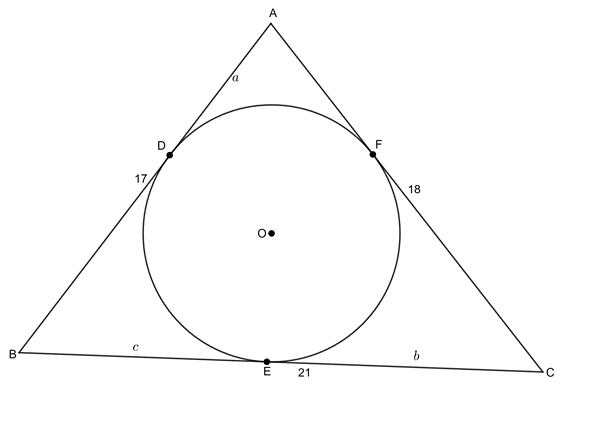
Example 4.2
[latex]\scriptsize AB=17[/latex], [latex]\scriptsize AC=18[/latex] and [latex]\scriptsize BC=21[/latex]. [latex]\scriptsize AB[/latex] is a tangent at [latex]\scriptsize D[/latex]. [latex]\scriptsize AC[/latex] is a tangent at [latex]\scriptsize \displaystyle F[/latex]. [latex]\scriptsize BC[/latex] is a tangent at [latex]\scriptsize E[/latex]. Determine the lengths of [latex]\scriptsize a[/latex], [latex]\scriptsize b[/latex] and [latex]\scriptsize c[/latex].
Solution
[latex]\scriptsize \begin{align*}AD&=AF=a\quad (\text{tangents from same point =)}\\CF&=CE=b\quad (\text{tangents from same point =)}\\BE&=BD=c\quad (\text{tangents from same point =)}\\&\text{But}\\AD+BD&=17\quad \text{(given)}\\\therefore a+c&=17\quad (1)\\AF+CF&=18\quad \text{(given)}\\\therefore a+b&=18\quad (2)\\CE+BE&=21\quad \text{(given)}\\\therefore b+c&=21\quad (3)\end{align*}[/latex]
We have three equations that we can solve simultaneously.
Subtract [latex]\scriptsize (2)[/latex] from [latex]\scriptsize (1)[/latex]:
[latex]\scriptsize \begin{align*}c-b=-1\\\therefore c=b-1\quad (4)\end{align*}[/latex]
Substitute [latex]\scriptsize (4)[/latex] into [latex]\scriptsize (3)[/latex]:
[latex]\scriptsize \begin{align*}b+(b-1) & =21\\\therefore 2b & =22\\\therefore b & =11\end{align*}[/latex]
Substitute [latex]\scriptsize b=11[/latex] into [latex]\scriptsize (4)[/latex]:
[latex]\scriptsize c=11-1=10[/latex]
Substitute [latex]\scriptsize c=10[/latex] into [latex]\scriptsize (1)[/latex]:
[latex]\scriptsize \begin{align*}a+10 & =17\\\therefore a & =7\end{align*}[/latex]
Theorem 9
Let’s now look at the tan-chord theorem.
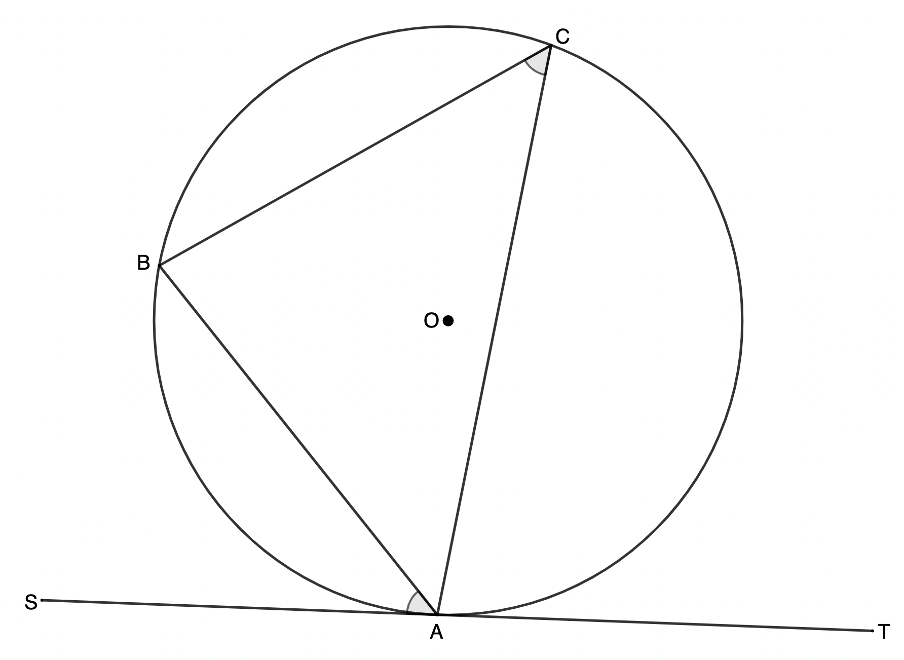
Theorem 9: Tan-chord theorem
The angle between a tangent to a circle and a chord drawn at the point of contact, is equal to the angle which the chord subtends in the alternate segment.
If [latex]\scriptsize ST[/latex] is a tangent to the circle at [latex]\scriptsize A[/latex], then [latex]\scriptsize S\hat{A}B[/latex] (the angle between the tangent and the chord) is equal to [latex]\scriptsize A\hat{C}B[/latex] (the angle subtended by the chord in the alternate segment).
Reason: tan. chord theorem
Note: The chord must meet the circumference at the point of tangency. The angle subtended by the chord must be in the alternate segment of the circle (i.e. not the segment nearest to the tangent).
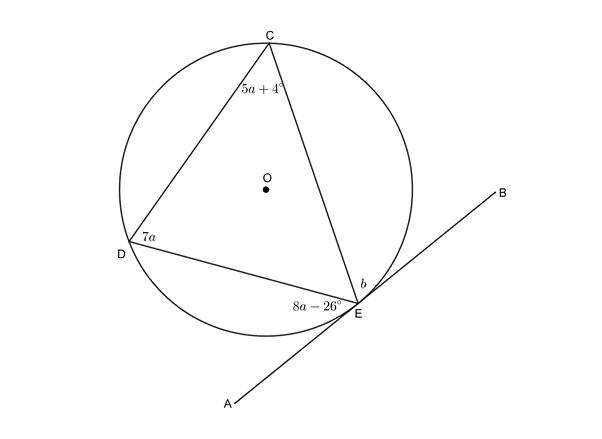
Example 4.3
[latex]\scriptsize AB[/latex] is a tangent to the circle at [latex]\scriptsize E[/latex]. Determine the values of [latex]\scriptsize a[/latex] and [latex]\scriptsize b[/latex].
Solution
[latex]\scriptsize \begin{align*}A\hat{E}D & =D\hat{C}E\quad \text{(tan}\text{. chord theorem)}\\\therefore 8a-{{26}^\circ} & =5a+{{4}^\circ}\\\therefore 3a & ={{30}^\circ}\\\therefore a & ={{10}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}B\hat{E}C & =E\hat{D}C\quad \text{(tan}\text{. chord theorem)}\\\therefore b & =7a=7\times {{10}^\circ}={{70}^\circ}\end{align*}[/latex]
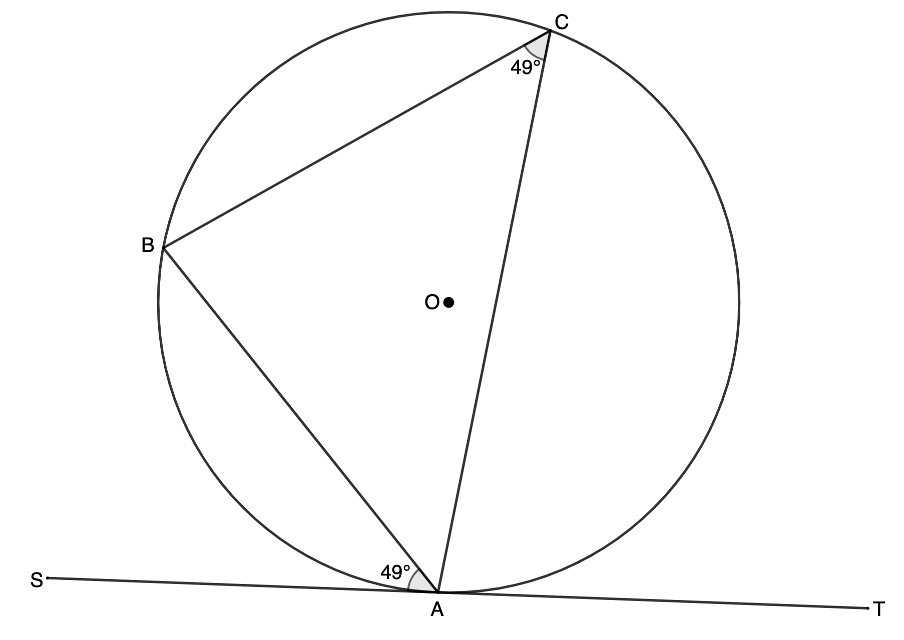
Converse to theorem 9: Angle in opposite segment equal
We can prove that a line is a tangent to a circle at a point if we can show that the angle between the line and a chord drawn from that point on the line is equal to the angle subtended by the chord in the alternate segment.
If [latex]\scriptsize S\hat{A}B[/latex] (the angle between the line and the chord) is equal to [latex]\scriptsize A\hat{C}B[/latex] (the angle subtended by the chord in the alternate segment), then [latex]\scriptsize ST[/latex] is a tangent to circle [latex]\scriptsize ABC[/latex] at [latex]\scriptsize A[/latex].
Reason: [latex]\scriptsize \angle[/latex] between tangent and chord [latex]\scriptsize =\angle[/latex] in opp seg
Exercise 4.1
- Determine the value of the unknown lengths:
- Determine the size of the unknown angles:
- Given [latex]\scriptsize EC=ED[/latex], [latex]\scriptsize AB\parallel CD[/latex] and [latex]\scriptsize \displaystyle {{\hat{E}}_{2}}={{\hat{D}}_{1}}[/latex]. Prove:

- [latex]\scriptsize AEB[/latex] is a tangent to circle [latex]\scriptsize CDE[/latex].
- [latex]\scriptsize DE[/latex] is a tangent to the circle [latex]\scriptsize EFB[/latex].
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- That the tangent to a circle is perpendicular to the radius at point of contact.
- That if a line is perpendicular to a radius, then the line is a tangent to the circle at that point.
- That two tangents drawn from the same point outside a circle are equal in length.
- That the angle between a tangent to a circle and a chord draw from the point of contact is equal to the angle subtended by the chord in the alternate segment.
- That if the angle between a line and a chord drawn from the line is equal to the angle the chord subtends in the alternate segment, then the line is a tangent to the circle at that point.
Unit 4: Assessment
Suggested time to complete: 35 minutes
Question 1 adapted from NC(V) Mathematics Level 4 November 2011 question 1.3
- Given below is a circle with a cyclic quadrilateral [latex]\scriptsize ABCD[/latex] and [latex]\scriptsize EF[/latex] a tangent at [latex]\scriptsize A[/latex]. [latex]\scriptsize EF\parallel BC[/latex]and [latex]\scriptsize \hat{F}={{55}^\circ}[/latex]. [latex]\scriptsize A\hat{B}D={{25}^\circ}[/latex].

Calculate, with reasons, the magnitudes of the following angles:- [latex]\scriptsize D\hat{A}F[/latex]
- [latex]\scriptsize F\hat{D}A[/latex]
- [latex]\scriptsize {{\hat{D}}_{2}}[/latex]
- [latex]\scriptsize {{\hat{A}}_{2}}[/latex]
- [latex]\scriptsize \hat{C}[/latex]
- [latex]\scriptsize {{\hat{B}}_{1}}[/latex]
Question 2 adapted from NC(V) Mathematics Level 4 November 2013 question 1.4
- In the figure, [latex]\scriptsize O[/latex] is the centre of the circle. [latex]\scriptsize P[/latex], [latex]\scriptsize Q[/latex], [latex]\scriptsize R[/latex] and [latex]\scriptsize S[/latex] are points on the circumference of the circle. [latex]\scriptsize PR[/latex] is a diameter of the circle and [latex]\scriptsize MRT[/latex] is a tangent at [latex]\scriptsize R[/latex]. [latex]\scriptsize {{\hat{S}}_{2}}={{61}^\circ}[/latex] and [latex]\scriptsize {{\hat{R}}_{3}}={{52}^\circ}[/latex].
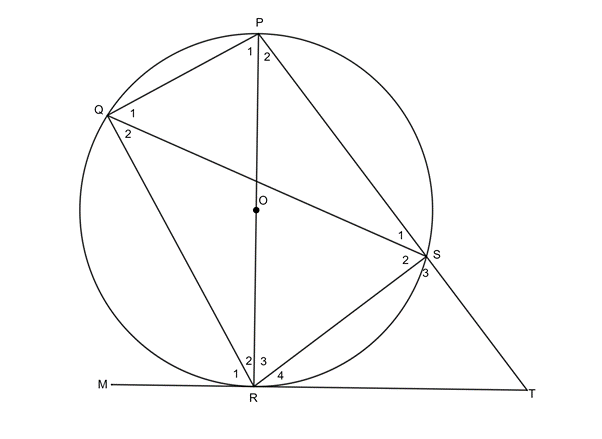
Determine, with reasons, the sizes of:- [latex]\scriptsize {{\hat{R}}_{1}}[/latex]
- [latex]\scriptsize {{\hat{R}}_{4}}[/latex]
- [latex]\scriptsize {{\hat{S}}_{3}}[/latex]
Question 3 adapted from NC(V) Mathematics Level 4 November 2015 question 1.2
Question 4 adapted from NC(V) Mathematics Level 4 November 2012 question 1.3
- In the following figure, [latex]\scriptsize ABCD[/latex] is a cyclic quadrilateral. [latex]\scriptsize DC[/latex] is a tangent to a circle through [latex]\scriptsize B[/latex], [latex]\scriptsize C[/latex] and [latex]\scriptsize T[/latex]. [latex]\scriptsize AC[/latex] passes through [latex]\scriptsize T[/latex] on the circle. [latex]\scriptsize DC[/latex] is produced to [latex]\scriptsize S[/latex] and [latex]\scriptsize TB[/latex] is joined.
Let [latex]\scriptsize B\hat{C}S=x[/latex] and [latex]\scriptsize B\hat{A}C=y[/latex].
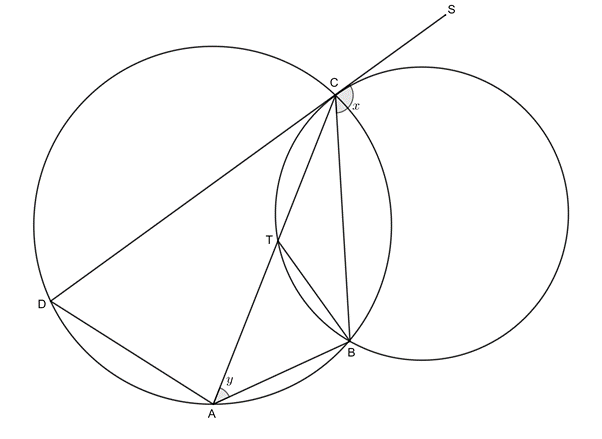
- Name, giving reasons, TWO other angles that are equal to [latex]\scriptsize x[/latex].
- Determine, giving reasons, the value of [latex]\scriptsize A\hat{B}T[/latex] in terms of [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex].
- Hence, prove that [latex]\scriptsize DA[/latex] is a tangent to circle [latex]\scriptsize ABT[/latex].
The full solutions are at the end of the unit.
Unit 4: Solutions
Exercise 4.1
- .
- .
[latex]\scriptsize \begin{align*}O\hat{P}D & ={{90}^\circ}\quad \text{(radius }\bot \text{ tangent)}\\DT & =DP=6\quad \text{(tangents from same point equal)}\\{{d}^{2}} & =O{{P}^{2}}+D{{P}^{2}}\quad \text{(Pythagoras)}\\\therefore {{d}^{2}} & =25+36=61\\\therefore d & =\sqrt{{61}}\end{align*}[/latex] - [latex]\scriptsize DB=13\quad \text{(given)}[/latex]
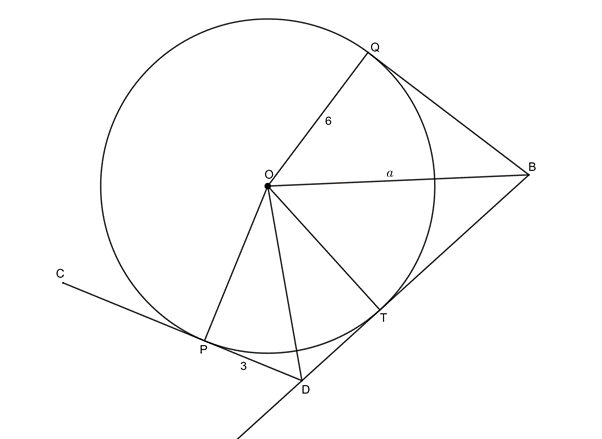
[latex]\scriptsize \begin{align*}PD & =DT=3\quad \text{(tangents from same point equal)}\\\therefore TB & =13-3=10\end{align*}[/latex]
[latex]\scriptsize TB=QB=10\quad \text{(tangents from same point equal)}[/latex]
[latex]\scriptsize \begin{align*}O\hat{Q}B & ={{90}^\circ}\quad \text{(radius }\bot \text{ tangent)}\\\therefore {{a}^{2}} & ={{6}^{2}}+{{10}^{2}}=136\\\therefore a & =2\sqrt{{34}}\end{align*}[/latex]
- .
- .
- [latex]\scriptsize a={{27}^\circ}\quad \text{(tan}\text{. chord theorem)}[/latex]
- .
[latex]\scriptsize \begin{align*}P\hat{D}C & ={{48}^\circ}\quad \text{(tan}\text{. chord theorem)}\\P\hat{D}C & =P\hat{C}D\quad \text{(isosc }\Delta )\\\therefore a & ={{48}^\circ}\end{align*}[/latex]
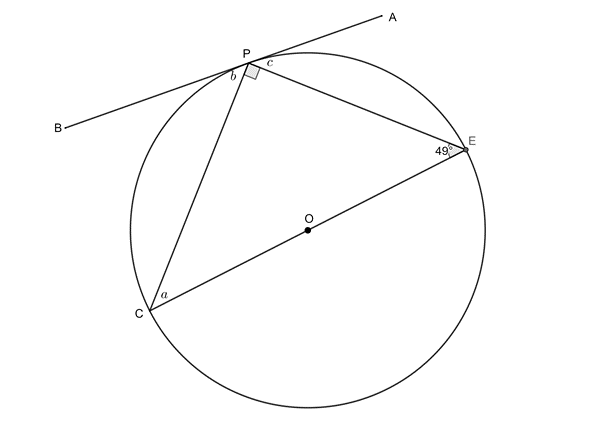
[latex]\scriptsize \begin{align*}A\hat{P}D & ={{48}^\circ}\quad \text{(tan}\text{. chord theorem)}\\b & ={{180}^\circ}-{{48}^\circ}-{{48}^\circ}\quad \text{(}\angle \text{s on str line suppl)}\\\therefore b & ={{84}^\circ}\end{align*}[/latex] - [latex]\scriptsize a={{180}^\circ}-{{90}^\circ}-{{49}^\circ}={{41}^\circ}\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}[/latex]
[latex]\scriptsize b={{49}^\circ}\quad \text{(tan}\text{. chord theorem)}[/latex]
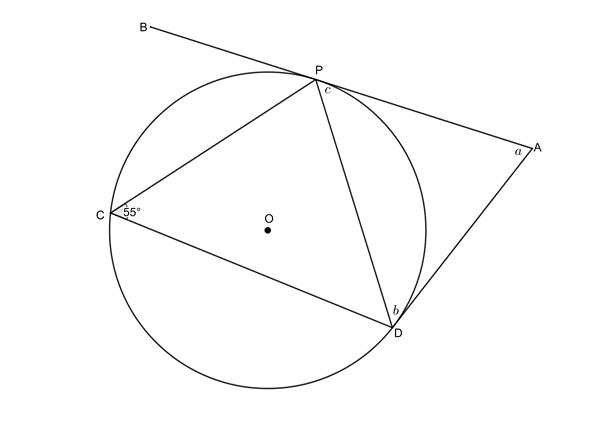
[latex]\scriptsize c={{41}^\circ}\quad \text{(tan}\text{. chord theorem)}[/latex] - [latex]\scriptsize c={{55}^\circ}\quad \text{(tan}\text{. chord theorem)}[/latex]
[latex]\scriptsize b={{55}^\circ}\quad \text{(tan}\text{. chord theorem)}[/latex]
[latex]\scriptsize a={{180}^\circ}-{{55}^\circ}-{{55}^\circ}={{70}^\circ}\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}[/latex]
- .
- .
[latex]\scriptsize \begin{align*}{{{\hat{E}}}_{1}} & =D\hat{C}E\quad \text{(alt }\angle \text{s }=;\text{ }AB\parallel CD\text{)}\\D\hat{C}E & ={{{\hat{D}}}_{{1+2}}}=C\hat{D}E\quad \text{(isosc }\Delta \text{)}\\\therefore {{{\hat{E}}}_{1}} & =C\hat{D}E\\\therefore AEB\text{ } & \text{is a tangent to circle }CDE\quad \text{(}\angle \text{ between tangent and chord = }\angle \text{ in opp seg)}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}{{{\hat{E}}}_{2}} & ={{{\hat{D}}}_{1}}\quad \text{(given)}\\E\hat{B}F & ={{{\hat{D}}}_{1}}\quad (\text{alt }\angle \text{s }=;\text{ }AB\parallel CD\text{)}\\\therefore E\hat{B}F & ={{{\hat{E}}}_{2}}\\\therefore DE\text{ } & \text{is a tangent to circle EFB}\quad \text{(}\angle \text{ between tangent and chord = }\angle \text{ in opp seg)}\end{align*}[/latex]
- .
Unit 4: Assessment
- .
- [latex]\scriptsize D\hat{A}F={{25}^\circ}\quad \text{(tan}\text{. chord theorem)}[/latex]
- .
[latex]\scriptsize \begin{align*}F\hat{D}A&={{180}^\circ}-A\hat{F}D-D\hat{A}F\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\&={{180}^\circ}-{{55}^\circ}-{{25}^\circ}\\&={{100}^\circ}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{{\hat{D}}}_{2}}&={{180}^\circ}-F\hat{D}A\quad \text{(}\angle \text{s on str lin suppl)}\\&=18{{\text{0}}^\circ}-{{100}^\circ}\\&={{80}^\circ}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{{\hat{A}}}_{2}}&={{180}^\circ}-A\hat{B}D-{{{\hat{D}}}_{2}}\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\&=18{{\text{0}}^\circ}-{{25}^\circ}-{{80}^\circ}\\&={{75}^\circ}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\hat{C}&={{180}^\circ}-{{{\hat{A}}}_{2}}\quad \text{(opp }\angle \text{s of cyclic quad suppl)}\\&=18{{\text{0}}^\circ}-{{75}^\circ}\\&={{105}^\circ}\end{align*}[/latex] - [latex]\scriptsize {{\hat{B}}_{1}}=\hat{F}={{55}^\circ}\quad \text{(alt }\angle \text{s }=;\text{ }EF\parallel BC\text{)}[/latex]
- .
- [latex]\scriptsize \displaystyle {{\hat{R}}_{1}}={{S}_{2}}={{61}^\circ}\quad (\tan .\text{ chord theorem)}[/latex]
- .
[latex]\scriptsize \displaystyle \begin{align*}{{{\hat{R}}}_{3}} & ={{{\hat{Q}}}_{1}}={{52}^\circ}\quad \text{(}\angle \text{s in same seg)}\\{{{\hat{Q}}}_{1}}+{{{\hat{Q}}}_{2}} & ={{90}^\circ}\quad (\angle \text{s in semi-circle)}\\\therefore {{{\hat{Q}}}_{2}} & ={{38}^\circ}\\{{R}_{4}} & ={{{\hat{Q}}}_{2}}={{38}^\circ}\quad \text{(tan}\text{. chord theorem)}\end{align*}[/latex] - [latex]\scriptsize {{\hat{S}}_{3}}={{\hat{Q}}_{{1+2}}}={{90}^\circ}\quad \text{(ext }\angle \text{ = opp int }\angle \text{ in cyclic quad)}[/latex]
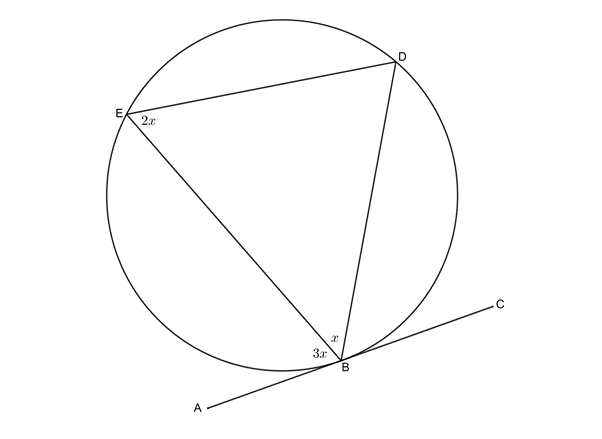
- .
[latex]\scriptsize \begin{align*}C\hat{B}D & =B\hat{E}D=2x\quad \text{(tan}\text{. chord theorem)}\\A\hat{B}E+E\hat{B}D+C\hat{B}D & ={{180}^\circ}\quad \text{(}\angle \text{s on str line suppl)}\\\therefore 3x+x+2x & ={{180}^\circ}\\\therefore 6x & ={{180}^\circ}\\\therefore x & ={{30}^\circ}\end{align*}[/latex] - .
- [latex]\scriptsize C\hat{T}B=x\quad \text{(tan}\text{. chord theorem)}[/latex]
[latex]\scriptsize B\hat{A}D=x\quad \text{(ext }\angle \text{ = opp int }\angle \text{ in cyclic quad)}[/latex] - .
[latex]\scriptsize \begin{align*}A\hat{T}B & =180-C\hat{T}B\quad \text{(}\angle \text{s on str line suppl)}\\\therefore A\hat{T}B & ={{180}^\circ}-x\\A\hat{B}T & ={{180}^\circ}-A\hat{T}B-B\hat{A}T\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\\therefore A\hat{B}T & ={{180}^\circ}-({{180}^\circ}-x)-y\\ & =x-y\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}B\hat{A}D & =x\quad \text{(proven in a}\text{.)}\\\therefore C\hat{A}D & =x-y\\\therefore C\hat{A}D & =A\hat{B}T\end{align*}[/latex]
Therefore, [latex]\scriptsize DA[/latex] is a tangent to circle [latex]\scriptsize ABT[/latex] ([latex]\scriptsize \angle[/latex] between tangent and chord [latex]\scriptsize =\angle[/latex] in opp seg).
- [latex]\scriptsize C\hat{T}B=x\quad \text{(tan}\text{. chord theorem)}[/latex]
Media Attributions
- figure1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- theorem7 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- theorem7converse © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example4.1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- theorem8 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example4.2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- theorem9 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example4.3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- theorem9converse © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise4.1 Q1a © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise4.1 Q1b © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise4.1 Q2a © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise4.1 Q2b © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise4.1 Q2c © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise4.1 Q2d © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise4.1 Q3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license