Unit 3 outcomes

By the end of this unit you will be able to:

• Define a cyclic quadrilateral.
• Apply the theorem opposite angles of a cyclic quadrilateral are supplementary.
• Apply the theorem exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
• Apply the converses of equality between opposite angles, between angles in the same segment, and between exterior angles and interior opposite angles, to prove a quadrilateral is cyclic.

What you should know

Before you start this unit, make sure you can:

1. State and use all the circle theorems covered in unit 2:
   1. A line drawn perpendicular to a chord from the centre of the circle bisects the chord.
   2. A line drawn from the circle centre to the mid-point of chord is perpendicular to the chord.
   3. The angle subtended by an arc or chord at the centre of a circle is twice the size of the angle subtended at the circumference.
   4. The diameter of a circle subtends a right angle at the circumference.
   5. If an angle subtended by a chord at a point on the circumference is a right angle, then the chord is a diameter.
   6. Angles subtended by the same arc or chord in the same segment of a circle (on the same side of the chord) are equal.

Introduction

A quadrilateral is any flat four-sided figure. Each of the four sides must be straight. A square is an example of a quadrilateral, as is a parallelogram. These are very special kinds of quadrilaterals with special properties.

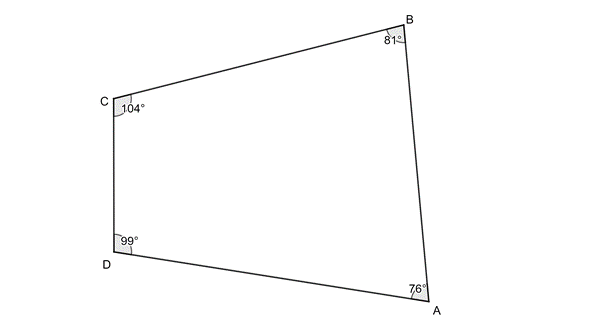
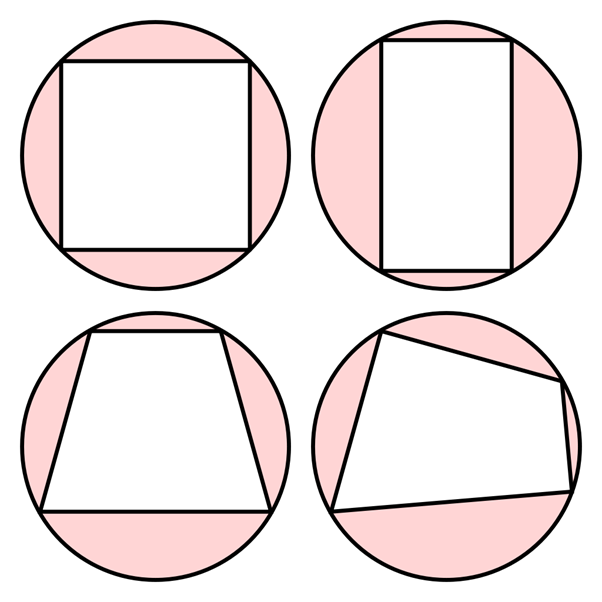
Most quadrilaterals have no special characteristics other than that they have four straight sides and, therefore, four interior angles. We call these irregular quadrilaterals. Figure 1 shows various examples of quadrilaterals.

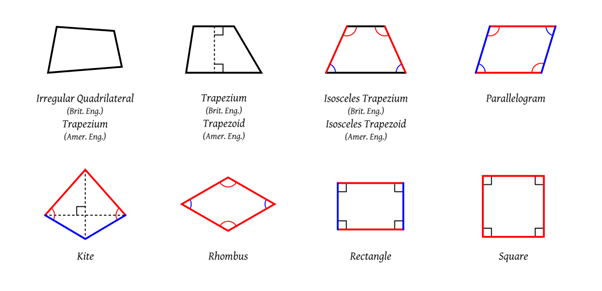
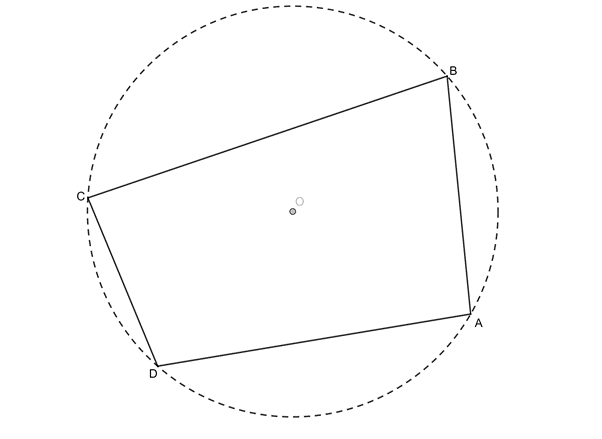
But some quadrilaterals are just the right shape that their four corners all lie on the circumference of the same circle. These are called cyclic quadrilaterals (see figure 2). Some special quadrilaterals such as squares, rectangles and parallelograms are always cyclic but many irregular quadrilaterals are cyclic as well.

Take note!

For a quadrilateral to be cyclic, all four vertices (corners) of the quadrilateral must lie on the circumference of the same circle.

Cyclic quadrilateral theorems

You do not need to be able to prove any of the cyclic quadrilateral theorems yourself. You can simply assume that they are true. The following sections explain the theorems that you need to be able to state and use. Note that they are numbered only for reference purposes and continue the numbering from unit 2. These theorems do not have official numbers.

Theorem 5

Let’s look at the theorem involving opposite angles of a cyclic quadrilateral.

Example 3.1

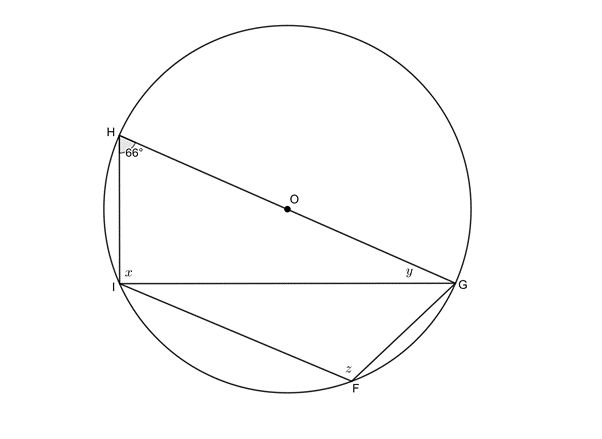
Given the circle with centre [latex]\scriptsize O[/latex] with diameter [latex]\scriptsize GH[/latex]and cyclic quadrilateral [latex]\scriptsize FGHI[/latex]. [latex]\scriptsize GI[/latex] is drawn and [latex]\scriptsize G\hat{H}I={{66}^\circ}[/latex]. Determine the values of [latex]\scriptsize x[/latex], [latex]\scriptsize y[/latex] and [latex]\scriptsize z[/latex].

Solution

[latex]\scriptsize x={{90}^\circ}\quad \text{(}\angle \text{s in semi-circle)}[/latex]
[latex]\scriptsize y={{180}^\circ}-{{66}^\circ}-{{90}^\circ}={{24}^\circ}\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}[/latex]
[latex]\scriptsize z={{180}^\circ}-{{66}^\circ}={{114}^\circ}\quad \text{(}\angle \text{s in cyclic quad)}[/latex]

Theorem 6

The next theorem looks at exterior angles.

Example 3.2

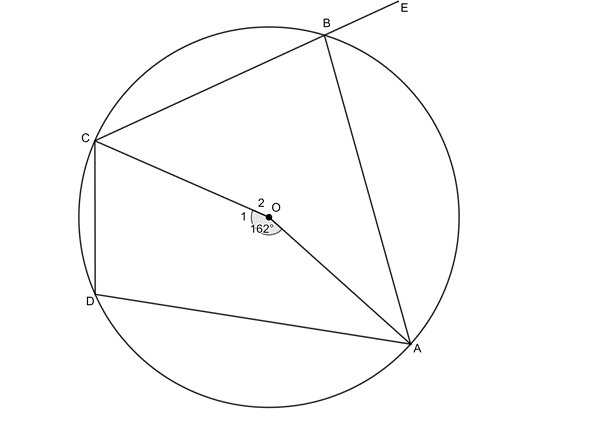
Given the circle with centre [latex]\scriptsize O[/latex] and cyclic quadrilateral [latex]\scriptsize ABCD[/latex], and [latex]\scriptsize \displaystyle {{\hat{O}}_{1}}={{162}^\circ}[/latex]. Determine the value the value of [latex]\scriptsize A\hat{B}E[/latex].

Solution

[latex]\scriptsize \begin{align*}{{{\hat{O}}}_{2}} & ={{360}^\circ}-{{162}^\circ}={{198}^\circ}\quad \text{(}\angle \text{ around a point)}\\\therefore \hat{D} & ={{99}^\circ}\quad \text{(}\angle \text{ at centre =2}\angle \text{ at circumference)}\\\therefore A\hat{B}E & ={{99}^\circ}\quad \text{(ext }\angle \text{= opp int }\angle \text{ in cyclic quad)}\end{align*}[/latex]

Proving a quadrilateral is a cyclic quadrilateral

So far, we have seen two ways in which we can prove that a quadrilateral is a cyclic quadrilateral.

• If we can prove that the opposite interior angles of the quadrilateral are supplementary, then the quadrilateral is cyclic.
• If we can prove that the exterior angle of the quadrilateral is equal to the opposite interior angle, then the quadrilateral is cyclic.

But there is a third way. Remember theorem 4 from unit 2? It stated that if the angles subtended by a chord of the circle are on the same side of the chord, then the angles are equal.

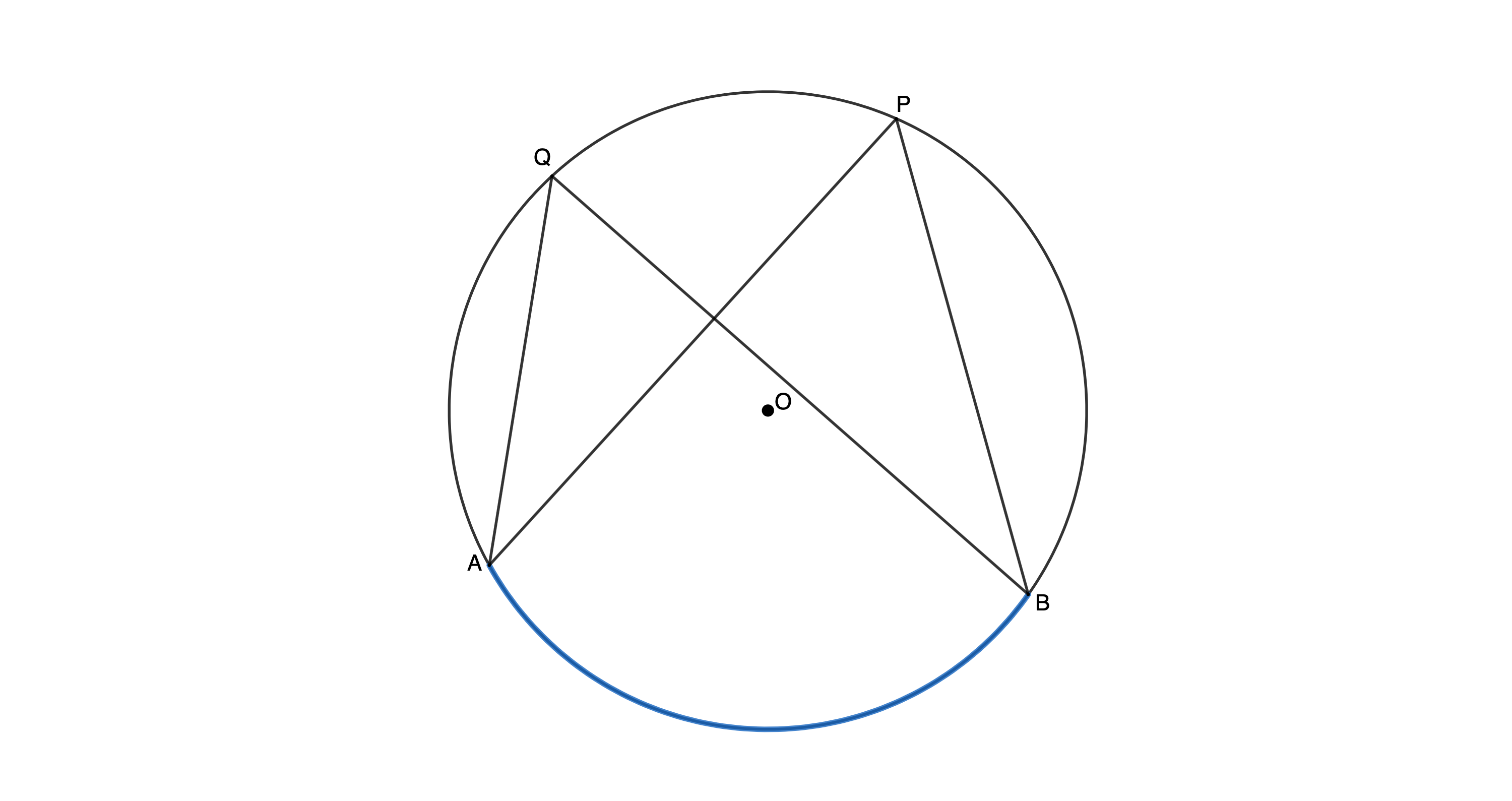
Because [latex]\scriptsize \hat{Q}[/latex] and [latex]\scriptsize \hat{P}[/latex] are both subtended by arc [latex]\scriptsize AB[/latex] (or chord [latex]\scriptsize AB[/latex]), then we know that [latex]\scriptsize \hat{Q}=\hat{P}[/latex]. But now have a look at [latex]\scriptsize ABPQ[/latex]. Can you see that all four vertices lie on the circumference of the same circle? Therefore, it is a cyclic quadrilateral.

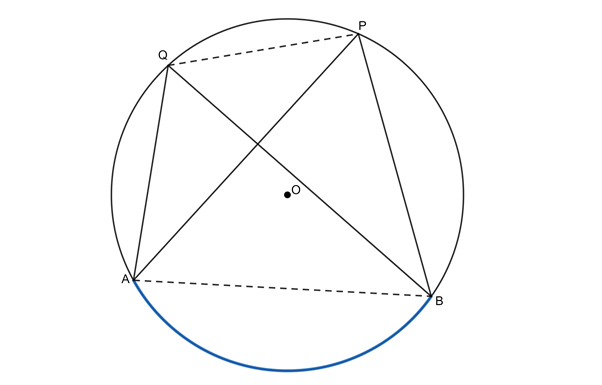
This means that we can use the converse of theorem 4 to prove that a quadrilateral is cyclic. If the angles in the same segment of a circle are equal, then the quadrilateral made by the chord and the two angles must be a cyclic quadrilateral.

Take note!

There are three ways to prove that a quadrilateral is a cyclic quadrilateral:

Proof 1: Opp int [latex]\scriptsize \angle[/latex]s suppl

If [latex]\scriptsize \hat{A}+\hat{C}={{180}^\circ}[/latex] or [latex]\scriptsize \hat{B}+\hat{D}={{180}^\circ}[/latex], then [latex]\scriptsize ABCD[/latex] is a cyclic quadrilateral.

Proof 2: ext [latex]\scriptsize \angle =[/latex]opp int [latex]\scriptsize \angle[/latex]

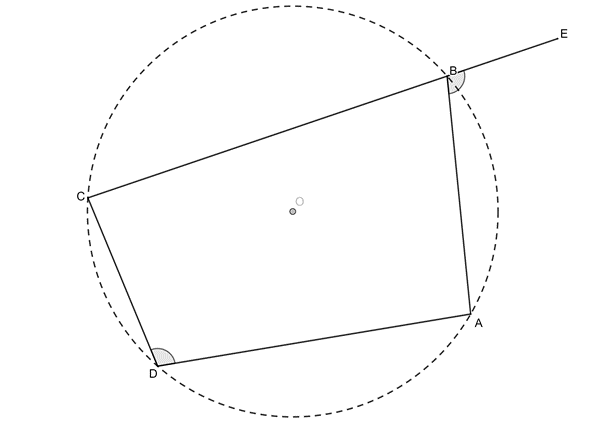
If [latex]\scriptsize A\hat{B}E=\hat{D}[/latex], then [latex]\scriptsize ABCD[/latex] is a cyclic quadrilateral.

Proof 3: [latex]\scriptsize \angle[/latex]s in same segment

If [latex]\scriptsize A\hat{C}D=A\hat{B}D[/latex], then [latex]\scriptsize ABCD[/latex] is a cyclic quadrilateral.

Example 3.3

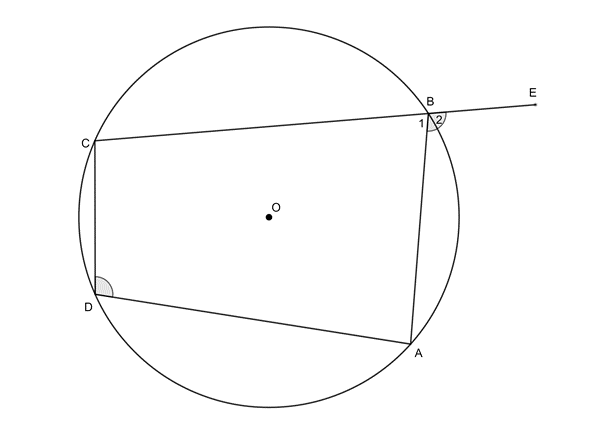
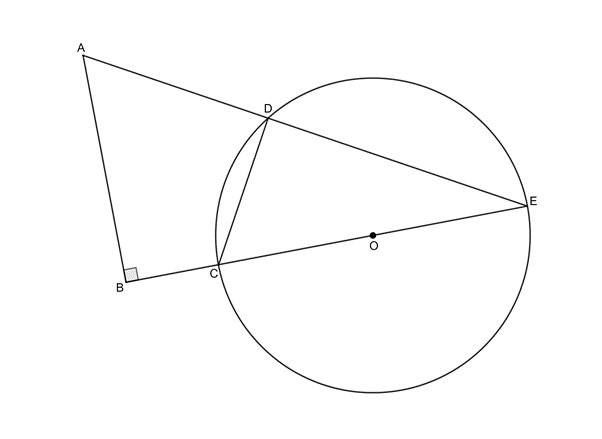
If [latex]\scriptsize COE[/latex] is a diameter of circle centre [latex]\scriptsize O[/latex], prove that [latex]\scriptsize ABCD[/latex] is a cyclic quadrilateral.

Solution

[latex]\scriptsize \begin{align*}C\hat{D}E & ={{90}^\circ}\quad \text{(}\angle \text{s in semi-circle)}\\\therefore C\hat{D}E & =A\hat{B}C={{90}^\circ}\end{align*}[/latex]
Therefore [latex]\scriptsize ABCD[/latex] is a cyclic quadrilateral (ext [latex]\scriptsize \angle =[/latex]opp int [latex]\scriptsize \angle[/latex]).

Exercise 3.1

1. Find the value of the unknown angles:
   1. .
      
   2. .
      
   3. .
      
2. In each case, determine if [latex]\scriptsize ABCD[/latex] is a cyclic quadrilateral:
   1. .
      
   2. .
      

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• That a cyclic quadrilateral is any four-sided shape whose vertices all lie on the circumference of the same circle.
• The opposite angles of a cyclic quadrilateral are supplementary.
• The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
• A quadrilateral can be proven to be a cyclic quadrilateral if you can show that:
  • the opposite angles are supplementary
  • the exterior angle is equal to the interior opposite angle
  • the angles subtended by one side of the quadrilateral are equal.

Unit 3: Assessment

Suggested time to complete: 25 minutes

1. [latex]\scriptsize O[/latex] is the centre of the circle with diameter [latex]\scriptsize AB[/latex]. [latex]\scriptsize CD\bot AB[/latex] at [latex]\scriptsize P[/latex] and chord [latex]\scriptsize DE[/latex]cuts [latex]\scriptsize AB[/latex] at [latex]\scriptsize F[/latex]. [latex]\scriptsize CB=DB[/latex].
   
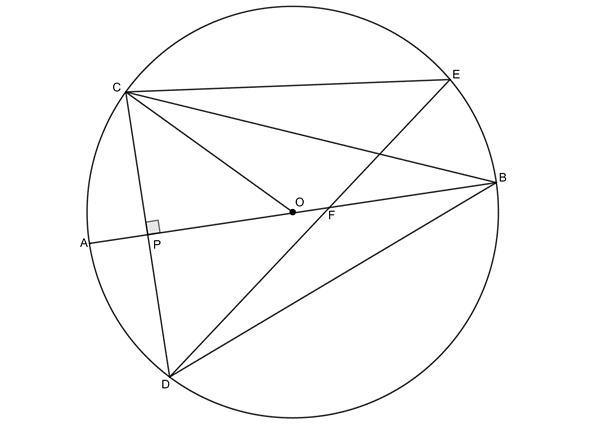
   Prove that:
   1. [latex]\scriptsize C\hat{B}P=D\hat{B}P[/latex]
   2. [latex]\scriptsize C\hat{E}D=2\times C\hat{B}A[/latex]
   3. [latex]\scriptsize A\hat{B}D=\displaystyle \frac{1}{2}C\hat{O}A[/latex]
2. [latex]\scriptsize A[/latex], [latex]\scriptsize B[/latex], [latex]\scriptsize C[/latex] and [latex]\scriptsize D[/latex] are points on circle centre [latex]\scriptsize O[/latex]. [latex]\scriptsize A\hat{B}C={{69}^\circ}[/latex]. [latex]\scriptsize AD[/latex] and [latex]\scriptsize BC[/latex] are extended to meet at [latex]\scriptsize E[/latex]. [latex]\scriptsize AB=AC[/latex].
   
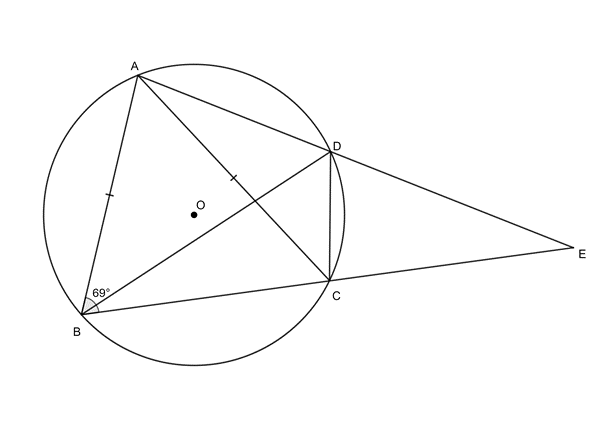
   1. Determine, with reasons, two more angles equal to [latex]\scriptsize A\hat{B}C[/latex].
   2. If [latex]\scriptsize B\hat{A}D={{82}^\circ}[/latex], calculate [latex]\scriptsize B\hat{C}D[/latex], [latex]\scriptsize C\hat{E}D[/latex] and [latex]\scriptsize A\hat{B}D[/latex].

The full solutions are at the end of the unit.

Unit 3: Solutions

Exercise 3.1

1. .
   1. .
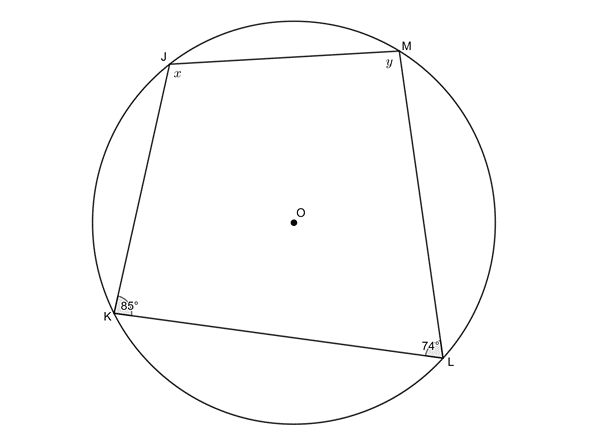
      [latex]\scriptsize \begin{align*}x&={{180}^\circ}-{{74}^\circ}\quad \text{(opp }\angle \text{s in cyclic quad)}\\&=10{{\text{6}}^\circ}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}y&={{180}^\circ}-{{85}^\circ}\quad \text{(opp }\angle \text{s in cyclic quad)}\\&=9{{\text{5}}^\circ}\end{align*}[/latex]
   2. .
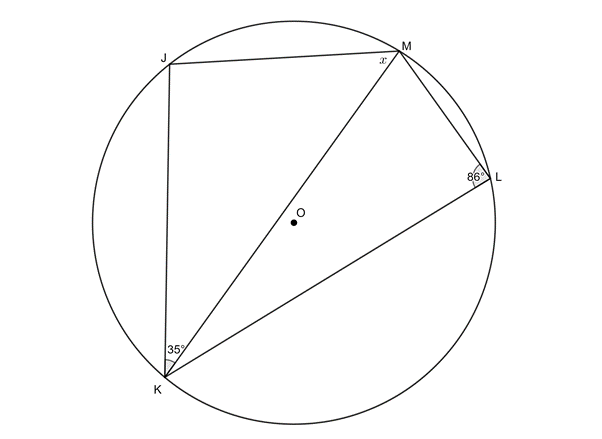
      [latex]\scriptsize \begin{align*}\hat{J}&={{180}^\circ}-{{86}^\circ}\quad \text{(opp }\angle \text{s in cyclic quad)}\\&=9{{\text{4}}^\circ}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}x&={{180}^\circ}-{{94}^\circ}-{{35}^\circ}\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\&=5{{\text{1}}^\circ}\end{align*}[/latex]
   3. .
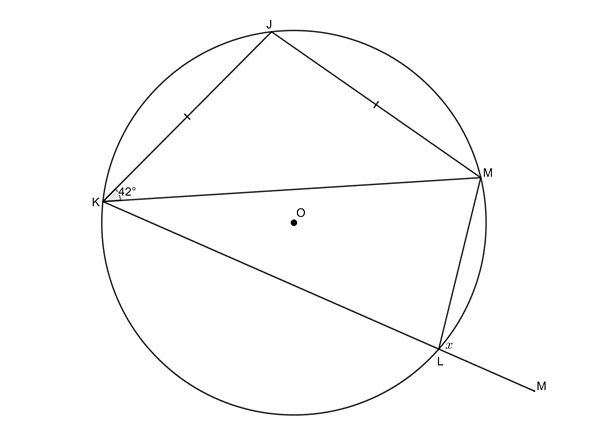
      In [latex]\scriptsize \Delta JKM[/latex]:
      [latex]\scriptsize \begin{align*}K\hat{M}J & ={{42}^\circ}\quad \text{(isosc }\Delta \text{)}\\\therefore K\hat{J}M & ={{180}^\circ}-{{42}^\circ}-{{42}^\circ}\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\ & ={{96}^\circ}\end{align*}[/latex][latex]\scriptsize x=K\hat{J}M={{96}^\circ}\quad \text{(ext }\angle \text{ = opp int }\angle \text{ in cyclic quad)}[/latex]
2. .
   1. .
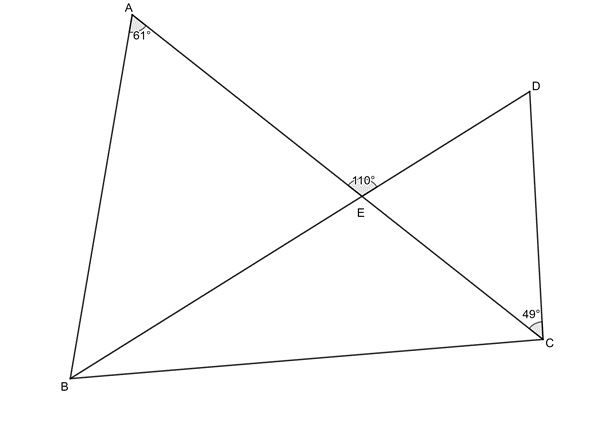
      [latex]\scriptsize \begin{align*}C\hat{E}D&={{180}^\circ}-{{110}^\circ}\quad \text{(}\angle \text{s on a str line)}\\&=\text{7}{{\text{0}}^\circ}\end{align*}[/latex][latex]\scriptsize \begin{align*}B\hat{D}C&={{180}^\circ}-{{70}^\circ}-{{49}^\circ}\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\&=6{{\text{1}}^\circ}\end{align*}[/latex]
      [latex]\scriptsize \therefore B\hat{A}E=C\hat{D}E[/latex]
      Therefore [latex]\scriptsize ABCD[/latex] is a cyclic quadrilateral ([latex]\scriptsize \angle[/latex]s in same segment).
   2. .
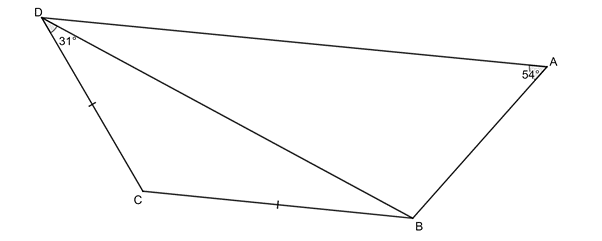
      [latex]\scriptsize \begin{align*}C\hat{B}D & ={{31}^\circ}\quad \text{(isosc }\Delta \text{)}\\\therefore B\hat{C}D & ={{180}^\circ}-{{31}^\circ}-{{31}^\circ}\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\ & ={{118}^\circ}\end{align*}[/latex]
      [latex]\scriptsize B\hat{C}D+B\hat{A}D={{118}^\circ}+{{54}^\circ}={{172}^\circ}[/latex]
      Therefore [latex]\scriptsize ABCD[/latex] is not a cyclic quadrilateral.

Back to Exercise 3.1

Unit 3: Assessment

1. .
   1. .
      [latex]\scriptsize \displaystyle \begin{align*}CB & =DB\quad \text{(given)}\\\therefore B\hat{C}D & =C\hat{D}B\quad \text{(isosc }\Delta \text{)}\\D\hat{P}O & ={{180}^\circ}-{{90}^\circ}={{90}^\circ}\quad \text{(}\angle \text{s on str line suppl)}\\D\hat{P}O & =C\hat{P}O\\\text{In }\Delta \text{ } & CBP\text{:}\\C\hat{B}P & ={{180}^\circ}-C\hat{P}O-B\hat{C}D\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\&=9{{\text{0}}^\circ}-B\hat{C}D\\\text{In }\Delta \text{ } & DBP\text{:}\\D\hat{B}P & ={{180}^\circ}-D\hat{P}O-C\hat{D}B\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\&=9{{\text{0}}^\circ}-C\hat{D}B\\\therefore C\hat{B}P & =D\hat{B}P\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}C\hat{E}D & =C\hat{B}D\quad (\angle \operatorname{s}\text{ in same seg)}\\\text{But }C\hat{B}P & =D\hat{B}P\quad (\text{proven in a}\text{.)}\\\therefore 2\times C\hat{B}A & =C\hat{B}D\\\therefore C\hat{E}D & =2\times C\hat{B}A\end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*}C\hat{O}A & =2\times C\hat{B}A\quad \text{(}\angle \text{ at centre= 2}\angle \text{ at circumference)} & \\\text{But }C\hat{B}P & =D\hat{B}P\quad (\text{proven in a}\text{.)}\\\therefore D\hat{B}P & =\displaystyle \frac{1}{2}C\hat{O}A\end{align*}[/latex]
2. .
   1. [latex]\scriptsize A\hat{C}B=A\hat{B}C={{69}^\circ}\quad \text{(isosc }\Delta \text{)}[/latex]
      [latex]\scriptsize C\hat{D}E=A\hat{B}C={{69}^\circ}\quad \text{(ext }\angle =\text{ opp int }\angle \text{ in cyclic quad)}[/latex]
   2. If [latex]\scriptsize B\hat{A}D={{82}^\circ}[/latex]
      [latex]\scriptsize \begin{align*}B\hat{C}D & ={{180}^\circ}-B\hat{A}D\quad \text{(opp }\angle \text{s in cyclic quad)}\\\therefore B\hat{C}D & ={{180}^\circ}-{{82}^\circ}={{98}^\circ}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}C\hat{D}E & ={{69}^\circ}\quad \text{(proven in a}\text{.)}\\D\hat{C}E & =B\hat{A}D={{82}^\circ}\quad \text{(ext }\angle =\text{ opp int }\angle \text{ in cyclic quad)}\\C\hat{E}D & =180-C\hat{D}E-D\hat{C}E\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\\therefore C\hat{E}D & ={{180}^\circ}-{{69}^\circ}-{{82}^\circ}={{29}^\circ}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}A\hat{C}B & ={{69}^\circ}\quad \text{(proven in a}\text{.)}\\D\hat{C}E & ={{82}^\circ}\quad \text{(proven above)}\\A\hat{C}D & ={{180}^\circ}-A\hat{C}B-D\hat{C}E\quad \text{(}\angle \text{s on a str line suppl)}\\\therefore A\hat{C}D & ={{180}^\circ}-{{69}^\circ}-{{82}^\circ}={{29}^\circ}\\A\hat{B}D & =A\hat{C}D={{29}^\circ}\quad \text{(}\angle \text{s in same seg)}\end{align*}[/latex]

Back to Unit 3: Assessment