Data handling: Use experiments, simulation and probability distribution to set and explore probability models
Unit 1: Understand probability and make predictions
Natashia Bearam-Edmunds
Unit outcomes
By the end of this unit you will be able to:
- Understand the difference between independent and dependent events.
- Understand the difference between mutually inclusive and mutually exclusive events.
- Understand complementary events.
- Identify independent and dependent events using [latex]\scriptsize P~\left( {\text{A }\!\!~\!\!\text{ and }\!\!~\!\!\text{ B}} \right)~=~P~\left( \text{A} \right).P~\left( \text{B} \right)[/latex].
- Use the addition rule for mutually exclusive events [latex]\scriptsize P\left( {\text{A }\!\!~\!\!\text{ or }\!\!~\!\!\text{ B}} \right)=~P\left( \text{A} \right)+~P\left( \text{B} \right)[/latex].
- Use [latex]\scriptsize P(\text{A or B)}=P\text{(A)}+P\text{(B)}-P\text{(A and B)}[/latex] when [latex]\scriptsize P\left( {\text{A}\cap \text{B}} \right)\ne 0[/latex].
What you should know
There is no prior knowledge required for this unit.
Introduction
Probability is often referred to as chance. It is the study of how likely it is that some event will happen.
When your favourite sports team plays a game, you don’t know whether they will win or not. When the weather report says there is a [latex]\scriptsize \displaystyle 40\%[/latex] chance of rain tomorrow, you may or may not end up getting wet. Uncertainty presents itself to some degree in every event that occurs around us and in every decision that we make.
Many events cannot be predicted with absolute certainty. The best we can do is to say how likely they are to happen, using the idea of probability.
Note
You can read about the discovery and history of probability at this link when you have an internet connection.
Experimental and theoretical probability
If we toss a coin [latex]\scriptsize \displaystyle 100[/latex] times, how many times will ‘heads’ come up? We can calculate this using theoretical probability or we can actually perform the experiment, and toss the coin [latex]\scriptsize \displaystyle 100[/latex] times and record the outcomes.
Theoretical probability uses logic and a formula to calculate the chance of an event. An event is one (or more) outcomes. The total number of possible outcomes is called the sample space and is shown using the symbol [latex]\scriptsize \text{S}[/latex]. The number of elements in the sample space is denoted as [latex]\scriptsize n(\text{S})[/latex].
The number of possible outcomes to an event E is denoted [latex]\scriptsize n(\text{E})[/latex].
When we toss a coin there are two possible outcomes, H (heads) or T (tails). Logically we would expect that each outcome has a [latex]\scriptsize \displaystyle 50\%[/latex] chance of happening. We say that there is a theoretical probability of [latex]\scriptsize \displaystyle \frac{1}{2}[/latex] for each outcome. Using theoretical probability, ‘heads’ have half a chance of coming up, so we can expect [latex]\scriptsize \displaystyle 50[/latex] heads in [latex]\scriptsize \displaystyle 100[/latex] coin tosses.
When all possible outcomes of an experiment have an equal chance of occurring, we use the following formula to calculate the theoretical probability:
[latex]\scriptsize \displaystyle \begin{align*}\text{P}(\text{E})&=\text{ }\displaystyle \frac{{\text{number of favourable outcomes}}}{{\text{number of possible outcomes}}}\\&=\displaystyle \frac{{n(\text{E})}}{{n(\text{S})}}\end{align*}[/latex]
Probability values are real numbers between and inclusive of [latex]\scriptsize \displaystyle 0[/latex] and [latex]\scriptsize \displaystyle 1[/latex], measured as a fraction or as a decimal. Probability can also be shown as a percentage between [latex]\scriptsize \displaystyle 0\%[/latex] and [latex]\scriptsize \displaystyle 100\%[/latex]. We use words such as impossible, unlikely, possible, chance, likely and certain when we describe probabilities.
Probabilities can range from impossible to certain. We can see the likelihood of an event on a probability scale.
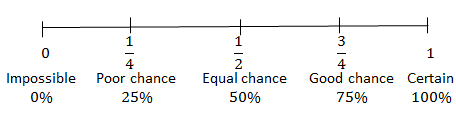
It is impossible, in a test out of [latex]\scriptsize 50[/latex] marks, to get a mark over [latex]\scriptsize 50[/latex].
It is equally likely that a pregnant woman will have a boy or a girl.
It is certain that the sun will rise tomorrow.
We have seen that by using theoretical probability the chance of getting a H when a coin is tossed [latex]\scriptsize \displaystyle 100[/latex] times is [latex]\scriptsize 50[/latex] but when we actually do the experiment we may record [latex]\scriptsize 48[/latex]H or [latex]\scriptsize 55[/latex]H … or anything really, but in most cases it will be a number close to [latex]\scriptsize 50[/latex]. Experimental probability is found from the results of an experiment repeated many times.
The more times the coin is tossed, the more accurate the probability of getting heads becomes and the closer the answer from the experimental probability will be to the theoretical probability.
Example 1.1
Write down the number of possible outcomes (sample space) [latex]\scriptsize n(S)[/latex] for each event below:
- Throwing a .
- Tossing a coin.
- Choosing a card from a pack of playing cards.
Solutions
- When throwing a die, there are [latex]\scriptsize 6[/latex] possible outcomes in total [latex]\scriptsize \displaystyle \left( {1;\text{ }2;\text{ }3;\text{ }4;\text{ }5;\text{ }6} \right)[/latex], so [latex]\scriptsize n(\text{S})=6[/latex].
- A coin has two sides: heads (H) and tails (T), so there are [latex]\scriptsize 2[/latex] possible outcomes [latex]\scriptsize \displaystyle (\text{H; T})[/latex]. Therefore, [latex]\scriptsize n(\text{S})=2[/latex].
- There are [latex]\scriptsize 52[/latex] cards in a pack of cards so there are [latex]\scriptsize 52[/latex] possible outcomes to drawing a card from a pack. A pack of cards has four suits with [latex]\scriptsize 13[/latex] card values in each suit. So there are four cards of each value (i.e. there are [latex]\scriptsize 4[/latex] twos, threes, fours, etc. in a pack). The four suits are diamonds (red), spades (black), hearts (red) and clubs (black). The card values in each suit are [latex]\scriptsize (2;\text{ }3;\text{ }4;\text{ }5;\text{ }6;\text{ }7;\text{ }8;\text{ }9;\text{ }10;\text{ Jack; Queen; King; Ace)}[/latex]. Therefore, [latex]\scriptsize n(\text{S})=52[/latex].
Example 1.2
The letters of the word MATHEMATICS are written on separate cards of the same size. The cards are shuffled and dealt, face down, onto a table. A card is selected at random.
- How many possible outcomes are there?
- What is the probability that the card selected is:
- the letter I?
- the letter M?
- the letter O?
Solutions
- There are [latex]\scriptsize 11[/latex] possible outcomes. [latex]\scriptsize n(S)=11[/latex].
- [latex]\scriptsize \displaystyle \text{Probability}=\text{ }\displaystyle \frac{{\text{number of favourable outcomes}}}{{\text{number of possible outcomes}}}[/latex]
- As there is only one letter ‘I’ there is only one favourable outcome.
[latex]\scriptsize \displaystyle \text{P(I)}=\text{ }\displaystyle \frac{1}{{11}}[/latex] - There are two Ms.
[latex]\scriptsize \displaystyle \text{P(M)}=\text{ }\displaystyle \frac{2}{{11}}[/latex] - There is no letter ‘O’.
[latex]\scriptsize \displaystyle \begin{align*}\text{P(O)}=\text{ }\displaystyle \frac{0}{{11}}\\=0\end{align*}[/latex]
- As there is only one letter ‘I’ there is only one favourable outcome.
Exercise 1.1
- If you roll a die once:
- What is the lowest possible score?
- What is the highest possible score?
- What do you think is the most likely score?
- If you roll a die once, what is the probability of throwing:
- four.
- a prime number.
- an odd number.
- an eight.
- a factor of six.
- a number less than eight.
- A restaurant is having a raffle to raise funds. They sell a total of [latex]\scriptsize \displaystyle 500[/latex] tickets. What is the probability of Andy winning if he bought:
- five tickets?
- [latex]\scriptsize 50[/latex] tickets?
- one ticket?
The full solutions are at the end of the unit.
Dependent and independent events
Using probability, we can work out the chances of two or more events happening.
Events are dependent if the outcome of one event influences the outcome of the other. For example, if your lunchbox contains two apples and one banana, when you eat one of the fruit, this reduces the number of choices you have when deciding to eat a second fruit.
Independent events are not affected by previous events. For example, if you toss a coin and it comes up tails and you toss it again and it lands on heads, neither outcome influences the other. A coin does not ‘know’ it came up heads before, so each toss of the coin is independent.
You can use the product rule for independent events to test if events are independent and to calculate the probability of independent events.
Two events [latex]\scriptsize \text{A}[/latex] and [latex]\scriptsize \text{B}[/latex] are independent if and only if:
[latex]\scriptsize P(\text{A and B)}=P(\text{A})\cdot P(\text{B})[/latex]
Example 1.3
A bag contains five red balls and five blue balls. We remove a ball from the bag at random, record its colour and put it back into the bag. We then remove another ball from the bag and record its colour.
- What is the probability that the first ball is red?
- What is the probability that the second ball is blue?
- What is the probability that the first ball is red and the second ball is blue?
- Are the first ball being red and the second ball being blue independent events?
Solutions
- Since there are a total of [latex]\scriptsize 10[/latex] balls, of which five are red, the probability of getting a red ball is:
[latex]\scriptsize \begin{align*}P(\text{R)}&=\displaystyle \frac{5}{{10}}\\&=\displaystyle \frac{1}{2}\end{align*}[/latex]
Note: always simplify fractions as far as possible when giving the answers to probability questions. - Since the first ball is placed back into the bag before we take the second ball this means that when we draw the second ball, there are still a total of [latex]\scriptsize 10[/latex] balls in the bag, of which five are blue. Therefore the probability of drawing a blue ball is:
[latex]\scriptsize \begin{align*}P(\text{B)}&=\displaystyle \frac{5}{{10}}\\&=\displaystyle \frac{1}{2}\end{align*}[/latex] - When drawing two balls from the bag, there are four possibilities. We can get:
- a red ball and then another red ball
- a red ball and then a blue ball
- a blue ball and then a red ball
- a blue ball and then another blue ball.
.
We want to know the probability of the second outcome, where we have to get a red ball first. Since there are five red balls and [latex]\scriptsize 10[/latex] balls in total, there are [latex]\scriptsize \displaystyle \frac{5}{{10}}[/latex] ways to get a red ball first. Now we put the first ball back, so there are again five red balls and five blue balls in the bag. Therefore, there are [latex]\scriptsize \displaystyle \frac{5}{{10}}[/latex] ways to get a blue ball second if the first ball was red. This means that there are:
[latex]\scriptsize \displaystyle \frac{5}{{10}}\times \displaystyle \frac{5}{{10}}=\displaystyle \frac{{25}}{{100}}[/latex]
ways to get a red ball first and a blue ball second. So, the probability of getting a red ball first and a blue ball second is [latex]\scriptsize \displaystyle \frac{1}{4}[/latex].
- Events are independent if and only if: [latex]\scriptsize P(\text{A and B)}=P(\text{A})\cdot P(\text{B})[/latex]
In this example:- [latex]\scriptsize P(\text{first ball is red)}=\displaystyle \frac{1}{2}[/latex]
- [latex]\scriptsize P(\text{second ball is blue)}=\displaystyle \frac{1}{2}[/latex]
- [latex]\scriptsize P(\text{first ball red and second ball is blue)}=\displaystyle \frac{1}{4}[/latex]
So we see that:
[latex]\scriptsize \begin{align*}P(\text{first ball red and second ball is blue)}&=P(\text{first ball is red)}\cdot P(\text{second ball is blue)}\\&=\displaystyle \frac{1}{2}\cdot \displaystyle \frac{1}{2}\\&=\displaystyle \frac{1}{4}\end{align*}[/latex] Therefore, the events are independent.
In the example above, we picked a random ball and put it back into the bag before continuing. This is called sampling with replacement. In the next example, we will follow the same process, except that we will not put the first ball back into the bag. This is called sampling without replacement.
Example 1.4
A bag contains five red balls and five blue balls. We remove a ball from the bag at random, record its colour. Then, without replacing the first ball, we remove another random ball from the bag and record its colour.
- What is the probability that the first ball is red?
- What is the probability that the second ball is blue?
- What is the probability that the first ball is red and the second ball is blue?
- Are the first ball being red and the second ball being blue independent events?
Solutions
- Since there are five red balls and [latex]\scriptsize 10[/latex] balls in total, there are:
[latex]\scriptsize \displaystyle \frac{5}{{10}}=\displaystyle \frac{1}{2}[/latex] ways to get a red ball first. - There are four possible outcomes when we remove the two balls:
- a red ball and then another red ball
- a red ball and then a blue ball
- a blue ball and then a red ball
- a blue ball and then another blue ball.
.
Since the question asks for the probability that the second ball is blue, we will only consider outcomes two and four. - a red ball and then a blue ball, AND
- a blue ball and then another blue ball.
.
For the first outcome (a red ball and then a blue ball), we get a red ball first. Since there are five red balls and [latex]\scriptsize 10[/latex] balls in total, there are [latex]\scriptsize \displaystyle \frac{5}{{10}}[/latex] ways to get a red ball first.
.
After we have taken out a red ball, there are now four red balls and five blue balls left so that is nine balls altogether. Therefore there are five ways to get a blue ball second if the first ball was red. Therefore, there are [latex]\scriptsize \displaystyle \frac{5}{9}[/latex] ways to get a blue ball second if a red ball was drawn first.
.
This means that there are [latex]\scriptsize \displaystyle \frac{5}{{10}}\times \displaystyle \frac{5}{9}=\displaystyle \frac{{25}}{{90}}[/latex] ways to get a blue ball second if a red ball was drawn first.
.
For the fourth outcome (a blue ball and then another blue ball), we get a blue ball first. Since there are five blue balls and [latex]\scriptsize 10[/latex] balls in total, there are [latex]\scriptsize \displaystyle \frac{5}{{10}}[/latex] ways to get blue ball first.
.
After we have taken out a blue ball, there are now five red balls and four blue balls left so that is nine balls altogether. Therefore there are four ways to get a blue ball second if the first ball was also blue. Therefore, there are [latex]\scriptsize \displaystyle \frac{4}{9}[/latex]ways to get a blue ball second if a blue ball was drawn first.
.
This means that there are [latex]\scriptsize \displaystyle \frac{5}{{10}}\times \displaystyle \frac{4}{9}=\displaystyle \frac{{20}}{{90}}[/latex] ways to get a blue ball second if a blue ball was also drawn first.
.
To determine the probability of getting a blue ball on the second draw, we look at all of the outcomes that contain a blue ball second and add them.
.
[latex]\scriptsize \begin{align*}P(\text{R and B)}+\text{P(B and B)}&=\displaystyle \frac{{25}}{{90}}+\displaystyle \frac{{20}}{{90}}\\&=\displaystyle \frac{{45}}{{90}}\\&=\displaystyle \frac{1}{2}\end{align*}[/latex]
.
This is the same as in the previous example! You might find it surprising that the probability of the second ball being blue is not affected by whether or not we replace the first ball. The reason why this probability is still [latex]\scriptsize \displaystyle \frac{1}{2}[/latex]is that we are computing the probability that the second ball is blue without knowing the colour of the first ball. Because there are only two equal possibilities for the second ball (red and blue) and because we don’t know whether the first ball is red or blue, there is an equal chance that the second ball will be one colour or the other.
- We have already calculated the probability that the first ball is red and the second ball is blue. We saw that there are:
[latex]\scriptsize \begin{align*}\displaystyle \frac{5}{{10}}\times \displaystyle \frac{5}{9}&=\displaystyle \frac{{25}}{{90}}\\&=\displaystyle \frac{5}{{18}}\end{align*}[/latex]
ways to get a blue ball second if a red ball was drawn first. - Events are independent if and only if: [latex]\scriptsize P(\text{A and B)}=P(\text{A})\cdot P(\text{B})[/latex]
In this example:- [latex]\scriptsize P(\text{first ball is red)}=\displaystyle \frac{1}{2}[/latex]
- [latex]\scriptsize P(\text{second ball is blue)}=\displaystyle \frac{1}{2}[/latex]
- [latex]\scriptsize P(\text{first ball red and second ball is blue)}=\displaystyle \frac{5}{{18}}[/latex]
.
So we see that:
.
[latex]\scriptsize \begin{align*}P(\text{first ball red and second ball is blue)}&\ne P(\text{first ball is red)}\cdot P(\text{second ball is blue)}\\\displaystyle \frac{5}{{18}}&\ne \displaystyle \frac{1}{2}\cdot \displaystyle \frac{1}{2}\end{align*}[/latex] Therefore the events are not independent, in other words the events are dependent.
Exercise 1.2
- [latex]\scriptsize P(\text{M})=0.45;\text{ }P(\text{N})=0.35;\text{ }P(\text{M and N})=0.1575[/latex]. Are [latex]\scriptsize \text{M}[/latex] and [latex]\scriptsize \text{N}[/latex] independent events?
- I toss a coin and roll a die. What is the probability of getting a head and a two?
- A box contains three black cards and four white cards. Two cards are randomly picked one after the other.
- Calculate the probability that the first card picked is black.
- Calculate the probability that the first card picked is white.
- If a black card is picked first and not put back into the box, what is the probability that a black card will be picked second?
- If [latex]\scriptsize \text{A}[/latex] and [latex]\scriptsize \text{B}[/latex] are independent events and [latex]\scriptsize P(\text{A})=0.2[/latex] and [latex]\scriptsize P(\text{A and B})=0.06[/latex], find [latex]\scriptsize P(\text{B})[/latex].
The full solutions are at the end of the unit.
Union and intersection
When more than one event occurs at a time there can be a combination of outcomes, which results in unions and intersections of the events.
A union of events is the set of all outcomes that occur in the events, written as:
‘[latex]\scriptsize \displaystyle \text{A}[/latex] or [latex]\scriptsize \displaystyle \text{B}[/latex]’ or [latex]\scriptsize \displaystyle \text{A}\cup \text{B}[/latex] (A union B).
For example, the union of the sets [latex]\scriptsize \text{A}=\{1;\text{ }3;\text{ }5;\text{ }7\}[/latex] and [latex]\scriptsize \text{B}=\{3;\text{ 6};\text{ 9};\text{ 12}\}[/latex] is the new set [latex]\scriptsize \text{A}\cup \text{B}=\{1;\text{ }3;\text{ }5;\text{ }6;\text{ }7;\text{ 9; 12}\}[/latex] which contains all the elements from both sets with no elements repeated. Here [latex]\scriptsize n(A)=4[/latex] and [latex]\scriptsize n(B)=4[/latex], and [latex]\scriptsize n(A\cup B)=7[/latex].
The intersection of events is the set of all outcomes that occur in all of the events. It is written as:
‘[latex]\scriptsize \displaystyle \text{A}[/latex]and [latex]\scriptsize \displaystyle \text{B}[/latex]’ or [latex]\scriptsize \displaystyle \text{A}\cap \text{B}[/latex] (A intersection B).
For example, the intersection of the sets [latex]\scriptsize \text{A}=\{1;\text{ }3;\text{ }5;\text{ }7\}[/latex] and [latex]\scriptsize \text{B}=\{3;\text{ 6};\text{ 9};\text{ 12}\}[/latex] is the new set [latex]\scriptsize \text{A}\cap \text{B}=\{3\}[/latex], which contains all the elements that are common to both the sets. In other words, the intersection contains only the elements repeated in the sets. Here, [latex]\scriptsize n(A\cap B)=1[/latex], meaning that there is only one element that is in both set [latex]\scriptsize \text{A}[/latex] and set [latex]\scriptsize \text{B}[/latex].
We can show the relationships of unions and intersections of sets by using Venn diagrams. We will cover Venn diagrams in detail in unit 2 of this subject outcome.
Note
You can learn more about unions and intersections by watching the video “Venn diagram”.
We can calculate the probability of the union of two events using the addition rule for any two events:
[latex]\scriptsize P(\text{A}\cup \text{B)}=P(\text{A})+P(\text{B})-P(\text{A}\cap \text{B)}[/latex]
Mutually exclusive events
Two events are called mutually exclusive or disjoint if they cannot occur at the same time. For example, you cannot be [latex]\scriptsize 21[/latex]-years-old and [latex]\scriptsize 25[/latex]-years-old at the same time.
Another way of saying this is that the two events, [latex]\scriptsize \displaystyle \text{A}[/latex] and [latex]\scriptsize \displaystyle \text{B}[/latex], cannot have any elements in common, so [latex]\scriptsize n(A\cap B)=0[/latex]. A set with no elements is called ‘the empty set’, and denoted by [latex]\scriptsize \varnothing[/latex]. With no possible events in the sample space, it is clear that [latex]\scriptsize \displaystyle P(\text{A}\cap \text{B)}=0[/latex] .
The addition rule for two mutually exclusive events is [latex]\scriptsize P(\text{A}\cup \text{B)}=P(\text{A})+P(\text{B})[/latex]. This rule is a special case of the previous rule because the events are mutually exclusive, so [latex]\scriptsize \displaystyle P(\text{A}\cap \text{B)}=0[/latex].
Mutually inclusive events are the opposite of mutually exclusive events and can occur at the same time. For example, you could choose a number that is both less than five and odd. There is a possibility of multiple outcomes, so mutually inclusive events cannot happen independently. The probability of the intersection of mutually inclusive events is greater than zero.
[latex]\scriptsize \displaystyle P(\text{A}\cap \text{B)} \gt 0[/latex]
Complementary events
The complement of a set of events [latex]\scriptsize \text{A}[/latex] is a separate set that consists of all elements that are not in [latex]\scriptsize \text{A}[/latex]. The complement of any event is the event not ([latex]\scriptsize \text{A}[/latex]). We write the complement of an event as [latex]\scriptsize \displaystyle A'[/latex]. Since every element in the sample space ([latex]\scriptsize \text{S}[/latex]) is in either [latex]\scriptsize \text{A}[/latex] or [latex]\scriptsize \displaystyle A'[/latex], the union of complementary events covers the entire sample space.
[latex]\scriptsize A\cup A'=S[/latex]
Complementary events occur when there are only two outcomes. For example, passing an exam or not passing an exam.
Since every element in [latex]\scriptsize \text{A}[/latex] is not in [latex]\scriptsize \displaystyle A'[/latex], we know that complementary events are mutually exclusive:
[latex]\scriptsize \displaystyle \text{A}\cap A'=0[/latex]. All complementary events are mutually exclusive, but not all mutually exclusive events are complementary.
The probabilities of complementary events sum to [latex]\scriptsize 1[/latex].
[latex]\scriptsize \begin{array}{l}\text{P}(A)+\text{P}({A}')&=\text{P}(A\cup {A}')\\&=1\\\therefore \text{P}(A)&=1-\text{P}({A}')\end{array}[/latex]
Example 1.5
State if the following are mutually exclusive, mutually inclusive or complementary.
- Day and night.
- Getting a head and getting a tail on a single coin toss.
- Getting a queen and getting a heart in a single draw from a pack of cards.
- Pulling your ear and turning your head.
- Getting a salary increase and not getting a salary increase.
- Rolling a die and getting a five or six.
Solutions
- It cannot be day and night at the same time. These are mutually exclusive and complementary events.
- Getting a head and getting a tail on a single coin toss are mutually exclusive and complementary. You can get either a head or a tail on a single coin toss, but not both at the same time.
- Getting a queen and getting a heart in a single draw from a pack of cards is mutually inclusive. You can get a queen of hearts.
- Pulling your ear and turning your head are mutually inclusive. You can pull your ear and turn your head at the same time.
- Getting a salary increase and not getting a salary increase are mutually exclusive and complementary events.
- Rolling a die and getting a five or six are mutually exclusive events but NOT complementary since there are more than two possible outcomes.
Example 1.6
On a single roll of a die, find the probability of getting:
- one or two .
- A number less than three or a number greater than three.
- An even number.
- An odd number.
- What type of events are those in questions 3 and 4 above called?
Solutions
- The probability of rolling a one or two are mutually exclusive.
[latex]\scriptsize \begin{align*}P(1\text{ or }2)&=P(1)+P(2)\\&=\displaystyle \frac{1}{6}+\displaystyle \frac{1}{6}\\&=\displaystyle \frac{2}{6}\\&=\displaystyle \frac{1}{3}\end{align*}[/latex] - A number less than three or a number greater than three are mutually exclusive. There are two numbers less than three and three numbers greater than three.
[latex]\scriptsize \begin{align*}P(\text{less than }3\cup \text{greater than }3)&=P(\text{less than }3)+P(\text{greater than }3)\\&=\displaystyle \frac{2}{6}+\displaystyle \frac{3}{6}\\&=\displaystyle \frac{5}{6}\end{align*}[/latex] - There are three even numbers.
[latex]\scriptsize \begin{align*}P(\text{even number})&=\displaystyle \frac{3}{6}\\&=\displaystyle \frac{1}{2}\end{align*}[/latex] - There are three odd numbers.
[latex]\scriptsize \begin{align*}P(\text{odd number})&=\displaystyle \frac{3}{6}\\&=\displaystyle \frac{1}{2}\end{align*}[/latex] - Even and odd numbers are complementary events.
Example 1.7
A car dealership has [latex]\scriptsize 200[/latex] cars on its website for sale. If [latex]\scriptsize 50[/latex] of the cars are Toyotas, what is the probability that the next car to be sold is:
- a Toyota?
- not a Toyota?
Solutions
- .
[latex]\scriptsize \begin{align*}P(\text{ }\!\!~\!\!\text{ Toyota})&=\displaystyle \frac{{50}}{{200}}\\&=\displaystyle \frac{1}{4}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}P(\text{ }\!\!~\!\!\text{ Not Toyota})&=1-\displaystyle \frac{1}{4}\\&=\displaystyle \frac{3}{4}\end{align*}[/latex]
Example 1.8
A bowl contains three apples, four lemons and three bananas. If a fruit is selected at random, what is the probability that:
- it is either a lemon or a banana?
- it is not an apple?
- it is a yellow fruit?
Solutions
- These are mutually exclusive events.
[latex]\scriptsize \begin{align*}P(\text{lemon or banana})&=\displaystyle \frac{4}{{10}}+\displaystyle \frac{3}{{10}}\\&=\displaystyle \frac{7}{{10}}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}P(\text{not an apple})&=1-\displaystyle \frac{3}{{10}}\\&=\displaystyle \frac{7}{{10}}\end{align*}[/latex] - Both the lemons and bananas are yellow and these are mutually exclusive.
[latex]\scriptsize \begin{align*}P(\text{yellow fruit)}&=P(\text{banana})+P(\text{lemon})\\&=\displaystyle \frac{7}{{10}}\end{align*}[/latex]
Example 1.9
A card is drawn at random from an ordinary pack of [latex]\scriptsize \displaystyle 52[/latex] playing cards. Find the probability that the card drawn is:
- the three of diamonds
- the three of diamonds or any heart
- a diamond or a three
Solutions
- There is only one three of diamonds in a pack of cards.
[latex]\scriptsize \displaystyle P(3\text{ of diamonds})=\displaystyle \frac{1}{{52}}[/latex] - There are [latex]\scriptsize 13[/latex] hearts in a pack of cards and one three of diamonds. These are mutually exclusive events.
[latex]\scriptsize \displaystyle \begin{align*}P(3\text{ of diamonds or any heart})&=P(3\text{ of diamonds})+P(\text{heart)}\\&=\displaystyle \frac{1}{{52}}+\displaystyle \frac{{13}}{{52}}\\&=\displaystyle \frac{{14}}{{52}}\\&=\displaystyle \frac{7}{{26}}\end{align*}[/latex] - There are four cards of each suit with a value of three. We must subtract the probability of getting a three of diamonds to avoid ‘over counting’.
.
[latex]\scriptsize \displaystyle \begin{align*}P(\text{diamond or 3})&=P(\text{diamond})+P(3\text{)}-P(\text{diamond and 3)}\\&=\displaystyle \frac{{13}}{{52}}+\displaystyle \frac{4}{{52}}-\displaystyle \frac{1}{{52}}\\&=\displaystyle \frac{{16}}{{52}}\\&=\displaystyle \frac{4}{{13}}\end{align*}[/latex]
Exercise 1.3
- A bowl has pink and white sweets. The probability of taking out a pink sweet is [latex]\scriptsize \displaystyle \frac{4}{9}[/latex] . What is the probability of taking out a white sweet?
- You flip a coin two times.
- Write down the sample space.
- What is the probability of getting two heads?
- What is the probability of getting heads first and then tails?
- Donald has [latex]\scriptsize 14[/latex] loose socks in a drawer. Six of these are white and two are red. Calculate the probability that the first sock taken out at random is:
- white
- red
- not red
- white or red
- neither white nor red
- A box contains six orange balls, five green balls and five yellow balls. You randomly pick balls one after the other.
- Calculate the probability of drawing two green balls if the first ball is put back into the box before drawing the second ball.
- Calculate the probability of drawing two green balls if the first ball is NOT put back into the box before drawing the second ball.
- Calculate the probability of drawing a yellow ball and an orange ball if the first ball is put back into the box before drawing the second ball.
- There are [latex]\scriptsize 15[/latex] male (M) and [latex]\scriptsize 20[/latex] female (F) learners in an online lecture. The lecturer randomly chooses a learner to answer a question.
- Determine [latex]\scriptsize P(\text{M})[/latex] learner is chosen.
- Determine [latex]\scriptsize P(\text{F})[/latex].
- If he chooses two learners determine the probability that one is male and the other is female.
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- How to define probability.
- How to calculate theoretical probability.
- How to identify dependent events.
- How to identify independent events.
- How to use the product rule for independent events.
- How to differentiate between mutually exclusive and mutually inclusive events.
- How to use the probability identity [latex]\scriptsize P(\text{A or B)}=P\text{(A)}+P\text{(B)}-P\text{(A and B)}[/latex].
- How to calculate the probability of mutually exclusive events.
- How to calculate the probability of complementary events.
Unit 1: Assessment
Suggested time to complete: 35 minutes
- You take all the hearts from a deck of cards. You then select a random card from the set of hearts.
- What is the sample space?
- Calculate the probability that the card is the ace of hearts.
- Calculate the probability that the card is a prime number.
- Calculate the probability that the card has a letter on it.
- A and B are two events in a sample space where [latex]\scriptsize \displaystyle P(\text{A)}=0.3;\text{ }P(\text{A or B)}=0.8[/latex] and [latex]\scriptsize P(\text{B})=k[/latex]. Determine the value of [latex]\scriptsize k[/latex] if:
- A and B are mutually exclusive.
- A and B are independent.
- You roll two six-sided dice and are interested in the following two events:
A: the sum of the numbers on the dice equals eight
B: at least one of the dice shows a one
Show that these events are mutually exclusive. - The surface of a soccer ball is made up of [latex]\scriptsize \displaystyle 32[/latex] faces. [latex]\scriptsize \displaystyle 12[/latex] faces are regular pentagons, each with a surface area of about [latex]\scriptsize \displaystyle 37\text{ c}{{\text{m}}^{2}}[/latex]. The other [latex]\scriptsize \displaystyle 20[/latex] faces are regular hexagons, each with a surface area of about [latex]\scriptsize \displaystyle \text{56 c}{{\text{m}}^{2}}[/latex]. You roll the soccer ball. What is the probability that it stops with a pentagon touching the ground?
- A pack of [latex]\scriptsize 20[/latex] batteries contains two defective batteries. If two batteries are randomly chosen one after the other, what is the probability that:
- only one of the batteries will be defective?
- both batteries will be defective?
- neither battery will be defective?
- A black bag contains four red beads, nine black beads and seven white beads. You randomly select two beads.
- Calculate the probability of choosing a red bead and then a black bead if the first bead is put back into the bag.
- Calculate the probability of choosing two black beads if the first bead is NOT replaced into the bag.
The full solutions are at the end of the unit.
Unit 1: Solutions
Exercise 1.1
- If you roll a die, the total possible outcomes are [latex]\scriptsize \displaystyle \left( {1;\text{ }2;\text{ }3;\text{ }4;\text{ }5;\text{ }6} \right)[/latex].
- The lowest possible score is one
- The highest possible score is six.
- Are all outcomes just as likely or will some happen more often? All outcomes are equally likely so all have a probability of [latex]\scriptsize \displaystyle \frac{1}{6}[/latex] and no outcome is more likely than another to occur.
- If you roll a die, what is the probability of throwing:
- [latex]\scriptsize \displaystyle P(4)=\displaystyle \frac{1}{6}[/latex]
- There are three prime numbers [latex]\scriptsize (2;\text{ }3;\text{ }5)[/latex].
[latex]\scriptsize \displaystyle \begin{align*}P(\text{prime number})&=\displaystyle \frac{3}{6}\\&=\displaystyle \frac{1}{2}\end{align*}[/latex] - There are three odd numbers [latex]\scriptsize (1;\text{ }3;\text{ }5)[/latex].
[latex]\scriptsize \displaystyle \begin{align*}P(\text{odd number})&=\displaystyle \frac{3}{6}\\&=\displaystyle \frac{1}{2}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}P(8)&=\displaystyle \frac{0}{6}\\&=0\end{align*}[/latex] - There are four factors of [latex]\scriptsize \displaystyle 6[/latex], [latex]\scriptsize (1;\text{ }2;\text{ }3;\text{ }6)[/latex] .
[latex]\scriptsize \displaystyle \begin{align*}P(\text{factor of }6)&=\displaystyle \frac{4}{6}\\&=\displaystyle \frac{2}{3}\end{align*}[/latex] - All the numbers are less than [latex]\scriptsize \displaystyle 8[/latex] so this is a certainty.
[latex]\scriptsize \displaystyle \begin{align*}P(\text{number less than 8})&=\displaystyle \frac{6}{6}\\&=1\end{align*}[/latex]
- .
- .
[latex]\scriptsize \begin{align*}P(\text{winning)}&=\displaystyle \frac{5}{{500}}\\&=1\%\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}P(\text{winning)}&=\displaystyle \frac{{50}}{{500}}\\&=10\%\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}P(\text{winning)}&=\displaystyle \frac{1}{{500}}\\&=0.2\%\end{align*}[/latex]
- .
Exercise 1.2
- [latex]\scriptsize P(\text{M})=0.45;\text{ }P(\text{N})=0.35;\text{ }P(\text{M and N})=0.1575[/latex]
[latex]\scriptsize \begin{align*}P(\text{M})\times P(\text{N})&=0.45\times 0.35\\&=0.1575\end{align*}[/latex]
Since [latex]\scriptsize P(\text{M})\times P(\text{N})=P(\text{M and N})[/latex], [latex]\scriptsize \text{M}[/latex] and [latex]\scriptsize \text{N}[/latex] are independent events. - .
Tossing a coin and rolling a die are independent events.
[latex]\scriptsize P(\text{H)}=\displaystyle \frac{1}{2}[/latex]
[latex]\scriptsize P(\text{2)}=\displaystyle \frac{1}{6}[/latex]
[latex]\scriptsize \begin{align*}P(\text{H and }2)&=\displaystyle \frac{1}{2}\times \displaystyle \frac{1}{6}\\&=\displaystyle \frac{1}{{12}}\end{align*}[/latex] - .
- .
[latex]\scriptsize \begin{align*}P(\text{B)}&=\displaystyle \frac{{\text{number of black cards}}}{{\text{total possible cards}}}\\&=\displaystyle \frac{3}{7}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}P(W\text{)}&=\displaystyle \frac{{\text{number of white cards}}}{{\text{total possible cards}}}\\&=\displaystyle \frac{4}{7}\end{align*}[/latex] - If a black card is picked first and not put back into the box, then there will only be two black cards left in the box and six cards in total.
[latex]\scriptsize \begin{align*}P(\text{B}\text{ first and B second)}&=\displaystyle \frac{3}{7}\times \displaystyle \frac{2}{6}\\&=\displaystyle \frac{6}{{42}}\\&=\displaystyle \frac{1}{7}\end{align*}[/latex]
- .
- Since [latex]\scriptsize \text{A}[/latex] and [latex]\scriptsize \text{B}[/latex] are independent [latex]\scriptsize P(\text{A and B})=P(\text{A})\times P(\text{B})[/latex].
[latex]\scriptsize P(\text{A})=0.2;\text{ }P(\text{A and B})=0.06[/latex]
[latex]\scriptsize \begin{align*}P(\text{A and B})&=P(\text{A})\times P(\text{B})\\0.2\times P(\text{B})&=0.06\\\therefore P(\text{B})&=0.3\end{align*}[/latex]
Exercise 1.3
- .
[latex]\scriptsize \begin{align*}P(\text{W})&=1-P(\text{P})\\&=1-\displaystyle \frac{4}{9}\\&=\displaystyle \frac{5}{9}\end{align*}[/latex] - If you flip a coin two times there are four possible outcomes.
- [latex]\scriptsize \text{S}=\{(\text{H;H), }(\text{H;T), }(\text{T;T), (T;H) }\!\!\}\!\!\text{ }[/latex]
- The probability of getting two heads:
[latex]\scriptsize P(\text{H;H)}=\displaystyle \frac{1}{4}[/latex] - The probability of getting heads first and then tails:
[latex]\scriptsize P(\text{H;T)}=\displaystyle \frac{1}{4}[/latex]
- .
- .
[latex]\scriptsize \begin{align*}P(\text{W)}&=\displaystyle \frac{6}{{14}}\\&=\displaystyle \frac{3}{7}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}P(\text{R)}&=\displaystyle \frac{2}{{14}}\\&=\displaystyle \frac{1}{7}\end{align*}[/latex] - .
[latex]\scriptsize \begin{array}{l}P({R}')&=1-P(R)\\&=1-\displaystyle \frac{1}{7}\\&=\displaystyle \frac{6}{7}\end{array}[/latex] - .
[latex]\scriptsize \begin{align*}P(\text{W}\cup \text{R)}&=P(\text{W)}+P(\text{R)}\\&=\displaystyle \frac{3}{7}+\displaystyle \frac{1}{7}\\&=\displaystyle \frac{4}{7}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}P(\text{neither W nor R})&=1-P(\text{W or R)}\\&=1-\displaystyle \frac{4}{7}\\&=\displaystyle \frac{3}{7}\end{align*}[/latex]
- .
- .
- .
[latex]\scriptsize \begin{align*}P(\text{G and G)}&=\displaystyle \frac{5}{{16}}\cdot \displaystyle \frac{5}{{16}}\\&=\displaystyle \frac{{25}}{{256}}\end{align*}[/latex] - The probability of two green balls if the first ball is not replaced:
[latex]\scriptsize \begin{align*}P(\text{G and G)}&=\displaystyle \frac{5}{{16}}\cdot \displaystyle \frac{4}{{15}}\\&=\displaystyle \frac{1}{{12}}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}P(\text{Y or O)}&=P(\text{Y;O)}+P(\text{O;Y)}\\&=\left( {\displaystyle \frac{5}{{16}}\cdot \displaystyle \frac{6}{{16}}} \right)+\left( {\displaystyle \frac{6}{{16}}\cdot \displaystyle \frac{5}{{16}}} \right)\\&=\displaystyle \frac{{15}}{{64}}\end{align*}[/latex]
- .
- .
- .
[latex]\scriptsize \begin{align*}P(\text{M})&=\displaystyle \frac{{15}}{{35}}\\&=\displaystyle \frac{3}{7}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}P(\text{F})&=\displaystyle \frac{{20}}{{35}}\\&=\displaystyle \frac{4}{7}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}P(\text{M}\cap \text{F})&=P(\text{M})\cdot P(\text{F})\\&=\displaystyle \frac{3}{7}\cdot \displaystyle \frac{4}{7}\\&=\displaystyle \frac{{12}}{{49}}\end{align*}[/latex]
- .
Unit 1: Assessment
- .
- [latex]\scriptsize \text{S}=\{\text{A; 2; 3; 4; 5; 6; 7; 8; 9; 10; J; K; Q}\}[/latex]
- [latex]\scriptsize P(\text{A})=\displaystyle \frac{1}{{13}}[/latex]
- [latex]\scriptsize P(2)+P(3)+P(5)+P(7)=\displaystyle \frac{4}{{13}}[/latex]
- [latex]\scriptsize P(\text{A})+P(\text{J})+P(\text{K})+P(\text{Q})=\displaystyle \frac{4}{{13}}[/latex]
- .
- .
[latex]\scriptsize \displaystyle \begin{align*}P(\text{A or B)}&=0.8\\P(\text{A}\cap \text{B})&=0\text{ since A and B are mutually exclusive}\\P(\text{A or B)}&=P(\text{A})+\text{P(B)}\\0.3+k&=0.8\\\therefore k&=0.5\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}P(\text{A and B)}&=P(\text{A)}\cdot P(\text{B) since A and B are independent}\\&=0.3\times k\\P(\text{A or B)}&=0.8\\P(\text{A)}+P(\text{B)}-P(\text{A and B})&=0.8\\0.3+k-0.3k&=0.8\\0.7k&=0.5\\\therefore k&=\displaystyle \frac{5}{7}\end{align*}[/latex]
- .
- The sum of the dice must equal eight, so it is not possible for one die to show a one, since the other die will have to show a seven, which is not possible.
[latex]\scriptsize n(1\cap 8)=0[/latex] so these events are mutually exclusive. - The total surface area of [latex]\scriptsize \displaystyle 12[/latex] faces of pentagons is [latex]\scriptsize 444\text{ c}{{\text{m}}^{2}}[/latex]. The total surface area of [latex]\scriptsize \displaystyle 20[/latex] hexagons is [latex]\scriptsize 1\text{ }120\text{ c}{{\text{m}}^{2}}[/latex]. The total surface area of the soccer ball is [latex]\scriptsize 1\text{ 564 c}{{\text{m}}^{2}}[/latex].
[latex]\scriptsize \begin{align*}P(\text{pentagon surface})&=\displaystyle \frac{{444}}{{1\text{ }564}}\\&=\displaystyle \frac{{111}}{{391}}\\&=0.28\end{align*}[/latex] - [latex]\scriptsize \text{S}=\{(D;D),\text{ }(D;{D}'),\text{ }({D}';D),\text{ }({D}';{D}')\text{ }\!\!\}\!\!\text{ }[/latex] where [latex]\scriptsize \text{D}[/latex] is defective and [latex]\scriptsize D'[/latex] is not defective.
- .
[latex]\scriptsize \begin{array}{l}P(D\text{ }and\text{ }{D}')=P({{1}^{{st}}}D)\cdot P({{2}^{{nd}}}{D}')+P({{1}^{{st}}}{D}')\cdot P({{2}^{{nd}}}D)\\=\displaystyle \frac{2}{{20}}\cdot \displaystyle \frac{{18}}{{19}}+\displaystyle \frac{{18}}{{20}}\cdot \displaystyle \frac{2}{{19}}\\=\displaystyle \frac{{18}}{{95}}\end{array}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}P(\text{defective and defective)}&=P(\text{defective})\cdot P(\text{defective})\\&=\displaystyle \frac{2}{{20}}\cdot \displaystyle \frac{1}{{19}}\\&=\displaystyle \frac{1}{{190}}\end{align*}[/latex] - .
[latex]\scriptsize \begin{array}{l}P({D}')=1-P(D\text{ and }D)\\=1-\displaystyle \frac{1}{{190}}\\=\displaystyle \frac{{189}}{{190}}\end{array}[/latex]
- .
- .
- .
[latex]\scriptsize \begin{align*}P(\text{R}\text{ and B)}&=\displaystyle \frac{4}{{20}}\cdot \displaystyle \frac{9}{{20}}\\&=\displaystyle \frac{9}{{100}}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}P(\text{B}\text{ and B)}&=\displaystyle \frac{9}{{20}}\cdot \displaystyle \frac{8}{{19}}\\&=\displaystyle \frac{{18}}{{95}}\end{align*}[/latex]
- .
Media Attributions
- Fig 1 Prob scale © DHET is licensed under a CC BY (Attribution) license
the singular of dice; one die and two dice
