Functions and algebra: Investigate and use instantaneous rate of change of a variable when interpreting models both in mathematical and real life situations
Unit 3: Find the equation of a tangent to a curve
Natashia Bearam-Edmunds
Unit outcomes
By the end of this unit you will be able to:
- Define a tangent line.
- Determine the gradient of the tangent at a point.
- Find the equation of a tangent.
What you should know
Before you start this unit, make sure you can:
- Use the rules of differentiation to find the derivative. Revise differentiation rules in unit 2 of this subject outcome and level 3 subject outcome 2.5 unit 3.
Introduction
We have seen that the straight line that touches a curve at one point is a tangent to the curve at that point. In unit 1 we also saw that the gradient at a point on a curve is the same as the gradient of the tangent to the curve at the given point.
Gradients and tangents
If we zoom in on a tangent drawn to a curve, as shown in figure 1, we can see that the tangent touches the curve at a point A.
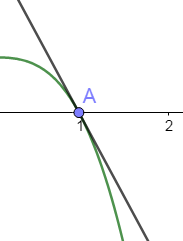
However, further away from point A it is possible for the straight line to cut the curve again, as shown in figure 2.
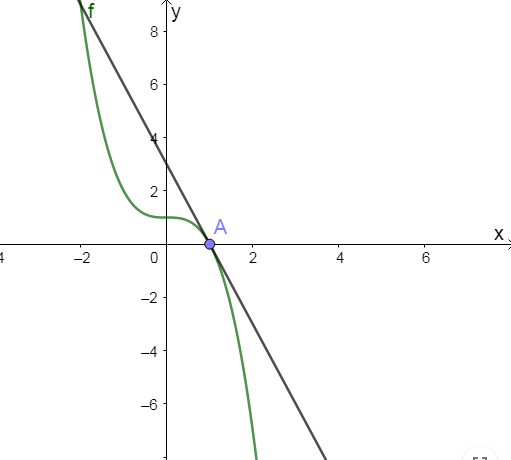
As we can see it is possible for the straight line to be tangential at point A on the curve but intersect the curve again at another point.
Take note!
The tangent to the curve [latex]\scriptsize f(x)[/latex] at the point [latex]\scriptsize \text{A}({{x}_{1}};{{y}_{1}})[/latex] is the straight line through A with gradient [latex]\scriptsize m={f}'({{x}_{1}})[/latex].
Note
For a visual exploration of the tangent line to a curve at a point you can play around with the points found here when you have access to the internet.
Example 3.1
Find the gradient of the tangent to the curve [latex]\scriptsize f(x)=-{{x}^{3}}+1[/latex] at the point [latex]\scriptsize \text{A}(1;0)[/latex].
Solution
The gradient of the tangent at point A is the same as the gradient of the curve at that point.
So, we must find the gradient of [latex]\scriptsize f(x)[/latex] at point A and that will give us the gradient of the tangent to the curve.
To find an expression for the gradient of the curve we find the derivative.
[latex]\scriptsize {f}'(x)=-3{{x}^{2}}[/latex]
Next, substitute the x-value of point A into the derivative and this gives the gradient of the curve at point A.
[latex]\scriptsize \begin{align*}{f}'(1)&=-3{{(1)}^{2}}\\&=-3\end{align*}[/latex]
Therefore, the gradient of the tangent to [latex]\scriptsize f(x)[/latex] at point [latex]\scriptsize \text{A}(1;0)[/latex] is also [latex]\scriptsize -3[/latex].
Example 3.2
Find the point B on the curve [latex]\scriptsize f(x)={{x}^{2}}-4[/latex] at which the gradient of the tangent to the curve is [latex]\scriptsize 6[/latex].
Solution
The gradient of the tangent at point B is the same as the gradient of the curve. Therefore, the gradient of the curve is also [latex]\scriptsize 6[/latex] at point B.
[latex]\scriptsize \begin{align*}{f}'(x)&=6\\\therefore 2x&=6\\x&=3\end{align*}[/latex]
To find the y-value at B:
[latex]\scriptsize \begin{align*}f(3)&={{(3)}^{2}}-4\\&=5\end{align*}[/latex]
Therefore, point B is [latex]\scriptsize (3;5)[/latex].
Exercise 3.1
- Find the gradient of the tangent to the curve [latex]\scriptsize y=-{{x}^{3}}+x-2[/latex] at the point [latex]\scriptsize (1;-2)[/latex].
- Determine the point where the gradient of the tangent to the curve:
- [latex]\scriptsize f(x)=3{{x}^{2}}-2x-1[/latex] is equal to [latex]\scriptsize 3[/latex].
- [latex]\scriptsize y={{x}^{3}}-{{x}^{2}}-5x+2[/latex] is equal to [latex]\scriptsize 0[/latex].
- Determine the point(s) on the curve [latex]\scriptsize f(x)={{(2x-1)}^{2}}[/latex] where the tangent is parallel to the line [latex]\scriptsize y=4x-2[/latex] .
The full solutions are at the end of the unit.
Equation of a tangent to a curve
A tangent line is a straight line, therefore its equation will be of the form [latex]\scriptsize y=mx+c[/latex]. Remember that to find the equation of a straight line, you need its gradient [latex]\scriptsize m[/latex] and the y-intercept [latex]\scriptsize c[/latex].
To determine the equation of a tangent to a curve:
- Find the derivative using the rules of differentiation.
- Substitute the x-coordinate of the given point into the derivative to calculate the gradient of the tangent.
- Substitute the gradient of the tangent and the coordinates of the given point into an appropriate form of the straight line equation.
- Make [latex]\scriptsize y[/latex] the subject of the formula to write the equation in standard form.
Example 3.3
Find the equation of the tangent to the curve [latex]\scriptsize f(x)=-{{x}^{3}}+1[/latex] at the point [latex]\scriptsize \text{A}(1;0)[/latex].
Solution
Step 1: Find the derivative.
[latex]\scriptsize {f}'(x)=-3{{x}^{2}}[/latex]
Step 2: Find the gradient of the tangent.
Substitute the x-coordinate of the given point into the derivative to calculate the gradient of the tangent.
[latex]\scriptsize \begin{align*}{f}'(1)&=-3{{(1)}^{2}}\\&=-3\end{align*}[/latex]
Step 3: Determine the equation of the tangent.
Substitute the gradient of the tangent and the coordinates of the given point into an appropriate form of the straight line equation.
[latex]\scriptsize y=mx+c[/latex]
[latex]\scriptsize m=-3[/latex]
Find the y-intercept [latex]\scriptsize c[/latex] by substituting [latex]\scriptsize \text{A}(1;0)[/latex].
[latex]\scriptsize \begin{align*}y&=-3x+c\\0&=-3(1)+c\\\therefore c&=3\end{align*}[/latex]
Step 4: Write the equation in standard form.
Make y the subject of the formula.
[latex]\scriptsize y=-3x+3[/latex]
Example 3.4
Given [latex]\scriptsize g(x)=(x+2){{(2x+1)}^{2}}[/latex], determine the equation of the tangent to the curve at [latex]\scriptsize x=-1[/latex].
Solution
Step 1: Determine the y-coordinate of the point.
[latex]\scriptsize \begin{align*}g(-1)&=(-1+2){{(2(-1)+1)}^{2}}\\&=1\end{align*}[/latex]
Therefore, the tangent to the curve passes through the point [latex]\scriptsize (-1;1)[/latex].
Step 2: Expand and simplify the given function.
[latex]\scriptsize \begin{align*}g(x)&=(x+2){{(2x+1)}^{2}}\\&=(x+2)(4{{x}^{2}}+4x+1)\\&=4{{x}^{3}}+4{{x}^{2}}+x+8{{x}^{2}}+8x+2\\&=4{{x}^{3}}+12{{x}^{2}}+9x+2\end{align*}[/latex]
Step 3: Find the derivative.
[latex]\scriptsize {g}'(x)=12{{x}^{2}}+24x+9[/latex]
Step 4: Calculate the gradient of the tangent.
[latex]\scriptsize \begin{align*}{g}'(x)&=12{{(-1)}^{2}}+24(-1)+9\\&=-3\\\therefore m&=-3\end{align*}[/latex]
Step 5: Determine the equation of the tangent.
You can substitute the gradient of the tangent and the coordinates of the point into the gradient point form of the straight line equation.
[latex]\scriptsize \begin{align*}y-{{y}_{1}}&=m(x-{{x}_{1}})\\y-1&=-3(x-(-1))\\y&=-3x-3+1\\y&=-3x-2\end{align*}[/latex]
Exercise 3.2
- Find the equation of the tangent to the curve [latex]\scriptsize xy=9[/latex] at [latex]\scriptsize (3;3)[/latex].
- Given the function [latex]\scriptsize f(x)=-{{x}^{2}}+4x-3[/latex], find the equation of the tangent at:
- the y-intercept of [latex]\scriptsize f[/latex].
- the turning point of [latex]\scriptsize f[/latex].
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- How to find the gradient of a tangent to a curve at a point.
- How to find the point where the tangent touches the curve.
- How to find the equation of the tangent to a curve.
Unit 3: Assessment
Suggested time to complete: 20 minutes
- Determine the point where the tangent to the curve [latex]\scriptsize g(x)={{x}^{2}}-4x-5[/latex]:
- is parallel to the line [latex]\scriptsize y=2x-1[/latex].
- is perpendicular to the line [latex]\scriptsize y=2x-1[/latex].
- Find the equation of the tangent to the curve [latex]\scriptsize f(x)={{x}^{3}}+2{{x}^{2}}+7x+1[/latex] at [latex]\scriptsize x=2[/latex].
- Find the equation of the line perpendicular to the tangent to the curve [latex]\scriptsize f(x)=2{{x}^{2}}-x+3[/latex] at the point [latex]\scriptsize (2;9)[/latex].
The full solutions are at the end of the unit.
Unit 3: Solutions
Exercise 3.1
- .
[latex]\scriptsize {y}'=-3{{x}^{2}}+1[/latex] is the gradient of the tangent to the curve at any point.
To find the gradient of the tangent at [latex]\scriptsize (1;-2)[/latex] substitute the x-value into the gradient equation.
[latex]\scriptsize \begin{align*}{y}'(1)&=-3{{(1)}^{2}}+1\\&=-2\end{align*}[/latex] - .
- .
[latex]\scriptsize \begin{align*}{f}'(x)&=6x-2\\{f}'(x)&=3\\\therefore 6x-2&=3\\x&=\displaystyle \frac{5}{6}\end{align*}[/latex]
[latex]\scriptsize \text{Substitute back into }f(x)\text{ to find the y-value}[/latex]
[latex]\scriptsize \begin{align*}f\left( {\displaystyle \frac{5}{6}} \right)&=3{{\left( {\displaystyle \frac{5}{6}} \right)}^{2}}-2\left( {\displaystyle \frac{5}{6}} \right)-1\\&=\displaystyle \frac{{-7}}{{12}}\end{align*}[/latex]
The point at which the gradient is [latex]\scriptsize 3[/latex] is [latex]\scriptsize \left( {\displaystyle \frac{5}{6};-\displaystyle \frac{7}{{12}}} \right)[/latex]. - .
[latex]\scriptsize \displaystyle \begin{align*}{y}' &=3{{x}^{2}}-2x-5\\3{{x}^{2}}-2x-5&=0\\(3x-5)(x+1)&=0\\x&=\displaystyle \frac{5}{3}\text{ or }x=-1\end{align*}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}f\left( {\displaystyle \frac{5}{3}} \right)&={{\left( {\displaystyle \frac{5}{3}} \right)}^{3}}-{{\left( {\displaystyle \frac{5}{3}} \right)}^{2}}-5\left( {\displaystyle \frac{5}{3}} \right)+2\\&=\displaystyle \frac{{-121}}{{27}}\\f(-1)&={{(-1)}^{3}}-{{(-1)}^{2}}-5(-1)+2\\&=5\end{align*}[/latex]
The gradient of the tangent is equal to [latex]\scriptsize 0[/latex] at [latex]\scriptsize (\displaystyle \frac{5}{3};-\displaystyle \frac{{121}}{{27}})[/latex] and [latex]\scriptsize (-1;5)[/latex].
- .
- .
Parallel lines have equal gradients.
Therefore, the gradient of the tangent is [latex]\scriptsize 4[/latex].
[latex]\scriptsize \begin{align*}f(x)&=4{{x}^{2}}-4x+1\\{f}'(x)&=8x-4\\8x-4&=4\\x&=1\\f(1)&=4{{(1)}^{2}}-4(1)+1\\&=1\end{align*}[/latex]
The gradient of the tangent is equal to [latex]\scriptsize 4[/latex] at [latex]\scriptsize (1;1)[/latex].
Exercise 3.2
- .
[latex]\scriptsize \begin{align*}y&=\displaystyle \frac{9}{x}\\&=9{{x}^{{-1}}}\\{y}' &=-9{{x}^{{-2}}}\\&=\displaystyle \frac{{-9}}{{{{x}^{2}}}}\\{y}'(3)&=\displaystyle \frac{{-9}}{{{{{(3)}}^{2}}}}\\&=-1\end{align*}[/latex]
Equation of the tangent:
[latex]\scriptsize \begin{align*}y-3&=-1(x-3)\\y&=-x+6\end{align*}[/latex] - .
- the y-intercept of [latex]\scriptsize f[/latex] is [latex]\scriptsize (0;-3)[/latex]
[latex]\scriptsize \begin{align*}{f}'(x)&=-2x+4\\{f}'(-3)&=-2(-3)+4\\&=10\end{align*}[/latex]
Equation of the tangent:
[latex]\scriptsize \begin{align*}y-(-3)&=10(x-0)\\y&=10x-3\end{align*}[/latex] - the turning point of [latex]\scriptsize f[/latex]:
[latex]\scriptsize \begin{align*}{f}'(x)&=-2x+4=0\\x&=2\\f(2)&=-{{(2)}^{2}}+4(2)-3\\&=1\end{align*}[/latex]
The gradient of the tangent at the turning point is zero:
[latex]\scriptsize \begin{align*}{f}'(2)&=-2(2)+4\\&=0\end{align*}[/latex]
The equation of the tangent:
[latex]\scriptsize \begin{align*}y-1&=0(x-2)\\y&=1\end{align*}[/latex]
- the y-intercept of [latex]\scriptsize f[/latex] is [latex]\scriptsize (0;-3)[/latex]
Unit 3: Assessment
- .
- Gradients of parallel lines are equal.
[latex]\scriptsize \begin{align*}{g}'(x)&=2\\2x-4&=2\\x&=3\end{align*}[/latex]
Find the y-value.
[latex]\scriptsize \begin{align*}g(3)&={{(3)}^{2}}-4(3)-5\\&=-8\end{align*}[/latex]
There is a tangent at the point [latex]\scriptsize (3;8)[/latex]. - The product of the gradients of perpendicular lines is equal to [latex]\scriptsize -1[/latex].
[latex]\scriptsize {{m}_{1}}\times {{m}_{2}}=-1[/latex]
Therefore, the gradient of the tangent is [latex]\scriptsize -\displaystyle \frac{1}{2}[/latex] since [latex]\scriptsize -\displaystyle \frac{1}{2}\times 2=-1[/latex].
[latex]\scriptsize \begin{align*}{g}'(x)&=\displaystyle \frac{{-1}}{2}\\2x-4&=\displaystyle \frac{{-1}}{2}\\x&=\displaystyle \frac{7}{4}\end{align*}[/latex]
Find the y-value.
[latex]\scriptsize \begin{align*}g\left( {\displaystyle \frac{7}{4}} \right)&={{\left( {\displaystyle \frac{7}{4}} \right)}^{2}}-4\left( {\displaystyle \frac{7}{4}} \right)-5\\&=\displaystyle \frac{{-143}}{{16}}\end{align*}[/latex]
There is a tangent at the point [latex]\scriptsize (\displaystyle \frac{7}{4};\displaystyle \frac{{-143}}{{16}})[/latex] .
- Gradients of parallel lines are equal.
- Find the equation of the tangent to the curve [latex]\scriptsize f(x)={{x}^{3}}+2{{x}^{2}}+7x+1[/latex] at [latex]\scriptsize x=2[/latex].
[latex]\scriptsize \begin{align*}f(2)&={{(2)}^{3}}+2{{(2)}^{2}}+7(2)+1\\&=31\end{align*}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}{f}'(x)&=3{{x}^{2}}+4x+7\\{f}'(2)&=3{{(2)}^{2}}+4(2)+7\\&=27\end{align*}[/latex]
Equation of the tangent:
[latex]\scriptsize \begin{align*}y-31&=27(x-2)\\y&=27x-54+31\\y&=27x-23\end{align*}[/latex] - The product of the gradients of perpendicular lines equals [latex]\scriptsize -1[/latex]. So, the gradient of the tangent will be the negative reciprocal of the perpendicular line.
[latex]\scriptsize \begin{align*}{f}'(x)&=4x-1\\{f}'(2)&=4(2)-1\\&=7\end{align*}[/latex]
Gradient of perpendicular line is [latex]\scriptsize -\displaystyle \frac{1}{7}[/latex]. Use the point [latex]\scriptsize (2;9)[/latex]to find the equation.
[latex]\scriptsize \begin{align*}y-9&=-\displaystyle \frac{1}{7}(x-2)\\y&=-\displaystyle \frac{1}{7}x+\displaystyle \frac{{65}}{7}\end{align*}[/latex]
Media Attributions
- Fig 1 Tangent to a curve © DHET is licensed under a CC BY (Attribution) license
- Fig 2 Tangent zoomed out © DHET is licensed under a CC BY (Attribution) license
