Data handling: Use variance and regression analysis to interpolate and extrapolate bivariate data

Unit 3: Linear regression analysis

Gill Scott

Unit outcomes

By the end of this unit you will be able to:

  • Determine the linear regression equation [latex]\scriptsize \hat{y}=a+bx[/latex].
  • Use the regression line to predict the outcome of a given problem.

What you should know

Before you start this unit, make sure you can:

Introduction

Unit 2 of this subject outcome focused on drawing scatter plots of given bivariate data sets, and intuitively drawing lines of best fit between the two components of the plotted points. The obvious next step in this process is to use a more reliable system than intuition to find the lines of best fit. This unit explains the ‘least squares regression’ method of determining a straight-line function that best fits a given set of bivariate data.

Residuals

In example 2.1 from unit 2 of this subject outcome we drew an intuitive line of best fit of data measuring the number of sweets children ate per week against their average number of hours’ sleep per day. The data and the scatter plot with best fit line are repeated below:

No. sweets per week [latex]\scriptsize 15[/latex] [latex]\scriptsize 9[/latex] [latex]\scriptsize 10[/latex] [latex]\scriptsize 6[/latex] [latex]\scriptsize 23[/latex] [latex]\scriptsize 8[/latex] [latex]\scriptsize 13[/latex] [latex]\scriptsize 3[/latex]
Average hours’ sleep per day [latex]\scriptsize 4.5[/latex] [latex]\scriptsize 5[/latex] [latex]\scriptsize 6[/latex] [latex]\scriptsize 7[/latex] [latex]\scriptsize 3[/latex] [latex]\scriptsize 5[/latex] [latex]\scriptsize 4[/latex] [latex]\scriptsize 8.5[/latex]
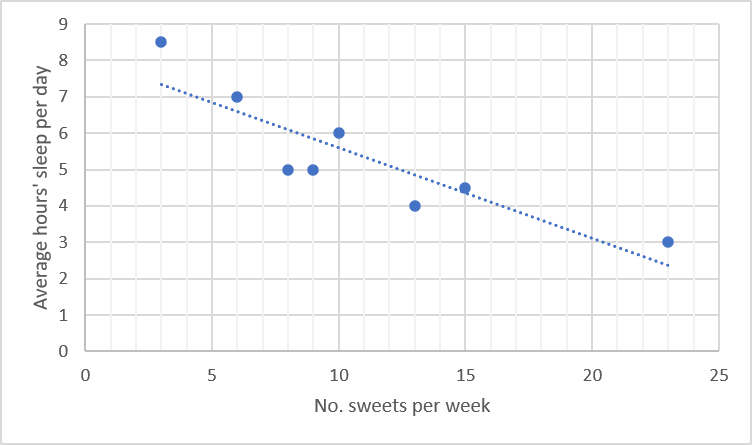
Figure 1: Scatter plot and best fit line from example 2.1 from unit 2 of this subject outcome

In this example, we intuitively found the line of best fit and we saw that the equation of the line would be different for different people, depending on which coordinates we chose to use. For mathematical accuracy and consistency, we need a method that will give one single equation of the line of best fit for a given dataset. This method is called linear regression.

The form of the linear regression equation preferred by statisticians for the best fit straight line, is [latex]\scriptsize \hat{y}=a+bx[/latex]. We say ‘y hat’: statistics uses the ‘hat’ operator ‘ˆ’ to indicate that a value is an estimation. The intercept on the y-axis is [latex]\scriptsize a[/latex], and [latex]\scriptsize b[/latex] is the slope of the line. This equation is a variant of the familiar [latex]\scriptsize y=mx+c[/latex] straight-line equation, with [latex]\scriptsize \displaystyle a[/latex] instead of [latex]\scriptsize \displaystyle c[/latex], and [latex]\scriptsize \displaystyle b[/latex] instead of [latex]\scriptsize m[/latex].

Where [latex]\scriptsize x[/latex] is the independent variable, the best-fit straight line is the one where the sum of the deviations of y-distances from each given point to the line is a minimum. This distance, [latex]\scriptsize y-\hat{y}[/latex], is called the residual. The strategy of squaring, as used in calculating standard deviation, solves the problem of negative residuals cancelling out those that are positive.

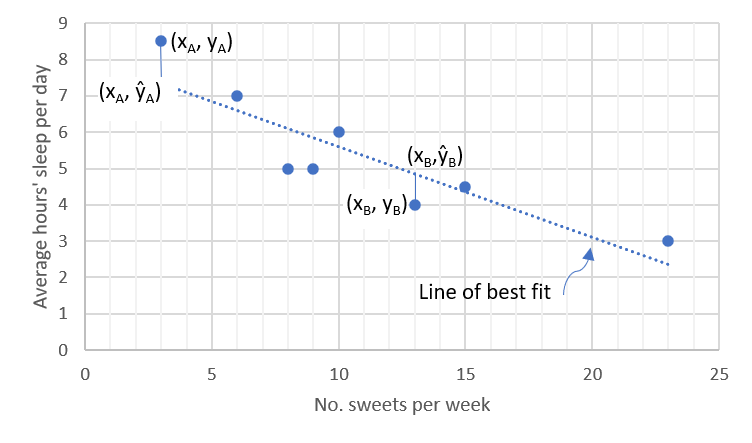
Figure 2: Scatter plot with estimated line of best fit from example 2.1 from unit 2 of this subject outcome

Activity 3.1: Calculating the distances from data points to ŷ, the line of best fit

Time required: 20 minutes

What you need:

  • a pen
  • paper (preferably graph paper)
  • a ruler

What to do:

  1. With [latex]\scriptsize \hat{y}[/latex] being the line of best fit (the dotted line in the graph above):
    1. Read off the [latex]\scriptsize \hat{y}[/latex] coordinate for each [latex]\scriptsize x[/latex] value plotted from the given data set. Note it down in a copy of the table below.
    2. Measure as accurately as you can the vertical distance from each plotted data point to the best fit line. Note this in the [latex]\scriptsize y-\hat{y}[/latex] column with the appropriate sign, whether positive or negative.
  2. Calculate the ‘residual’ [latex]\scriptsize y-\hat{y}[/latex] for each [latex]\scriptsize x[/latex] value, noting it in the table.
  3. Calculate the squared error for each given data point and the best fit straight line. Note these in the appropriate column.
  4. Calculate the sum of the residuals and note it in the table.
  5. Write down what the sum of residuals says about how well [latex]\scriptsize \hat{y}[/latex] fits to the data.
  6. Calculate the sum of the squared error values, and note this in the table.
  7. Discuss what the value of the squared error says about the goodness of fit of [latex]\scriptsize \hat{y}[/latex] to the data.
    No. sweets per week

    [latex]\scriptsize x[/latex]

    		 Average hours’ sleep per night

    [latex]\scriptsize y[/latex]

    		 [latex]\scriptsize \hat{y}[/latex] Residual

    [latex]\scriptsize y- \hat{y}[/latex]

    		 Squared error

    [latex]\scriptsize (y- \hat{y})^2[/latex]
    [latex]\scriptsize 15[/latex] [latex]\scriptsize 4.5[/latex]
    [latex]\scriptsize 9[/latex] [latex]\scriptsize 5[/latex]
    [latex]\scriptsize 10[/latex] [latex]\scriptsize 6[/latex]
    [latex]\scriptsize 6[/latex] [latex]\scriptsize 7[/latex]
    [latex]\scriptsize 23[/latex] [latex]\scriptsize 3[/latex]
    [latex]\scriptsize 8[/latex] [latex]\scriptsize 5[/latex]
    [latex]\scriptsize 13[/latex] [latex]\scriptsize 4[/latex]
    [latex]\scriptsize 3[/latex] [latex]\scriptsize 8.5[/latex]
    Sums

What did you find?

Your [latex]\scriptsize \hat{y}[/latex] values may differ slightly from those inserted in the table below. You will probably find that it is difficult to be completely accurate.

Answers to questions 1. to 4. and 6. are in the table below.

No. sweets per week

[latex]\scriptsize x[/latex]

 Average hours’ sleep per night

[latex]\scriptsize y[/latex]

 [latex]\scriptsize \hat{y}[/latex] Residual

[latex]\scriptsize y- \hat{y}[/latex]

 Squared error

[latex]\scriptsize (y- \hat{y})^2[/latex]
[latex]\scriptsize 15[/latex] [latex]\scriptsize 4.5[/latex] [latex]\scriptsize 4.4[/latex] [latex]\scriptsize 0.1[/latex] [latex]\scriptsize 0.01[/latex]
[latex]\scriptsize 9[/latex] [latex]\scriptsize 5[/latex] [latex]\scriptsize 5.8[/latex] [latex]\scriptsize -0.8[/latex] [latex]\scriptsize 0.64[/latex]
[latex]\scriptsize 10[/latex] [latex]\scriptsize 6[/latex] [latex]\scriptsize 5.6[/latex] [latex]\scriptsize 0.4[/latex] [latex]\scriptsize 0.16[/latex]
[latex]\scriptsize 6[/latex] [latex]\scriptsize 7[/latex] [latex]\scriptsize 6.7[/latex] [latex]\scriptsize 0.3[/latex] [latex]\scriptsize 0.09[/latex]
[latex]\scriptsize 23[/latex] [latex]\scriptsize 3[/latex] [latex]\scriptsize 2.3[/latex] [latex]\scriptsize 0.7[/latex] [latex]\scriptsize 0.49[/latex]
[latex]\scriptsize 8[/latex] [latex]\scriptsize 5[/latex] [latex]\scriptsize 6.1[/latex] [latex]\scriptsize -1.1[/latex] [latex]\scriptsize 1.21[/latex]
[latex]\scriptsize 13[/latex] [latex]\scriptsize 4[/latex] [latex]\scriptsize 4.9[/latex] [latex]\scriptsize -0.9[/latex] [latex]\scriptsize 0.81[/latex]
[latex]\scriptsize 3[/latex] [latex]\scriptsize 8.5[/latex] [latex]\scriptsize 7.4[/latex] [latex]\scriptsize 1.1[/latex] [latex]\scriptsize 1.21[/latex]
Sums [latex]\scriptsize -0.2[/latex] [latex]\scriptsize 4.62[/latex]
  1. The sum of residuals is not a good indicator of how well [latex]\scriptsize \hat{y}[/latex] fits to the data. Although the [latex]\scriptsize -0.2[/latex] sum is quite a small value, this could easily be the result of large positive and negative differences cancelling each other out.
  2. The sum of squared error does relate to how well [latex]\scriptsize \hat{y}[/latex] fits to the data: the smaller this sum, the closer the line is to each of the data points. However, this value in itself does not seem to be helpful in the actual plotting of the line of best fit.

Finding the equation [latex]\scriptsize \hat{y}=a+bx[/latex] of a straight line of best fit

The formula for finding the gradient of the line of best fit of a set of bivariate data points uses the mean and standard deviation of all the [latex]\scriptsize x \text{-values}[/latex], and the mean and standard deviation of the given [latex]\scriptsize y \text{-values}[/latex] .

Take note!

The derivation of the formulae used for finding the equation of the line is fairly complicated and is not required at this level.

Note

If you would like to investigate the derivation of the formulae, when you have access to the internet, watch the series of videos starting at “Introduction to residuals and least squares regression”.

Introduction to residuals and least squares regression (Duration: 07.39)

Multiplying binomials

You can also read “Introduction to residuals” by Khan Academy.

Introduction to residuals

The equation [latex]\scriptsize \hat{y}=a+bx[/latex] of the straight line of best fit satisfies the following conditions:

  • The formulae are based on the fact that [latex]\scriptsize x[/latex] is the independent variable, and [latex]\scriptsize y[/latex] is the dependent variable (this is an important requirement).
  • The point [latex]\scriptsize (\bar{x},\text{ }\bar{y})[/latex] lies on the line of best fit, where [latex]\scriptsize \bar{x}[/latex] is the mean of all the given [latex]\scriptsize x\text{-values}[/latex] in the dataset, and [latex]\scriptsize \bar{y}[/latex] is the mean of all the given [latex]\scriptsize y\text{-values}[/latex].
  • The gradient: [latex]\scriptsize b=\displaystyle \frac{{\sum{{(x-\bar{x})(y-\bar{y})}}}}{{\sum{{{{{(x-\bar{x})}}^{2}}}}}}[/latex]
    You will remember that the standard deviation also used the difference between data values and their means.
  • The y-intercept: [latex]\scriptsize a=\displaystyle \frac{{\sum{{y-b\sum{x}}}}}{n}=\bar{y}-b\bar{x}[/latex] where [latex]\scriptsize b[/latex] is the gradient of the best-fit line.
  • The sum of residuals is [latex]\scriptsize 0[/latex].
  • The mean of residuals is [latex]\scriptsize 0[/latex].
  • The sum of squares of residuals is a minimum.

The first bullet point above is a requirement, and the next three bullets are the tools we use to find the equation of the line of best fit.

Example 3.1

This example further develops question 2 from exercise 2.1 of unit 2 in this subject outcome.
Example adapted from Siyavula Grade 12 Mathematics Exercise 9-2

Dr Dandara is a scientist trying to find a cure for a disease which has an [latex]\scriptsize 80\%[/latex] mortality rate. That means that [latex]\scriptsize 80\%[/latex] of people who get the disease will die. He knows of a plant which is used in traditional medicine to treat the disease. He extracts the active ingredient from the plant and tests different dosages (measured in milligrams) on different groups of patients. Examine the data below and complete the questions that follow.

Dosage (mg) [latex]\scriptsize 0[/latex] [latex]\scriptsize 25[/latex] [latex]\scriptsize 50[/latex] [latex]\scriptsize 75[/latex] [latex]\scriptsize 100[/latex] [latex]\scriptsize 125[/latex] [latex]\scriptsize 150[/latex] [latex]\scriptsize 175[/latex] [latex]\scriptsize 200[/latex]
Mortality rate ([latex]\scriptsize \%[/latex]) [latex]\scriptsize 80[/latex] [latex]\scriptsize 73[/latex] [latex]\scriptsize 63[/latex] [latex]\scriptsize 49[/latex] [latex]\scriptsize 42[/latex] [latex]\scriptsize 32[/latex] [latex]\scriptsize 25[/latex] [latex]\scriptsize 11[/latex] [latex]\scriptsize 5[/latex]
  1. Draw the scatter plot of the data on graph paper.
  2. Use the formulae for [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] to find the regression equation for the line of best fit.
  3. Draw the line of best fit on the scatter plot. Compare this line to the best fit line you drew in unit 2.
  4. Use the equation of the line of best fit to estimate the dosage required for a [latex]\scriptsize 0\%[/latex] mortality rate.

Solution

  1. .
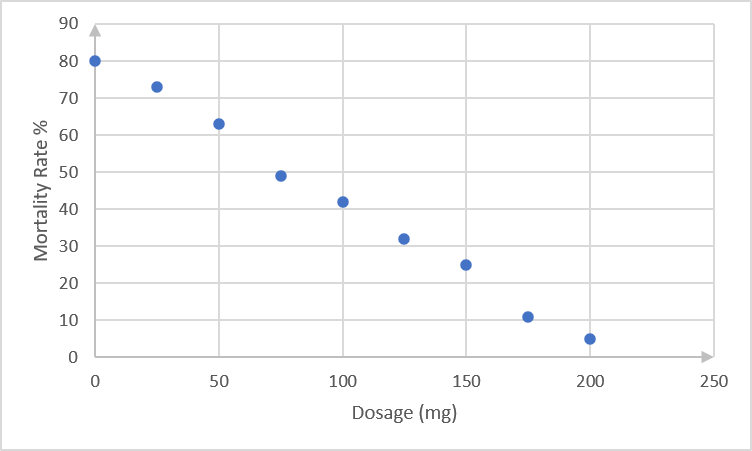
  2. It is best to tabulate the data in these questions to be able to check your answers. Also, the Assessment Guidelines require that these values should be calculated ‘manually’ – that is without using your calculator’s statistical function. Examination questions also sometimes stipulate that calculator statistical functions should not be used. For this reason, this approach has been adopted in this unit.
    Dosage (mg)

    [latex]\scriptsize x[/latex]

    		 Mortality rate ([latex]\scriptsize \%[/latex])

    [latex]\scriptsize y[/latex]

    		 [latex]\scriptsize x-\bar{x}[/latex] [latex]\scriptsize y-\bar{y}[/latex] [latex]\scriptsize (x-\bar{x})(y-\bar{y})[/latex] [latex]\scriptsize (x-\bar{x})^2[/latex]
    [latex]\scriptsize 0[/latex] [latex]\scriptsize 80[/latex] [latex]\scriptsize -100[/latex] [latex]\scriptsize 37.8[/latex] [latex]\scriptsize -3~777.8[/latex] [latex]\scriptsize 10~000[/latex]
    [latex]\scriptsize 25[/latex] [latex]\scriptsize 73[/latex] [latex]\scriptsize -75[/latex] [latex]\scriptsize 30.8[/latex] [latex]\scriptsize -2~308.3[/latex] [latex]\scriptsize 5~625[/latex]
    [latex]\scriptsize 50[/latex] [latex]\scriptsize 63[/latex] [latex]\scriptsize -50[/latex] [latex]\scriptsize 20.8[/latex] [latex]\scriptsize -1~038.9[/latex] [latex]\scriptsize 2~500[/latex]
    [latex]\scriptsize 75[/latex] [latex]\scriptsize 49[/latex] [latex]\scriptsize -25[/latex] [latex]\scriptsize 6.8[/latex] [latex]\scriptsize -169.4[/latex] [latex]\scriptsize 625[/latex]
    [latex]\scriptsize 100[/latex] [latex]\scriptsize 42[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -0.2[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize 0[/latex]
    [latex]\scriptsize 125[/latex] [latex]\scriptsize 32[/latex] [latex]\scriptsize 25[/latex] [latex]\scriptsize -10.2[/latex] [latex]\scriptsize -255.6[/latex] [latex]\scriptsize 626[/latex]
    [latex]\scriptsize 150[/latex] [latex]\scriptsize 25[/latex] [latex]\scriptsize 50[/latex] [latex]\scriptsize -17.2[/latex] [latex]\scriptsize -861.1[/latex] [latex]\scriptsize 2~500[/latex]
    [latex]\scriptsize 175[/latex] [latex]\scriptsize 11[/latex] [latex]\scriptsize 75[/latex] [latex]\scriptsize -31.2[/latex] [latex]\scriptsize -2~341.7[/latex] [latex]\scriptsize 5~625[/latex]
    [latex]\scriptsize 200[/latex] [latex]\scriptsize 5[/latex] [latex]\scriptsize 100[/latex] [latex]\scriptsize -37.2[/latex] [latex]\scriptsize -3~722.2[/latex] [latex]\scriptsize 10~000[/latex]
    Sums [latex]\scriptsize 900[/latex] [latex]\scriptsize 380[/latex] [latex]\scriptsize -14~475[/latex] [latex]\scriptsize 37~500[/latex]
    Mean [latex]\scriptsize 100[/latex] [latex]\scriptsize 42.2[/latex]

    Gradient:
    [latex]\scriptsize \begin{align*}b&=\displaystyle \frac{{\sum{{(x-\bar{x})(y-\bar{y})}}}}{{\sum{{{{{(x-\bar{x})}}^{2}}}}}}\\&=\displaystyle \frac{{-14\text{ }475}}{{37\text{ }500}}\\&=-0.386\end{align*}[/latex]
    y-intercept:
    [latex]\scriptsize \begin{align*}a&=\displaystyle \frac{{\sum{{y-b\sum{x}}}}}{n}=\bar{y}-b\bar{x}\\&=42.2-(-0.386)(100)\\&=42.2+38.6\\&=80.8\end{align*}[/latex]
    Regression equation: substituting for [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] in [latex]\scriptsize \hat{y}=a+bx[/latex]:
    [latex]\scriptsize \begin{align*}\hat{y}&=a+bx\\\hat{y}&=80.8-0.386x\end{align*}[/latex]
    .
    Check that the point [latex]\scriptsize (\bar{x},\text{ }\bar{y})=(100,42.2)[/latex] lies on the line.
    Substituting [latex]\scriptsize x=100[/latex] into the regression equation gives [latex]\scriptsize \hat{y}=80.8-0.386x=80.8-38.6=42.2[/latex], so this point lies on the line.

  3. .
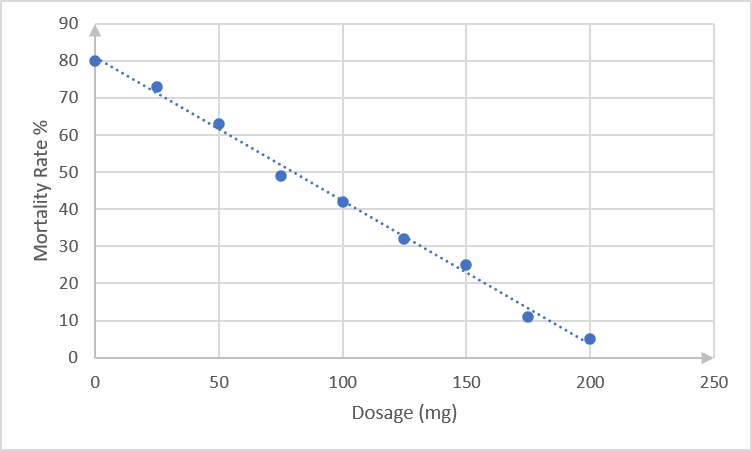
  4. To find the dosage for a [latex]\scriptsize 0\%[/latex] mortality rate, substitute [latex]\scriptsize \hat{y}=0[/latex] in the regression equation, therefore:
    [latex]\scriptsize \begin{align*}\hat{y}&=80.8-0.386x\\0.386x&=80.8\\x&=209.33\end{align*}[/latex]

Exercise 3.1

Question 1 follows on from exercise 2.1 number 3 of unit 2 in this subject outcome.

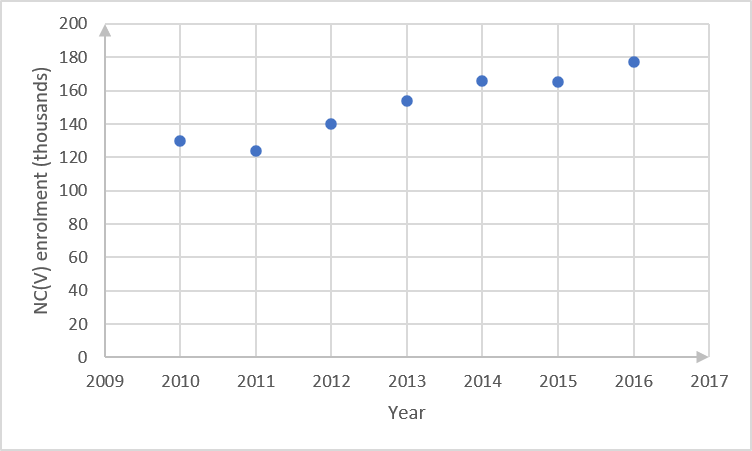
  1. The enrolment of learners for NC(V) programmes at TVET colleges was reported as follows:
    Year [latex]\scriptsize 2010[/latex] [latex]\scriptsize 2011[/latex] [latex]\scriptsize 2012[/latex] [latex]\scriptsize 2013[/latex] [latex]\scriptsize 2014[/latex] [latex]\scriptsize 2015[/latex] [latex]\scriptsize 2016[/latex]
    NC(V) enrolment (in thousands) [latex]\scriptsize 130[/latex] [latex]\scriptsize 124[/latex] [latex]\scriptsize 140[/latex] [latex]\scriptsize 154[/latex] [latex]\scriptsize 166[/latex] [latex]\scriptsize 165[/latex] [latex]\scriptsize 177[/latex]
    1. Draw a scatter plot of this data with the year on the horizontal axis and the enrolment on the vertical axis.
    2. Use the formulae for [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] to find the regression equation for the line of best fit.
    3. Draw the line of best fit on the scatter plot. Compare this line to the best fit line you drew in unit 2, exercise 2.1 question 3.
    4. According to the equation, what enrolment could be expected in the year [latex]\scriptsize 2022[/latex]?

Question 2 taken from Siyavula Grade 12 Mathematics Exercise 9-3

  1. For each of the following data sets:
    1. .
      [latex]\scriptsize x[/latex] [latex]\scriptsize 10[/latex] [latex]\scriptsize 4[/latex] [latex]\scriptsize 9[/latex] [latex]\scriptsize 11[/latex] [latex]\scriptsize 11[/latex] [latex]\scriptsize 6[/latex] [latex]\scriptsize 8[/latex] [latex]\scriptsize 18[/latex]
      [latex]\scriptsize y[/latex] [latex]\scriptsize 1[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize 6[/latex] [latex]\scriptsize 3[/latex] [latex]\scriptsize 9[/latex] [latex]\scriptsize 5[/latex] [latex]\scriptsize 9[/latex] [latex]\scriptsize 8[/latex]
    2. .
      [latex]\scriptsize x[/latex] [latex]\scriptsize 8[/latex] [latex]\scriptsize 12[/latex] [latex]\scriptsize 12[/latex] [latex]\scriptsize 7[/latex] [latex]\scriptsize 6[/latex] [latex]\scriptsize 14[/latex] [latex]\scriptsize 8[/latex] [latex]\scriptsize 14[/latex]
      [latex]\scriptsize y[/latex] [latex]\scriptsize -5[/latex] [latex]\scriptsize 4[/latex] [latex]\scriptsize 3[/latex] [latex]\scriptsize -3[/latex] [latex]\scriptsize -5[/latex] [latex]\scriptsize -6[/latex] [latex]\scriptsize -2[/latex] [latex]\scriptsize 0[/latex]
    3. .
      [latex]\scriptsize x[/latex] [latex]\scriptsize 1.9[/latex] [latex]\scriptsize 1.1[/latex] [latex]\scriptsize -1.5[/latex] [latex]\scriptsize 1.3[/latex] [latex]\scriptsize 0.95[/latex] [latex]\scriptsize 8.25[/latex] [latex]\scriptsize 10.6[/latex] [latex]\scriptsize 6.2[/latex]
      [latex]\scriptsize y[/latex] [latex]\scriptsize 7[/latex] [latex]\scriptsize 8.45[/latex] [latex]\scriptsize 0.9[/latex] [latex]\scriptsize 0.1[/latex] [latex]\scriptsize 2.45[/latex] [latex]\scriptsize 4.35[/latex] [latex]\scriptsize 2.2[/latex] [latex]\scriptsize 1.4[/latex]
      1. Draw a scatter plot of the data.
      2. Use a table to determine the values of [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] in order to find the least squares regression equation for each line of best fit. Round [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] off to two decimal places where necessary.
      3. Draw the line of best fit on the scatter plot.
      4. Use your equation in each case to predict the value of [latex]\scriptsize y[/latex] when [latex]\scriptsize x=25[/latex].

Question 3 follows on from question 3 of unit 2 assessment in this subject outcome

  1. A college assists learners to complete their national diplomas by negotiating with employers in the region with the aim of placing the learners for work experience. Over recent years they have tracked their engagements with employers against numbers of learners placed in work experience as follows:
    No. employers engaged [latex]\scriptsize 15[/latex] [latex]\scriptsize 45[/latex] [latex]\scriptsize 65[/latex] [latex]\scriptsize 35[/latex] [latex]\scriptsize 38[/latex] [latex]\scriptsize 25[/latex] [latex]\scriptsize 40[/latex] [latex]\scriptsize 30[/latex]
    No. learners placed [latex]\scriptsize 40[/latex] [latex]\scriptsize 90[/latex] [latex]\scriptsize 128[/latex] [latex]\scriptsize 90[/latex] [latex]\scriptsize 95[/latex] [latex]\scriptsize 60[/latex] [latex]\scriptsize 140[/latex] [latex]\scriptsize 75[/latex]
    1. Draw a scatter plot of the data.
    2. Use a table to determine the values of [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] in order to find the least squares regression equation for the line of best fit. Round [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] off to two decimal places where necessary.
    3. Draw the line of best fit on the scatter plot. Compare this line to the best fit line you drew in unit 2.
    4. Use the equation of the line of best fit to estimate the number of employers that would need to be engaged in order to place [latex]\scriptsize 175[/latex] learners in work placements.

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

  • How to determine the linear regression equation [latex]\scriptsize \hat{y}=a+bx[/latex] for a set of bivariate data.
  • How to use the regression line to predict the outcome of a given problem.

Unit 3: Assessment

Suggested time to complete: 55 minutes

See question 1 of unit 2 assessment; question adapted from NC(V) Mathematics Level 4 examination, November 2017

  1. A study was done to compare electricity usage of geysers that are inside or outside the house. The table below shows the electricity usage (in kilowatt hours) for equivalent water consumption for matched households that have geysers inside the house, and those with geysers outside the house. Nine houses of each type were considered in the study.
    Inside the house (kWh) [latex]\scriptsize 29[/latex] [latex]\scriptsize 31[/latex] [latex]\scriptsize 20[/latex] [latex]\scriptsize 40[/latex] [latex]\scriptsize 26[/latex] [latex]\scriptsize 39[/latex] [latex]\scriptsize 32[/latex] [latex]\scriptsize 34[/latex] [latex]\scriptsize 35[/latex]
    Outside the house (kWh) [latex]\scriptsize 19[/latex] [latex]\scriptsize 23[/latex] [latex]\scriptsize 13[/latex] [latex]\scriptsize 32[/latex] [latex]\scriptsize 17[/latex] [latex]\scriptsize 28[/latex] [latex]\scriptsize 25[/latex] [latex]\scriptsize 24[/latex] [latex]\scriptsize 28[/latex]
    1. Draw a scatter plot of the data.
    2. Using the information above, find the sample regression equation using the method of least squares.
    3. If the geyser fitted outside the house uses [latex]\scriptsize 40\text{kWh}[/latex], what will the usage be with the geyser inside the house?

Question 2 taken from NC(V) Mathematics Level 4 examination, November 2015

  1. ATA Consultants is a company that offers tuition for learners from grade 8 to grade 12. For the past [latex]\scriptsize 5[/latex] years they have distributed flyers to learners and have enrolled numbers of learners according to the table given below.
    Number of flyers distributed

    [latex]\scriptsize (x)[/latex]

    		 Number of learners enrolled

    [latex]\scriptsize (y)[/latex]
    [latex]\scriptsize 50[/latex] [latex]\scriptsize 15[/latex]
    [latex]\scriptsize 250[/latex] [latex]\scriptsize 45[/latex]
    [latex]\scriptsize 200[/latex] [latex]\scriptsize 40[/latex]
    [latex]\scriptsize 350[/latex] [latex]\scriptsize 65[/latex]
    [latex]\scriptsize 150[/latex] [latex]\scriptsize 35[/latex]
    1. Draw a scatter plot showing on the x-axis the number of flyers distributed and on the y-axis the number of learners enrolled.
    2. Using the information above find the simple regression equation by the method of least squares.
    3. Use the regression equation to determine the number of learners that would be enrolled if [latex]\scriptsize 500[/latex] flyers were sent out.

Question 3 taken from NC(V) Mathematics Level 4 examination, November 2019

  1. The data below shows the mathematics marks of ten learners at a college for the internal examinations and the external examinations.
    Internal examinations [latex]\scriptsize (x)[/latex] [latex]\scriptsize 80[/latex] [latex]\scriptsize 68[/latex] [latex]\scriptsize 94[/latex] [latex]\scriptsize 72[/latex] [latex]\scriptsize 74[/latex] [latex]\scriptsize 83[/latex] [latex]\scriptsize 56[/latex] [latex]\scriptsize 68[/latex] [latex]\scriptsize 65[/latex] [latex]\scriptsize 75[/latex]
    External examinations [latex]\scriptsize (x)[/latex] [latex]\scriptsize 72[/latex] [latex]\scriptsize 71[/latex] [latex]\scriptsize 96[/latex] [latex]\scriptsize 77[/latex] [latex]\scriptsize 82[/latex] [latex]\scriptsize 72[/latex] [latex]\scriptsize 58[/latex] [latex]\scriptsize 83[/latex] [latex]\scriptsize 78[/latex] [latex]\scriptsize 80[/latex]
    1. Make a scatter plot of the marks in the above table on an x-y plane, with each axis showing values from [latex]\scriptsize 50[/latex] to [latex]\scriptsize 96[/latex].
    2. Calculate the equation of the least squares regression line for the data. No marks will be awarded if answers are taken directly from a calculator. Complete all the calculations in a table that shows
      EITHER (x) (y) xy x2
      OR (x) (y) [latex]\scriptsize (x-\bar{x})(y-\bar{y})[/latex] [latex]\scriptsize {{(x-\bar{x})}^{2}}[/latex]
    3. Draw the least squares regression line on the x-y plane.
    4. Calculate the predicted final examination mark for a learner who scores [latex]\scriptsize 70[/latex] in the internal examination.

See unit 2 assessment question 2

  1. Tobacco smoking is still one of the world’s largest health problems, although prevalence of smoking is generally decreasing. The table below shows numbers of deaths (in thousands) in South Africa from smoking, in recent years.
    Year [latex]\scriptsize 2010[/latex] [latex]\scriptsize 2011[/latex] [latex]\scriptsize 2012[/latex] [latex]\scriptsize 2013[/latex] [latex]\scriptsize 2014[/latex] [latex]\scriptsize 2015[/latex] [latex]\scriptsize 2016[/latex] [latex]\scriptsize 2017[/latex]
    Deaths [latex]\scriptsize ('000)[/latex] [latex]\scriptsize 38.0[/latex] [latex]\scriptsize 35.8[/latex] [latex]\scriptsize 34.1[/latex] [latex]\scriptsize 32.6[/latex] [latex]\scriptsize 31.8[/latex] [latex]\scriptsize 31.5[/latex] [latex]\scriptsize 31.3[/latex] [latex]\scriptsize 29.9[/latex]
    1. Draw a scatter plot of the data.
    2. Calculate the equation of the least squares regression line for the data.
    3. Draw the least squares regression line into the graph of the scatter plot.
    4. Draw the line of best fit on the scatter plot. Compare this line to the best fit line you drew in unit 2.
    5. Use the regression equation to calculate the number of deaths from smoking predicted for [latex]\scriptsize 2022[/latex].

The full solutions are at the end of the unit.

Unit 3: Solutions

Exercise 3.1

  1. .
    1. .
    2. .
      Year

      [latex]\scriptsize x[/latex]

      		 Enrolment

      [latex]\scriptsize ( `000) y[/latex]

      		 [latex]\scriptsize x-\bar{x}[/latex] [latex]\scriptsize y-\bar{y}[/latex] [latex]\scriptsize (x-\bar{x})(y-\bar{y})[/latex] [latex]\scriptsize (x-\bar{x})^2[/latex]
      [latex]\scriptsize 2010[/latex] [latex]\scriptsize 130[/latex] [latex]\scriptsize -3[/latex] [latex]\scriptsize -20.86[/latex] [latex]\scriptsize 62.58[/latex] [latex]\scriptsize 9[/latex]
      [latex]\scriptsize 2011[/latex] [latex]\scriptsize 124[/latex] [latex]\scriptsize -2[/latex] [latex]\scriptsize -26.86[/latex] [latex]\scriptsize 53.72[/latex] [latex]\scriptsize 4[/latex]
      [latex]\scriptsize 2012[/latex] [latex]\scriptsize 140[/latex] [latex]\scriptsize -1[/latex] [latex]\scriptsize -10.86[/latex] [latex]\scriptsize 10.86[/latex] [latex]\scriptsize 1[/latex]
      [latex]\scriptsize 2013[/latex] [latex]\scriptsize 154[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize 3.14[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize 0[/latex]
      [latex]\scriptsize 2014[/latex] [latex]\scriptsize 166[/latex] [latex]\scriptsize 1[/latex] [latex]\scriptsize 15.14[/latex] [latex]\scriptsize 15.14[/latex] [latex]\scriptsize 1[/latex]
      [latex]\scriptsize 2015[/latex] [latex]\scriptsize 165[/latex] [latex]\scriptsize 2[/latex] [latex]\scriptsize 14.14[/latex] [latex]\scriptsize 28.28[/latex] [latex]\scriptsize 4[/latex]
      [latex]\scriptsize 2016[/latex] [latex]\scriptsize 177[/latex] [latex]\scriptsize 3[/latex] [latex]\scriptsize 26.14[/latex] [latex]\scriptsize 78.42[/latex] [latex]\scriptsize 9[/latex]
      Sums [latex]\scriptsize 14~091[/latex] [latex]\scriptsize 1~056[/latex] [latex]\scriptsize 249[/latex] [latex]\scriptsize 28[/latex]
      Mean [latex]\scriptsize 2~013[/latex] [latex]\scriptsize 150.86[/latex]

      Gradient:
      [latex]\scriptsize \begin{align*}b&=\displaystyle \frac{{\sum{{(x-\bar{x})(y-\bar{y})}}}}{{\sum{{{{{(x-\bar{x})}}^{2}}}}}}\\&=\displaystyle \frac{{249}}{{28}}\\&=8.89\end{align*}[/latex]
      y-intercept:
      [latex]\scriptsize \begin{align*}a&=\bar{y}-b\bar{x}\\&=150.86-(8.89)(2013)\\&=150.86-17\text{ }895.57\\&=-17\text{ 744}.71\end{align*}[/latex]
      Regression equation: substituting for [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] in [latex]\scriptsize \hat{y}=a+bx[/latex]:
      [latex]\scriptsize \begin{align*}\hat{y}&=a+bx\\\hat{y}&=-17\text{ 744}.71+8.89x\end{align*}[/latex]

    3. .
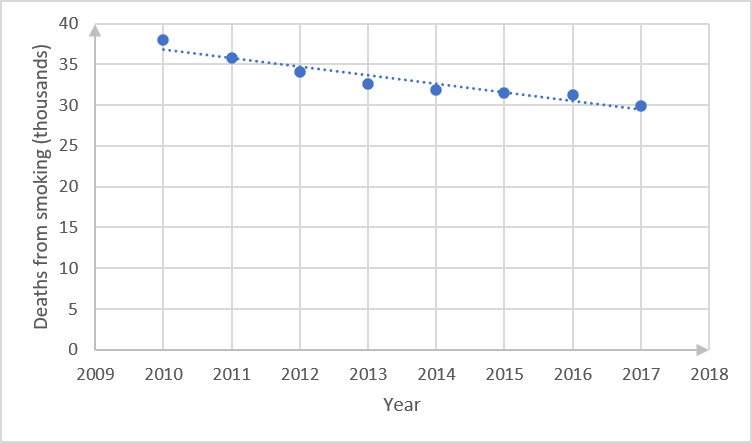
    4. To find enrolment expected in [latex]\scriptsize 2022[/latex], substitute this value into the regression equation:
      [latex]\scriptsize \begin{align*}\hat{y}&=-17\text{ 744}.71+8.89x\\\hat{y}&=-17\text{ 744}.71+8.89(2022)\\&=-17\text{ 744}\text{.71}+17\text{ }975.58\\&=230.87\end{align*}[/latex]
      So, enrolment in [latex]\scriptsize 2022[/latex] is expected to be [latex]\scriptsize 230.87[/latex] thousands, or [latex]\scriptsize 230\text{ 870}[/latex] learners.
  2. .
    1. .
      [latex]\scriptsize x[/latex] [latex]\scriptsize 10[/latex] [latex]\scriptsize 4[/latex] [latex]\scriptsize 9[/latex] [latex]\scriptsize 11[/latex] [latex]\scriptsize 11[/latex] [latex]\scriptsize 6[/latex] [latex]\scriptsize 8[/latex] [latex]\scriptsize 18[/latex]
      [latex]\scriptsize y[/latex] [latex]\scriptsize 1[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize 6[/latex] [latex]\scriptsize 3[/latex] [latex]\scriptsize 9[/latex] [latex]\scriptsize 5[/latex] [latex]\scriptsize 9[/latex] [latex]\scriptsize 8[/latex]
      1. .
      2. .
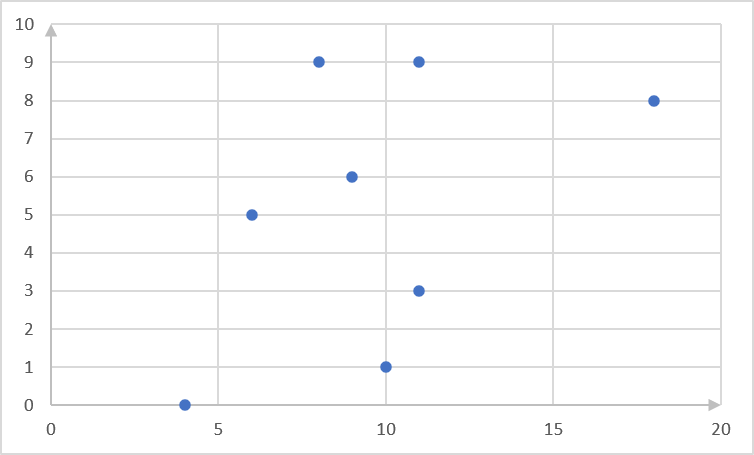
        [latex]\scriptsize x[/latex] [latex]\scriptsize y[/latex] [latex]\scriptsize x-\bar{x}[/latex] [latex]\scriptsize y-\bar{y}[/latex] [latex]\scriptsize (x-\bar{x})(y-\bar{y})[/latex] [latex]\scriptsize (x-\bar{x})^2[/latex]
        [latex]\scriptsize 10[/latex] [latex]\scriptsize 1[/latex] [latex]\scriptsize 0.37[/latex] [latex]\scriptsize -4.13[/latex] [latex]\scriptsize -1.53[/latex] [latex]\scriptsize 0.14[/latex]
        [latex]\scriptsize 4[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -5.63[/latex] [latex]\scriptsize -5.13[/latex] [latex]\scriptsize 28.88[/latex] [latex]\scriptsize 31.70[/latex]
        [latex]\scriptsize 9[/latex] [latex]\scriptsize 6[/latex] [latex]\scriptsize -0.63[/latex] [latex]\scriptsize 0.87[/latex] [latex]\scriptsize -0.55[/latex] [latex]\scriptsize 0.40[/latex]
        [latex]\scriptsize 11[/latex] [latex]\scriptsize 3[/latex] [latex]\scriptsize 1.37[/latex] [latex]\scriptsize -2.13[/latex] [latex]\scriptsize -2.92[/latex] [latex]\scriptsize 1.88[/latex]
        [latex]\scriptsize 11[/latex] [latex]\scriptsize 9[/latex] [latex]\scriptsize 1.37[/latex] [latex]\scriptsize 3.87[/latex] [latex]\scriptsize 5.30[/latex] [latex]\scriptsize 1.88[/latex]
        [latex]\scriptsize 6[/latex] [latex]\scriptsize 5[/latex] [latex]\scriptsize -3.63[/latex] [latex]\scriptsize -0.13[/latex] [latex]\scriptsize 0.47[/latex] [latex]\scriptsize 13.18[/latex]
        [latex]\scriptsize 8[/latex] [latex]\scriptsize 9[/latex] [latex]\scriptsize -1.63[/latex] [latex]\scriptsize 3.87[/latex] [latex]\scriptsize -6.31[/latex] [latex]\scriptsize 2.66[/latex]
        [latex]\scriptsize 18[/latex] [latex]\scriptsize 8[/latex] [latex]\scriptsize 8.37[/latex] [latex]\scriptsize 2.87[/latex] [latex]\scriptsize 24.02[/latex] [latex]\scriptsize 70.06[/latex]
        Sums [latex]\scriptsize 77[/latex] [latex]\scriptsize 41[/latex] [latex]\scriptsize 50.41[/latex] [latex]\scriptsize 121.9[/latex]
        Mean [latex]\scriptsize 9.63[/latex] [latex]\scriptsize 5.13[/latex]

        Gradient:
        [latex]\scriptsize \begin{align*}b&=\displaystyle \frac{{\sum{{(x-\bar{x})(y-\bar{y})}}}}{{\sum{{{{{(x-\bar{x})}}^{2}}}}}}\\&=\displaystyle \frac{{50.41}}{{121.9}}\\&=0.41\end{align*}[/latex]
        y-intercept:
        [latex]\scriptsize \begin{align*}a&=\bar{y}-b\bar{x}\\&=5.13-(0.13)(9.63)\\&=5.13-1.25\\&=3.88\end{align*}[/latex]
        Regression equation: substituting for [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] in [latex]\scriptsize \hat{y}=a+bx[/latex]:
        [latex]\scriptsize \begin{align*}\hat{y}&=a+bx\\\hat{y}&=3.88+0.41x\end{align*}[/latex]

      3. .
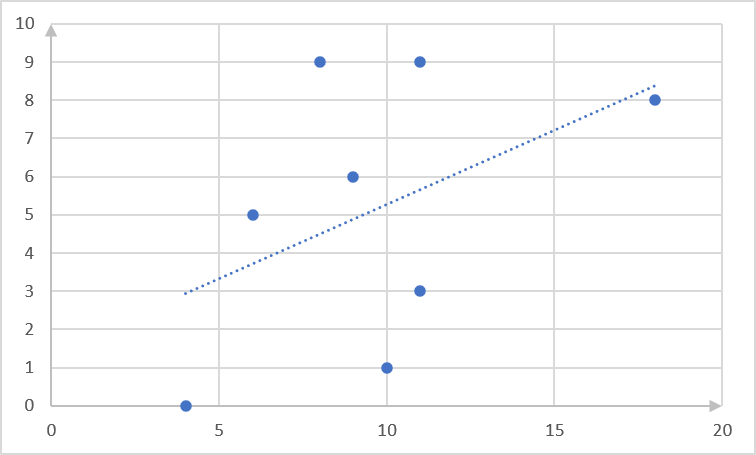
      4. To find [latex]\scriptsize y\text{-value}[/latex] when [latex]\scriptsize x=25[/latex], substitute this value into the regression equation:
        [latex]\scriptsize \begin{align*}\hat{y}&=3.88+0.41x\\\hat{y}&=3.88+0.41(25)\\&=3.88+10.25\\&=14.13\end{align*}[/latex]
    2. .
      [latex]\scriptsize x[/latex] [latex]\scriptsize 8[/latex] [latex]\scriptsize 12[/latex] [latex]\scriptsize 12[/latex] [latex]\scriptsize 7[/latex] [latex]\scriptsize 6[/latex] [latex]\scriptsize 14[/latex] [latex]\scriptsize 8[/latex] [latex]\scriptsize 14[/latex]
      [latex]\scriptsize y[/latex] [latex]\scriptsize -5[/latex] [latex]\scriptsize 4[/latex] [latex]\scriptsize 3[/latex] [latex]\scriptsize -3[/latex] [latex]\scriptsize -5[/latex] [latex]\scriptsize -6[/latex] [latex]\scriptsize -2[/latex] [latex]\scriptsize 0[/latex]
      1. .
      2. .
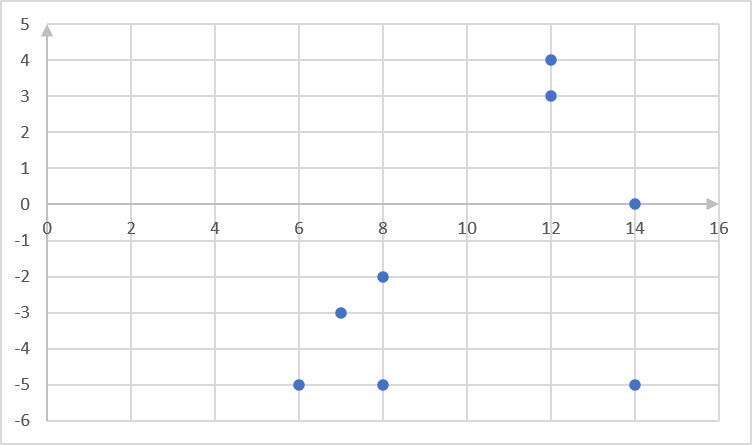
        [latex]\scriptsize x[/latex] [latex]\scriptsize y[/latex] [latex]\scriptsize x-\bar{x}[/latex] [latex]\scriptsize y-\bar{y}[/latex] [latex]\scriptsize (x-\bar{x})(y-\bar{y})[/latex] [latex]\scriptsize (x-\bar{x})^2[/latex]
        [latex]\scriptsize 8[/latex] [latex]\scriptsize -5[/latex] [latex]\scriptsize -2.13[/latex] [latex]\scriptsize -3.25[/latex] [latex]\scriptsize 6.92[/latex] [latex]\scriptsize 4.54[/latex]
        [latex]\scriptsize 12[/latex] [latex]\scriptsize 4[/latex] [latex]\scriptsize 1.87[/latex] [latex]\scriptsize 2.25[/latex] [latex]\scriptsize 4.21[/latex] [latex]\scriptsize 3.50[/latex]
        [latex]\scriptsize 12[/latex] [latex]\scriptsize 3[/latex] [latex]\scriptsize 1.87[/latex] [latex]\scriptsize 4.75[/latex] [latex]\scriptsize 8.88[/latex] [latex]\scriptsize 3.50[/latex]
        [latex]\scriptsize 7[/latex] [latex]\scriptsize -3[/latex] [latex]\scriptsize -3.13[/latex] [latex]\scriptsize -1.25[/latex] [latex]\scriptsize 3.91[/latex] [latex]\scriptsize 9.80[/latex]
        [latex]\scriptsize 6[/latex] [latex]\scriptsize -5[/latex] [latex]\scriptsize -4.13[/latex] [latex]\scriptsize -4.5[/latex] [latex]\scriptsize 18.59[/latex] [latex]\scriptsize 17.06[/latex]
        [latex]\scriptsize 14[/latex] [latex]\scriptsize -6[/latex] [latex]\scriptsize 3.87[/latex] [latex]\scriptsize -4.25[/latex] [latex]\scriptsize -16.45[/latex] [latex]\scriptsize 14.98[/latex]
        [latex]\scriptsize 8[/latex] [latex]\scriptsize -2[/latex] [latex]\scriptsize -2.13[/latex] [latex]\scriptsize -0.25[/latex] [latex]\scriptsize 0.53[/latex] [latex]\scriptsize 4.54[/latex]
        [latex]\scriptsize 14[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize 3.87[/latex] [latex]\scriptsize 1.75[/latex] [latex]\scriptsize 6.77[/latex] [latex]\scriptsize 14.98[/latex]
        Sums [latex]\scriptsize 81[/latex] [latex]\scriptsize -14[/latex] [latex]\scriptsize 33.36[/latex] [latex]\scriptsize 72.9[/latex]
        Mean [latex]\scriptsize 10.13[/latex] [latex]\scriptsize -1.75[/latex]

        Gradient:
        [latex]\scriptsize \begin{align*}b&=\displaystyle \frac{{\sum{{(x-\bar{x})(y-\bar{y})}}}}{{\sum{{{{{(x-\bar{x})}}^{2}}}}}}\\&=\displaystyle \frac{{33.36}}{{72.9}}\\&=0.46\end{align*}[/latex]
        y-intercept:
        [latex]\scriptsize \begin{align*}a&=\bar{y}-b\bar{x}\\&=-1.75-(0.46)(10.13)\\&=-1.75-4.66\\&=-6.41\end{align*}[/latex]
        Regression equation: substituting for [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] in [latex]\scriptsize \hat{y}=a+bx[/latex]:
        [latex]\scriptsize \begin{align*}\hat{y}&=a+bx\\\hat{y}&=-6.41+0.46x\end{align*}[/latex]

      3. .
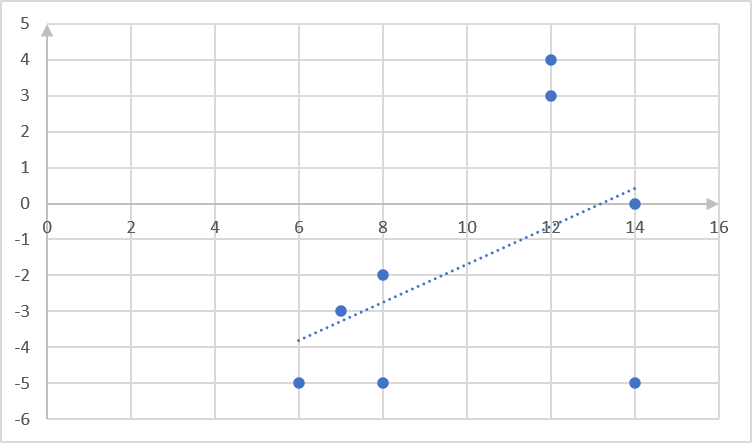
      4. To find [latex]\scriptsize y\text{-value}[/latex] when [latex]\scriptsize x=25[/latex], substitute this value into the regression equation:
        [latex]\scriptsize \begin{align*}\hat{y}&=-6.41+0.46x\\\hat{y}&=-6.41+0.46(25)\\&=-6.41+11.5\\&=5.09\end{align*}[/latex]
    3. .
      [latex]\scriptsize x[/latex] [latex]\scriptsize 1.9[/latex] [latex]\scriptsize 1.1[/latex] [latex]\scriptsize -1.5[/latex] [latex]\scriptsize 1.3[/latex] [latex]\scriptsize 0.95[/latex] [latex]\scriptsize 8.25[/latex] [latex]\scriptsize 10.6[/latex] [latex]\scriptsize 6.2[/latex]
      [latex]\scriptsize y[/latex] [latex]\scriptsize 7[/latex] [latex]\scriptsize 8.45[/latex] [latex]\scriptsize 0.9[/latex] [latex]\scriptsize 0.1[/latex] [latex]\scriptsize 2.45[/latex] [latex]\scriptsize 4.35[/latex] [latex]\scriptsize 2.2[/latex] [latex]\scriptsize 1.4[/latex]
      1. .
      2. .
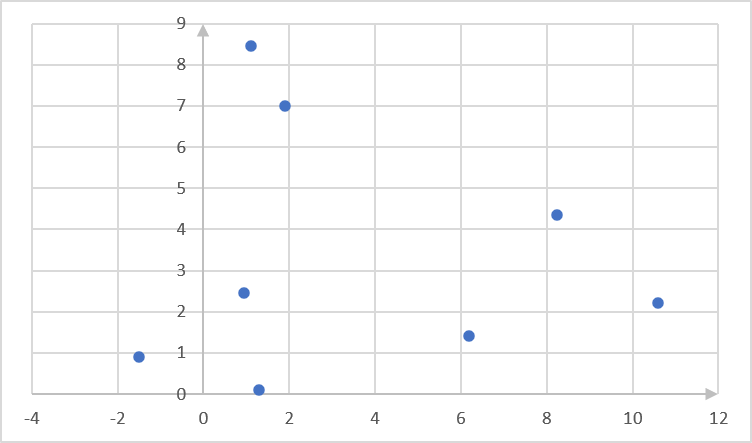
        [latex]\scriptsize x[/latex] [latex]\scriptsize y[/latex] [latex]\scriptsize x-\bar{x}[/latex] [latex]\scriptsize y-\bar{y}[/latex] [latex]\scriptsize (x-\bar{x})(y-\bar{y})[/latex] [latex]\scriptsize (x-\bar{x})^2[/latex]
        [latex]\scriptsize 1.9[/latex] [latex]\scriptsize 7[/latex] [latex]\scriptsize -1.7[/latex] [latex]\scriptsize 3.64[/latex] [latex]\scriptsize -6.19[/latex] [latex]\scriptsize 2.89[/latex]
        [latex]\scriptsize 1.1[/latex] [latex]\scriptsize 8.45[/latex] [latex]\scriptsize -2.5[/latex] [latex]\scriptsize 5.09[/latex] [latex]\scriptsize -12.73[/latex] [latex]\scriptsize 6.25[/latex]
        [latex]\scriptsize -1.5[/latex] [latex]\scriptsize 0.9[/latex] [latex]\scriptsize -5.1[/latex] [latex]\scriptsize -2.46[/latex] [latex]\scriptsize 12.55[/latex] [latex]\scriptsize 26.01[/latex]
        [latex]\scriptsize 1.3[/latex] [latex]\scriptsize 0.1[/latex] [latex]\scriptsize -2.3[/latex] [latex]\scriptsize -3.26[/latex] [latex]\scriptsize 7.50[/latex] [latex]\scriptsize 5.29[/latex]
        [latex]\scriptsize 0.95[/latex] [latex]\scriptsize 2.45[/latex] [latex]\scriptsize -2.65[/latex] [latex]\scriptsize -0.91[/latex] [latex]\scriptsize 2.41[/latex] [latex]\scriptsize 7.02[/latex]
        [latex]\scriptsize 8.25[/latex] [latex]\scriptsize 4.35[/latex] [latex]\scriptsize 4.65[/latex] [latex]\scriptsize 0.99[/latex] [latex]\scriptsize 4.60[/latex] [latex]\scriptsize 21.62[/latex]
        [latex]\scriptsize 10.6[/latex] [latex]\scriptsize 2.2[/latex] [latex]\scriptsize 7[/latex] [latex]\scriptsize -1.16[/latex] [latex]\scriptsize -8.12[/latex] [latex]\scriptsize 49[/latex]
        [latex]\scriptsize 6.2[/latex] [latex]\scriptsize 1.4[/latex] [latex]\scriptsize 2.6[/latex] [latex]\scriptsize -1.96[/latex] [latex]\scriptsize -5.10[/latex] [latex]\scriptsize 6.76[/latex]
        Sums [latex]\scriptsize 28.8[/latex] [latex]\scriptsize 26.85[/latex] [latex]\scriptsize -5.08[/latex] [latex]\scriptsize 124.84[/latex]
        Mean [latex]\scriptsize 3.6[/latex] [latex]\scriptsize 3.36[/latex]

        Gradient:
        [latex]\scriptsize \begin{align*}b&=\displaystyle \frac{{\sum{{(x-\bar{x})(y-\bar{y})}}}}{{\sum{{{{{(x-\bar{x})}}^{2}}}}}}\\&=\displaystyle \frac{{-5.08}}{{124.84}}\\&=-0.04\end{align*}[/latex]
        y-intercept:
        [latex]\scriptsize \begin{align*}a&=\bar{y}-b\bar{x}\\&=3.36-(-0.04)(3.6)\\&=3.36+0.144\\&=3.50\end{align*}[/latex]
        Regression equation: substituting for [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] in [latex]\scriptsize \hat{y}=a+bx[/latex]:
        [latex]\scriptsize \begin{align*}\hat{y}&=a+bx\\\hat{y}&=3.5-0.04x\end{align*}[/latex]

      3. .
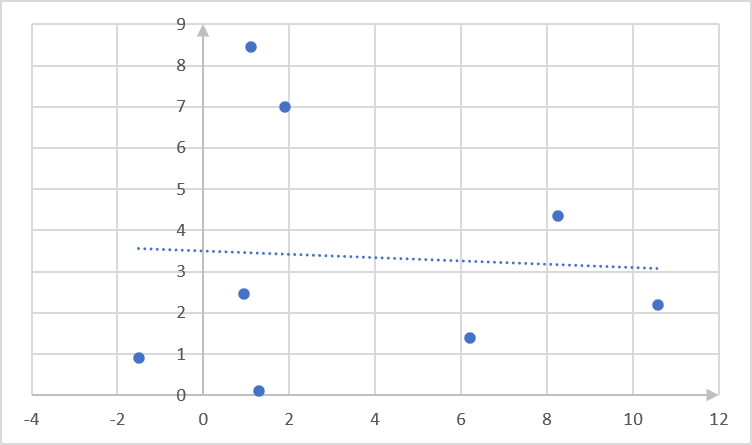
      4. To find [latex]\scriptsize y\text{-value}[/latex] when [latex]\scriptsize x=25[/latex], substitute this value into the regression equation:
        [latex]\scriptsize \begin{align*}\hat{y}&=3.5-0.04x\\\hat{y}&=3.5-0.04(25)\\&=3.5-1\\&=2.5\end{align*}[/latex]
  3. .
    No. employers engaged [latex]\scriptsize 15[/latex] [latex]\scriptsize 45[/latex] [latex]\scriptsize 65[/latex] [latex]\scriptsize 35[/latex] [latex]\scriptsize 38[/latex] [latex]\scriptsize 25[/latex] [latex]\scriptsize 40[/latex] [latex]\scriptsize 30[/latex]
    No. learners placed [latex]\scriptsize 40[/latex] [latex]\scriptsize 90[/latex] [latex]\scriptsize 128[/latex] [latex]\scriptsize 90[/latex] [latex]\scriptsize 95[/latex] [latex]\scriptsize 60[/latex] [latex]\scriptsize 140[/latex] [latex]\scriptsize 75[/latex]
    1. .
    2. .
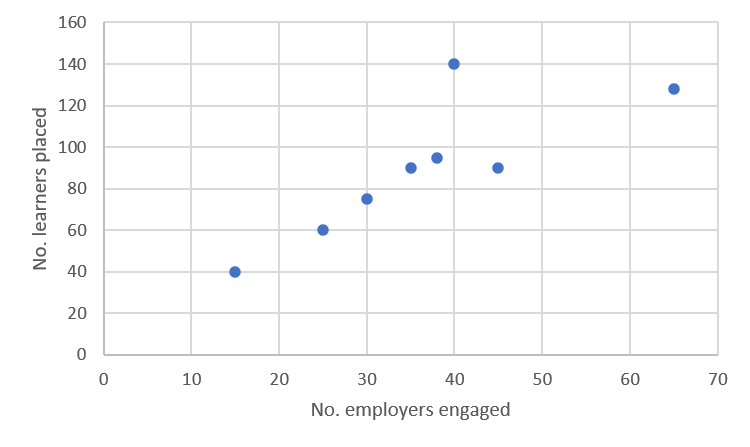
      No. employers engaged

      [latex]\scriptsize x[/latex]

      		 No. learners placed

      [latex]\scriptsize y[/latex]

      		 [latex]\scriptsize x-\bar{x}[/latex] [latex]\scriptsize y-\bar{y}[/latex] [latex]\scriptsize (x-\bar{x})(y-\bar{y})[/latex] [latex]\scriptsize (x-\bar{x})^2[/latex]
      [latex]\scriptsize 15[/latex] [latex]\scriptsize 40[/latex] [latex]\scriptsize -21.63[/latex] [latex]\scriptsize -49.75[/latex] [latex]\scriptsize 1~076.09[/latex] [latex]\scriptsize 467.86[/latex]
      [latex]\scriptsize 45[/latex] [latex]\scriptsize 90[/latex] [latex]\scriptsize 8.37[/latex] [latex]\scriptsize 0.25[/latex] [latex]\scriptsize 2.09[/latex] [latex]\scriptsize 70.06[/latex]
      [latex]\scriptsize 65[/latex] [latex]\scriptsize 128[/latex] [latex]\scriptsize 28.37[/latex] [latex]\scriptsize 38.25[/latex] [latex]\scriptsize 1~085.15[/latex] [latex]\scriptsize 804.86[/latex]
      [latex]\scriptsize 35[/latex] [latex]\scriptsize 90[/latex] [latex]\scriptsize -1.63[/latex] [latex]\scriptsize 0.25[/latex] [latex]\scriptsize -0.41[/latex] [latex]\scriptsize 2.66[/latex]
      [latex]\scriptsize 38[/latex] [latex]\scriptsize 95[/latex] [latex]\scriptsize 1.37[/latex] [latex]\scriptsize 5.25[/latex] [latex]\scriptsize 7.19[/latex] [latex]\scriptsize 1.88[/latex]
      [latex]\scriptsize 25[/latex] [latex]\scriptsize 60[/latex] [latex]\scriptsize -11.63[/latex] [latex]\scriptsize -29.75[/latex] [latex]\scriptsize 345.99[/latex] [latex]\scriptsize 135.26[/latex]
      [latex]\scriptsize 40[/latex] [latex]\scriptsize 140[/latex] [latex]\scriptsize 3.37[/latex] [latex]\scriptsize 50.25[/latex] [latex]\scriptsize 169.34[/latex] [latex]\scriptsize 11.36[/latex]
      [latex]\scriptsize 30[/latex] [latex]\scriptsize 75[/latex] [latex]\scriptsize -6.63[/latex] [latex]\scriptsize -14.75[/latex] [latex]\scriptsize 97.79[/latex] [latex]\scriptsize 43.96[/latex]
      Sums [latex]\scriptsize 293[/latex] [latex]\scriptsize 718[/latex] [latex]\scriptsize 2~783.23[/latex] [latex]\scriptsize 1~537.9[/latex]
      Mean [latex]\scriptsize 36.63[/latex] [latex]\scriptsize 89.75[/latex]

      Gradient:
      [latex]\scriptsize \begin{align*}b&=\displaystyle \frac{{\sum{{(x-\bar{x})(y-\bar{y})}}}}{{\sum{{{{{(x-\bar{x})}}^{2}}}}}}\\&=\displaystyle \frac{{2\text{ }783.23}}{{1\text{ }537.9}}\\&=1.81\end{align*}[/latex]
      y-intercept:
      [latex]\scriptsize \begin{align*}a&=\bar{y}-b\bar{x}\\&=89.75-(1.81)(36.63)\\&=89.75-66.30\\&=23.45\end{align*}[/latex]
      Regression equation: substituting for [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] in [latex]\scriptsize \hat{y}=a+bx[/latex]:
      [latex]\scriptsize \begin{align*}\hat{y}&=a+bx\\\hat{y}&=23.45+1.81x\end{align*}[/latex]

    3. .
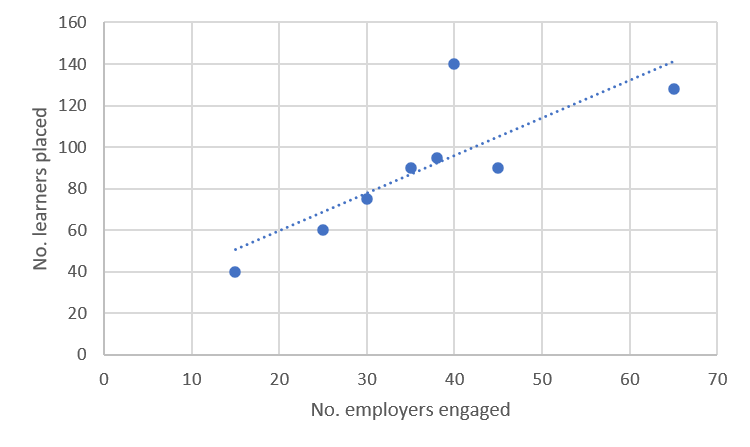
    4. To find [latex]\scriptsize x\text{-value}[/latex] when [latex]\scriptsize y=175[/latex], substitute this value into the regression equation:
      [latex]\scriptsize \begin{align*}\hat{y}&=23.45+1.81x\\175&=23.45+1.81x\\1.81x&=175-23.45\\x&=\displaystyle \frac{{151.55}}{{1.81}}\\&=83.73\end{align*}[/latex]
      At the current rate, approximately [latex]\scriptsize 84[/latex] employers would need to be engaged in order to find work placements for [latex]\scriptsize 175[/latex] learners.

Back to Exercise 3.1

Unit 3: Assessment

  1. .
    Inside the house (kWh) [latex]\scriptsize 29[/latex] [latex]\scriptsize 31[/latex] [latex]\scriptsize 20[/latex] [latex]\scriptsize 40[/latex] [latex]\scriptsize 26[/latex] [latex]\scriptsize 39[/latex] [latex]\scriptsize 32[/latex] [latex]\scriptsize 34[/latex] [latex]\scriptsize 35[/latex]
    Outside the house (kWh) [latex]\scriptsize 19[/latex] [latex]\scriptsize 23[/latex] [latex]\scriptsize 13[/latex] [latex]\scriptsize 32[/latex] [latex]\scriptsize 17[/latex] [latex]\scriptsize 28[/latex] [latex]\scriptsize 25[/latex] [latex]\scriptsize 24[/latex] [latex]\scriptsize 28[/latex]
    1. .
    2. .
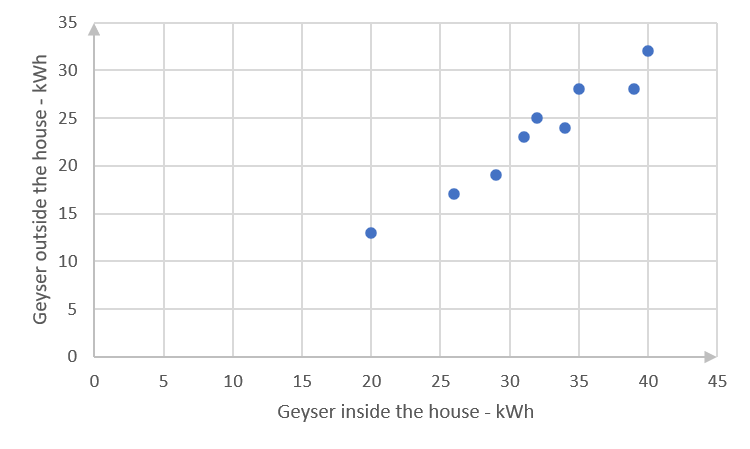
      Inside the house

      [latex]\scriptsize x[/latex]

      		 Outside the house

      [latex]\scriptsize y[/latex]

      		 [latex]\scriptsize x-\bar{x}[/latex] [latex]\scriptsize y-\bar{y}[/latex] [latex]\scriptsize (x-\bar{x})(y-\bar{y})[/latex] [latex]\scriptsize (x-\bar{x})^2[/latex]
      [latex]\scriptsize 29[/latex] [latex]\scriptsize 19[/latex] [latex]\scriptsize -2.78[/latex] [latex]\scriptsize -4.22[/latex] [latex]\scriptsize 11.73[/latex] [latex]\scriptsize 7.73[/latex]
      [latex]\scriptsize 31[/latex] [latex]\scriptsize 23[/latex] [latex]\scriptsize -0.78[/latex] [latex]\scriptsize -0.22[/latex] [latex]\scriptsize 0.17[/latex] [latex]\scriptsize 0.61[/latex]
      [latex]\scriptsize 20[/latex] [latex]\scriptsize 13[/latex] [latex]\scriptsize -11.78[/latex] [latex]\scriptsize -10.22[/latex] [latex]\scriptsize 120.39[/latex] [latex]\scriptsize 138.77[/latex]
      [latex]\scriptsize 40[/latex] [latex]\scriptsize 32[/latex] [latex]\scriptsize 8.22[/latex] [latex]\scriptsize 8.78[/latex] [latex]\scriptsize 72.17[/latex] [latex]\scriptsize 67.57[/latex]
      [latex]\scriptsize 26[/latex] [latex]\scriptsize 17[/latex] [latex]\scriptsize -5.78[/latex] [latex]\scriptsize -6.22[/latex] [latex]\scriptsize 35.95[/latex] [latex]\scriptsize 33.41[/latex]
      [latex]\scriptsize 39[/latex] [latex]\scriptsize 28[/latex] [latex]\scriptsize 7.22[/latex] [latex]\scriptsize 4.78[/latex] [latex]\scriptsize 34.51[/latex] [latex]\scriptsize 52.13[/latex]
      [latex]\scriptsize 32[/latex] [latex]\scriptsize 25[/latex] [latex]\scriptsize 0.22[/latex] [latex]\scriptsize 1.78[/latex] [latex]\scriptsize 0.39[/latex] [latex]\scriptsize 0.05[/latex]
      [latex]\scriptsize 34[/latex] [latex]\scriptsize 24[/latex] [latex]\scriptsize 2.22[/latex] [latex]\scriptsize 0.78[/latex] [latex]\scriptsize 1.73[/latex] [latex]\scriptsize 4.93[/latex]
      [latex]\scriptsize 35[/latex] [latex]\scriptsize 28[/latex] [latex]\scriptsize 3.22[/latex] [latex]\scriptsize 4.78[/latex] [latex]\scriptsize 15.39[/latex] [latex]\scriptsize 10.37[/latex]
      Sums [latex]\scriptsize 286[/latex] [latex]\scriptsize 209[/latex] [latex]\scriptsize -0.02[/latex] [latex]\scriptsize 0.02[/latex] [latex]\scriptsize 292.43[/latex] [latex]\scriptsize 315.57[/latex]
      Mean [latex]\scriptsize 31.78[/latex] [latex]\scriptsize 23.22[/latex]

      Gradient:
      [latex]\scriptsize \begin{align*}b&=\displaystyle \frac{{\sum{{(x-\bar{x})(y-\bar{y})}}}}{{\sum{{{{{(x-\bar{x})}}^{2}}}}}}\\&=\displaystyle \frac{{292.43}}{{315.57}}\\&=0.93\end{align*}[/latex]
      y-intercept:
      [latex]\scriptsize \begin{align*}a&=\bar{y}-b\bar{x}\\&=23.22-(0.93)(31.78)\\&=23.22-29.56\\&=-6.34\end{align*}[/latex]
      Regression equation: substituting for [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] in [latex]\scriptsize \hat{y}=a+bx[/latex]:
      [latex]\scriptsize \begin{align*}\hat{y}&=a+bx\\\hat{y}&=-6.34+0.93x\end{align*}[/latex]

    3. To find the electricity usage inside the house when the outside usage is [latex]\scriptsize 40\text{kWh}[/latex], substitute into the equation:
      [latex]\scriptsize \begin{align*}\hat{y}&=-6.34+0.93x\\0.93x&=6.34+\hat{y}\\x&=\displaystyle \frac{{6.34+40}}{{0.93}}\\x&=49.83\end{align*}[/latex]
      According to the regression equation, if the geyser outside the house uses [latex]\scriptsize 40\text{kWh}[/latex], the geyser inside the house will use [latex]\scriptsize 49.83\text{kWh}[/latex].
  2. .
    Number of flyers distributed

    [latex]\scriptsize (x)[/latex]

    		 Number of learners enrolled

    [latex]\scriptsize (y)[/latex]
    [latex]\scriptsize 50[/latex] [latex]\scriptsize 15[/latex]
    [latex]\scriptsize 250[/latex] [latex]\scriptsize 45[/latex]
    [latex]\scriptsize 200[/latex] [latex]\scriptsize 40[/latex]
    [latex]\scriptsize 350[/latex] [latex]\scriptsize 65[/latex]
    [latex]\scriptsize 150[/latex] [latex]\scriptsize 35[/latex]
    1. .
    2. .
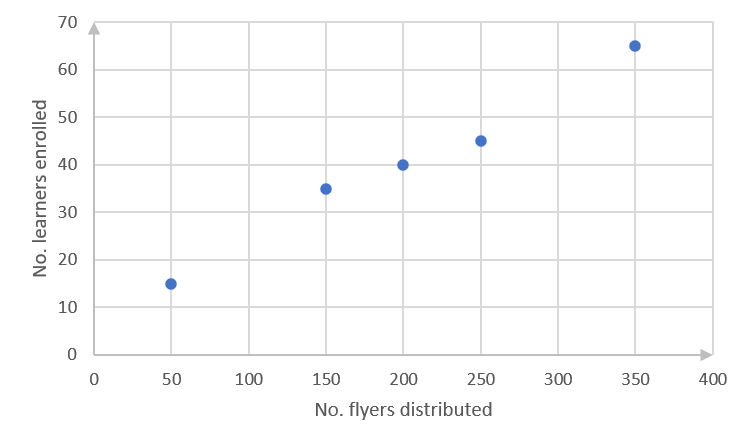
      Number of flyers distributed

      [latex]\scriptsize x[/latex]

      		 Number of learners enrolled

      [latex]\scriptsize y[/latex]

      		 [latex]\scriptsize x-\bar{x}[/latex] [latex]\scriptsize y-\bar{y}[/latex] [latex]\scriptsize (x-\bar{x})(y-\bar{y})[/latex] [latex]\scriptsize (x-\bar{x})^2[/latex]
      [latex]\scriptsize 50[/latex] [latex]\scriptsize 15[/latex] [latex]\scriptsize -150[/latex] [latex]\scriptsize -25[/latex] [latex]\scriptsize 3~750[/latex] [latex]\scriptsize 22~500[/latex]
      [latex]\scriptsize 250[/latex] [latex]\scriptsize 45[/latex] [latex]\scriptsize 50[/latex] [latex]\scriptsize 5[/latex] [latex]\scriptsize 250[/latex] [latex]\scriptsize 2~500[/latex]
      [latex]\scriptsize 200[/latex] [latex]\scriptsize 40[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize 0[/latex]
      [latex]\scriptsize 350[/latex] [latex]\scriptsize 65[/latex] [latex]\scriptsize 150[/latex] [latex]\scriptsize 25[/latex] [latex]\scriptsize 3~750[/latex] [latex]\scriptsize 22~500[/latex]
      [latex]\scriptsize 150[/latex] [latex]\scriptsize 35[/latex] [latex]\scriptsize -50[/latex] [latex]\scriptsize -5[/latex] [latex]\scriptsize 250[/latex] [latex]\scriptsize 2~500[/latex]
      Sums [latex]\scriptsize 1~000[/latex] [latex]\scriptsize 200[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize 8~000[/latex] [latex]\scriptsize 50~000[/latex]
      Mean [latex]\scriptsize 200[/latex] [latex]\scriptsize 40[/latex]

      Gradient:
      [latex]\scriptsize \begin{align*}b&=\displaystyle \frac{{\sum{{(x-\bar{x})(y-\bar{y})}}}}{{\sum{{{{{(x-\bar{x})}}^{2}}}}}}\\&=\displaystyle \frac{{8\text{ 0}00}}{{50\text{ }000}}\\&=0.16\end{align*}[/latex]
      y-intercept:
      [latex]\scriptsize \begin{align*}a&=\bar{y}-b\bar{x}\\&=40-(0.16)(200)\\&=40-32\\&=8\end{align*}[/latex]
      Regression equation: substituting for [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] in [latex]\scriptsize \hat{y}=a+bx[/latex]:
      [latex]\scriptsize \hat{y}=8+0.16x[/latex]

    3. According to the equation, the number of learners that would be enrolled if [latex]\scriptsize 500[/latex] flyers were sent out would be:
      [latex]\scriptsize \begin{align*}\hat{y}&=8+0.16x\\\hat{y}&=8+0.16(500)\\&=8+80\\&=88\end{align*}[/latex]
  3. .
    Internal examinations [latex]\scriptsize (x)[/latex] [latex]\scriptsize 80[/latex] [latex]\scriptsize 68[/latex] [latex]\scriptsize 94[/latex] [latex]\scriptsize 72[/latex] [latex]\scriptsize 74[/latex] [latex]\scriptsize 83[/latex] [latex]\scriptsize 56[/latex] [latex]\scriptsize 68[/latex] [latex]\scriptsize 65[/latex] [latex]\scriptsize 75[/latex]
    External examinations [latex]\scriptsize (x)[/latex] [latex]\scriptsize 72[/latex] [latex]\scriptsize 71[/latex] [latex]\scriptsize 96[/latex] [latex]\scriptsize 77[/latex] [latex]\scriptsize 82[/latex] [latex]\scriptsize 72[/latex] [latex]\scriptsize 58[/latex] [latex]\scriptsize 83[/latex] [latex]\scriptsize 78[/latex] [latex]\scriptsize 80[/latex]
    1. .
    2. .
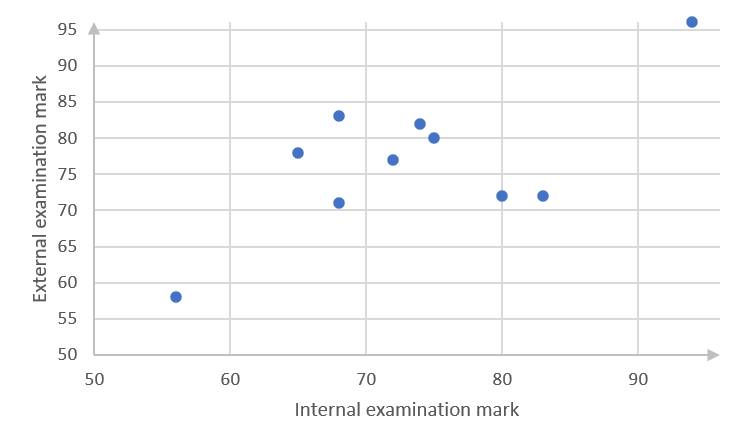
      Internal examinations [latex]\scriptsize \%[/latex]

      [latex]\scriptsize x[/latex]

      		 External examinations [latex]\scriptsize \%[/latex]

      [latex]\scriptsize y[/latex]

      		 [latex]\scriptsize x-\bar{x}[/latex] [latex]\scriptsize y-\bar{y}[/latex] [latex]\scriptsize (x-\bar{x})(y-\bar{y})[/latex] [latex]\scriptsize (x-\bar{x})^2[/latex]
      [latex]\scriptsize 80[/latex] [latex]\scriptsize 72[/latex] [latex]\scriptsize 6.5[/latex] [latex]\scriptsize -4.9[/latex] [latex]\scriptsize 31.85[/latex] [latex]\scriptsize 42.25[/latex]
      [latex]\scriptsize 68[/latex] [latex]\scriptsize 71[/latex] [latex]\scriptsize -5.5[/latex] [latex]\scriptsize -5.9[/latex] [latex]\scriptsize 32.45[/latex] [latex]\scriptsize 30.25[/latex]
      [latex]\scriptsize 94[/latex] [latex]\scriptsize 96[/latex] [latex]\scriptsize 20.5[/latex] [latex]\scriptsize 19.1[/latex] [latex]\scriptsize 391.55[/latex] [latex]\scriptsize 420.25[/latex]
      [latex]\scriptsize 72[/latex] [latex]\scriptsize 77[/latex] [latex]\scriptsize -1.5[/latex] [latex]\scriptsize 0.1[/latex] [latex]\scriptsize -0.15[/latex] [latex]\scriptsize 2.25[/latex]
      [latex]\scriptsize 74[/latex] [latex]\scriptsize 82[/latex] [latex]\scriptsize 0.5[/latex] [latex]\scriptsize 5.1[/latex] [latex]\scriptsize 2.55[/latex] [latex]\scriptsize 0.25[/latex]
      [latex]\scriptsize 83[/latex] [latex]\scriptsize 72[/latex] [latex]\scriptsize 9.5[/latex] [latex]\scriptsize -4.9[/latex] [latex]\scriptsize -46.55[/latex] [latex]\scriptsize 90.25[/latex]
      [latex]\scriptsize 56[/latex] [latex]\scriptsize 58[/latex] [latex]\scriptsize -17.5[/latex] [latex]\scriptsize -18.9[/latex] [latex]\scriptsize 330.75[/latex] [latex]\scriptsize 306.25[/latex]
      [latex]\scriptsize 68[/latex] [latex]\scriptsize 83[/latex] [latex]\scriptsize -5.5[/latex] [latex]\scriptsize 6.1[/latex] [latex]\scriptsize -33.55[/latex] [latex]\scriptsize 30.25[/latex]
      [latex]\scriptsize 65[/latex] [latex]\scriptsize 78[/latex] [latex]\scriptsize -8.5[/latex] [latex]\scriptsize 1.1[/latex] [latex]\scriptsize -9.35[/latex] [latex]\scriptsize 72.25[/latex]
      [latex]\scriptsize 75[/latex] [latex]\scriptsize 80[/latex] [latex]\scriptsize 1.5[/latex] [latex]\scriptsize 3.1[/latex] [latex]\scriptsize 4.65[/latex] [latex]\scriptsize 2.25[/latex]
      Sums [latex]\scriptsize 735[/latex] [latex]\scriptsize 769[/latex] [latex]\scriptsize 640.5[/latex] [latex]\scriptsize 996.5[/latex]
      Mean [latex]\scriptsize 73.5[/latex] [latex]\scriptsize 76.9[/latex]

      Gradient:
      [latex]\scriptsize \begin{align*}b&=\displaystyle \frac{{\sum{{(x-\bar{x})(y-\bar{y})}}}}{{\sum{{{{{(x-\bar{x})}}^{2}}}}}}\\&=\displaystyle \frac{{640.5}}{{996.5}}\\&=0.64\end{align*}[/latex]
      y-intercept:
      [latex]\scriptsize \begin{align*}a&=\bar{y}-b\bar{x}\\&=76.9-(0.64)(73.5)\\&=76.9-47.04\\&=29.86\end{align*}[/latex]
      Regression equation: substituting for [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] in [latex]\scriptsize \hat{y}=a+bx[/latex]:
      [latex]\scriptsize \hat{y}=29.86+0.64x[/latex]

    3. .
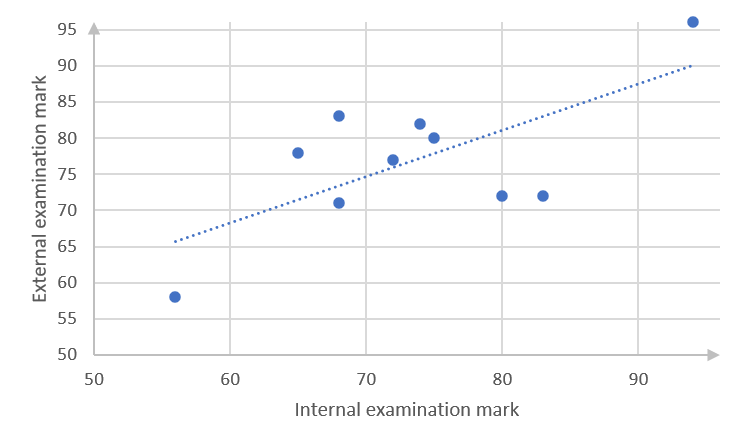
    4. The regression equation predicts that the final examination mark of a learner who scores [latex]\scriptsize 70[/latex] in the internal examination will be:
      [latex]\scriptsize \begin{align*}\hat{y}&=29.86+0.64x\\&=29.86+0.64(70)\\&=29.86+44.8\\&=74.66\end{align*}[/latex]

See question 2 in unit 2 assessment.

  1. .
    Year [latex]\scriptsize 2010[/latex] [latex]\scriptsize 2011[/latex] [latex]\scriptsize 2012[/latex] [latex]\scriptsize 2013[/latex] [latex]\scriptsize 2014[/latex] [latex]\scriptsize 2015[/latex] [latex]\scriptsize 2016[/latex] [latex]\scriptsize 2017[/latex]
    Deaths [latex]\scriptsize ('000)[/latex] [latex]\scriptsize 38.0[/latex] [latex]\scriptsize 35.8[/latex] [latex]\scriptsize 34.1[/latex] [latex]\scriptsize 32.6[/latex] [latex]\scriptsize 31.8[/latex] [latex]\scriptsize 31.5[/latex] [latex]\scriptsize 31.3[/latex] [latex]\scriptsize 29.9[/latex]
    1. .
    2. .
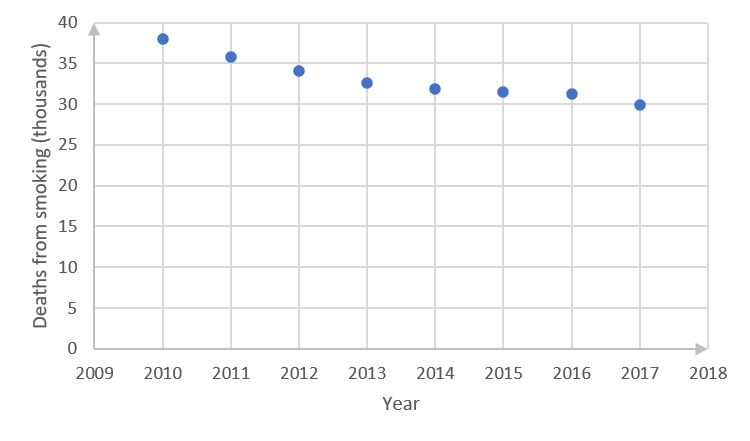
      Year

      [latex]\scriptsize x[/latex]

      		 Deaths from smoking  [latex]\scriptsize ('000)[/latex]

      [latex]\scriptsize y[/latex]

      		 [latex]\scriptsize x-\bar{x}[/latex] [latex]\scriptsize y-\bar{y}[/latex] [latex]\scriptsize (x-\bar{x})(y-\bar{y})[/latex] [latex]\scriptsize (x-\bar{x})^2[/latex]
      [latex]\scriptsize 2010[/latex] [latex]\scriptsize 38[/latex] [latex]\scriptsize -3.5[/latex] [latex]\scriptsize 4.87[/latex] [latex]\scriptsize -17.05[/latex] [latex]\scriptsize 12.25[/latex]
      [latex]\scriptsize 2011[/latex] [latex]\scriptsize 35.8[/latex] [latex]\scriptsize -2.5[/latex] [latex]\scriptsize 2.67[/latex] [latex]\scriptsize -6.68[/latex] [latex]\scriptsize 6.25[/latex]
      [latex]\scriptsize 2012[/latex] [latex]\scriptsize 34.1[/latex] [latex]\scriptsize -1.5[/latex] [latex]\scriptsize 0.97[/latex] [latex]\scriptsize -1.46[/latex] [latex]\scriptsize 2.25[/latex]
      [latex]\scriptsize 2013[/latex] [latex]\scriptsize 32.6[/latex] [latex]\scriptsize -0.5[/latex] [latex]\scriptsize -0.53[/latex] [latex]\scriptsize 0.27[/latex] [latex]\scriptsize 0.25[/latex]
      [latex]\scriptsize 2014[/latex] [latex]\scriptsize 31.8[/latex] [latex]\scriptsize 0.5[/latex] [latex]\scriptsize -1.33[/latex] [latex]\scriptsize -0.67[/latex] [latex]\scriptsize 0.25[/latex]
      [latex]\scriptsize 2015[/latex] [latex]\scriptsize 31.5[/latex] [latex]\scriptsize 1.5[/latex] [latex]\scriptsize -1.63[/latex] [latex]\scriptsize -2.45[/latex] [latex]\scriptsize 2.25[/latex]
      [latex]\scriptsize 2016[/latex] [latex]\scriptsize 31.3[/latex] [latex]\scriptsize 2.5[/latex] [latex]\scriptsize -1.83[/latex] [latex]\scriptsize -4.58[/latex] [latex]\scriptsize 6.25[/latex]
      [latex]\scriptsize 2017[/latex] [latex]\scriptsize 29.9[/latex] [latex]\scriptsize 3.5[/latex] [latex]\scriptsize -3.23[/latex] [latex]\scriptsize -11.31[/latex] [latex]\scriptsize 12.25[/latex]
      Sums [latex]\scriptsize 16~108[/latex] [latex]\scriptsize 265[/latex] [latex]\scriptsize -43.93[/latex] [latex]\scriptsize 42[/latex]
      Mean [latex]\scriptsize 2~013.5[/latex] [latex]\scriptsize 33.13[/latex]

      Gradient:
      [latex]\scriptsize \begin{align*}b&=\displaystyle \frac{{\sum{{(x-\bar{x})(y-\bar{y})}}}}{{\sum{{{{{(x-\bar{x})}}^{2}}}}}}\\&=\displaystyle \frac{{-43.93}}{{42}}\\&=-1.05\end{align*}[/latex]
      y-intercept:
      [latex]\scriptsize \begin{align*}a&=\bar{y}-b\bar{x}\\&=33.13-(-1.05)(2013.5)\\&=33.13+2114.18\\&=2147.31\end{align*}[/latex]
      Regression equation: substituting for [latex]\scriptsize b[/latex] and [latex]\scriptsize a[/latex] in [latex]\scriptsize \hat{y}=a+bx[/latex]:
      [latex]\scriptsize \hat{y}=2147.31-1.05x[/latex]

    3. .
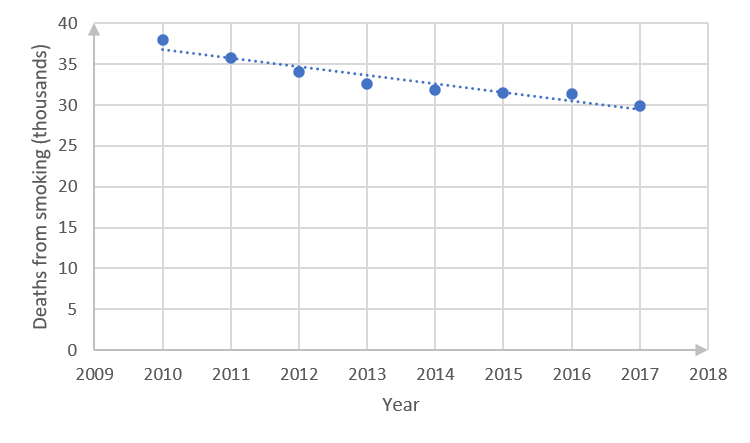
    4. The regression equation indicates that the number of deaths (thousands) from smoking predicted for [latex]\scriptsize 2022[/latex] will be:
      [latex]\scriptsize \begin{align*}\hat{y}&=2147.31-1.05x\\&=2147.31-1.05(2022)\\&=2147.31-2123.1\\&=24.21\end{align*}[/latex]

Back to Unit 3: Assessment

Media Attributions

License

Icon for the Creative Commons Attribution 4.0 International License

National Curriculum (Vocational) Mathematics Level 4 by Gill Scott is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book