Unit outcomes

By the end of this unit you will be able to:

• Find the inverse of [latex]\scriptsize y=a{{x}^{2}}[/latex].
• Sketch the inverse of [latex]\scriptsize y=a{{x}^{2}}[/latex].
• Answer questions about the domain, range, shape, continuity and other characteristics of the inverse graph.

What you should know

Before you start this unit, make sure you can:

• Determine the inverse of a function. Refer to unit 1 if you need help with this.
• Determine if a relation is a function or not using the vertical line test. Refer to unit 1 if you need help with this.
• Determine if a function is invertible or not. Refer to unit 1 if you need help with this.
• Sketch a quadratic function. Refer to level 2 subject outcome 2.1 unit 2 if you need help with this.

Introduction

We saw in the previous unit that linear functions are one-to-one functions and, therefore, are invertible – their inverses are also functions. However, is the same true for quadratic functions of the form [latex]\scriptsize y=a{{x}^{2}}[/latex]? Are quadratic functions of the form [latex]\scriptsize y=a{{x}^{2}}[/latex] invertible? Is the inverse of a quadratic function of the form [latex]\scriptsize y=a{{x}^{2}}[/latex] also a function? If not, is there a way for us to make the inverse of a quadratic function of the form [latex]\scriptsize y=a{{x}^{2}}[/latex] a function?

These are the questions we will answer in this unit.

The inverse of the quadratic function

Let’s explore the inverse of quadratic functions of the form [latex]\scriptsize y=a{{x}^{2}}[/latex].

Activity 2.1: The inverse of a quadratic function

Time required: 30 minutes

What you need:

• a blank piece of paper or graph paper
• a pen or pencil
• a ruler

What to do:

If you don’t have a piece of graph paper, start by drawing a Cartesian plane on your piece of paper. Use a scale of about [latex]\scriptsize 1\ \text{cm}[/latex] per unit.

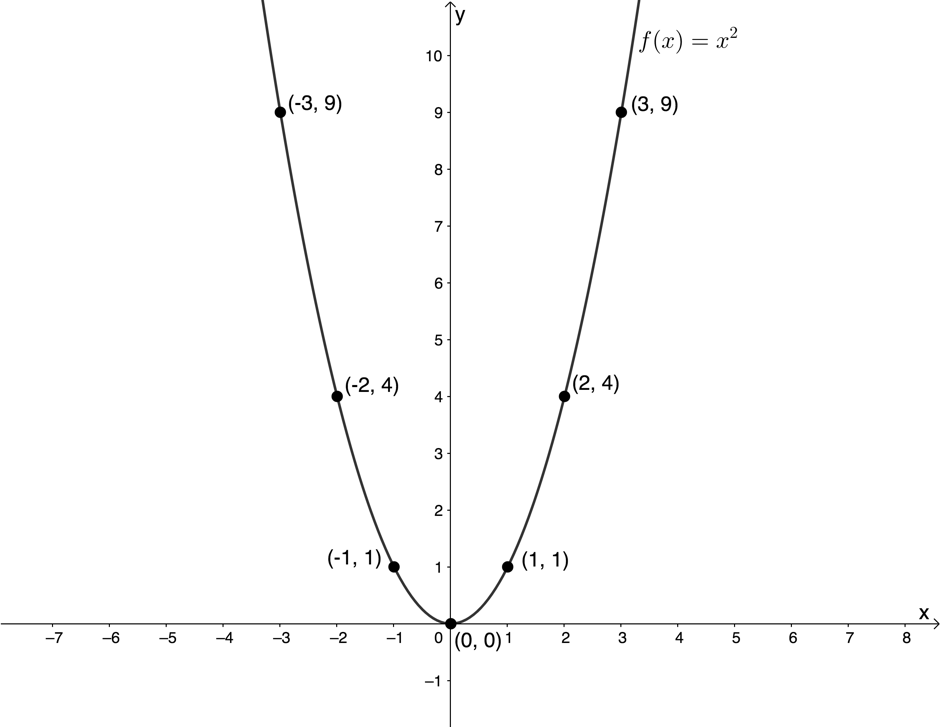
1. Plot the function [latex]\scriptsize f(x)={{x}^{2}}[/latex]. If you need to, you can create a table of values and plot point-by-point with at least five points.
2. Now, determine the inverse of [latex]\scriptsize f[/latex] in the form ‘[latex]\scriptsize y=[/latex]’.
3. Plot the inverse of [latex]\scriptsize f[/latex] on your Cartesian plane. You could do this by creating a table of values and plotting point-by-point with at least five points.
4. Is the inverse of [latex]\scriptsize f[/latex] a function? Use the vertical line test to make sure.
5. What is the domain and range of [latex]\scriptsize f[/latex] and of the inverse of [latex]\scriptsize f[/latex]?
6. About what line are the graphs of [latex]\scriptsize f[/latex] and the inverse of [latex]\scriptsize f[/latex] symmetrical?
7. What could you do to the function [latex]\scriptsize f(x)={{x}^{2}}[/latex] to make sure that its inverse was a function?

What did you find?

1. Here is a table of suitable values.
   

   [latex]\scriptsize x[/latex]	[latex]\scriptsize -3[/latex]	[latex]\scriptsize -2[/latex]	[latex]\scriptsize -1[/latex]	[latex]\scriptsize 0[/latex]	[latex]\scriptsize 1[/latex]	[latex]\scriptsize 2[/latex]	[latex]\scriptsize 3[/latex]
   [latex]\scriptsize f(x)={{x}^{2}}[/latex]	[latex]\scriptsize 9[/latex]	[latex]\scriptsize 4[/latex]	[latex]\scriptsize 1[/latex]	[latex]\scriptsize 0[/latex]	[latex]\scriptsize 1[/latex]	[latex]\scriptsize 4[/latex]	[latex]\scriptsize 9[/latex]

   .
   

2. [latex]\scriptsize y={{x}^{2}}[/latex]
   Inverse:
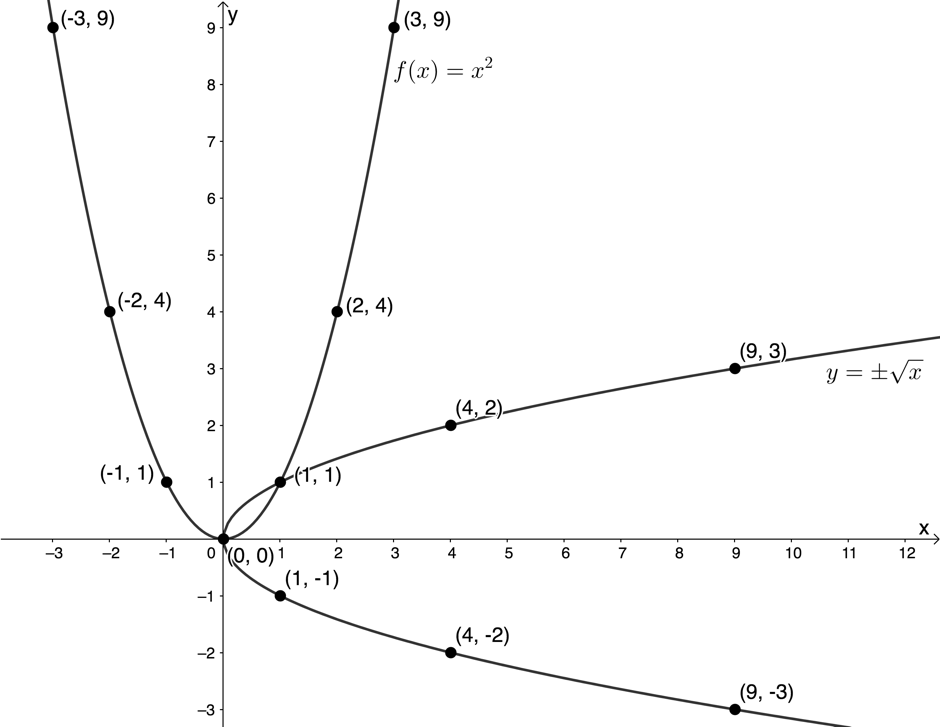
   [latex]\scriptsize \displaystyle \begin{align*}x&={{y}^{2}}\\\therefore y&=\pm \sqrt{x}\end{align*}[/latex]
3. Here is a table of suitable values.
   

   [latex]\scriptsize x[/latex]	[latex]\scriptsize 0[/latex]	[latex]\scriptsize 1[/latex]	[latex]\scriptsize 4[/latex]	[latex]\scriptsize 9[/latex]
   [latex]\scriptsize y=\pm \sqrt{x}[/latex]	[latex]\scriptsize 0[/latex]	[latex]\scriptsize \pm 1[/latex]	[latex]\scriptsize \pm 2[/latex]	[latex]\scriptsize \pm 3[/latex]

   

4. The inverse of [latex]\scriptsize f[/latex] is not a function, as demonstrated by the vertical line test.
   
5. Domain of [latex]\scriptsize f[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R}\}\text{ }[/latex]
   Range of [latex]\scriptsize f[/latex]: [latex]\scriptsize \{y|y\in \mathbb{R},y\ge 0\}\text{ }[/latex]
   Domain of inverse of [latex]\scriptsize f[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R},x\ge 0\}\text{ }[/latex]
   Range of inverse of [latex]\scriptsize f[/latex]: [latex]\scriptsize \{y|y\in \mathbb{R}\}\text{ }[/latex]
6. The graphs of [latex]\scriptsize f[/latex] and the inverse of [latex]\scriptsize f[/latex] are symmetrical about the line [latex]\scriptsize y=x[/latex].
   
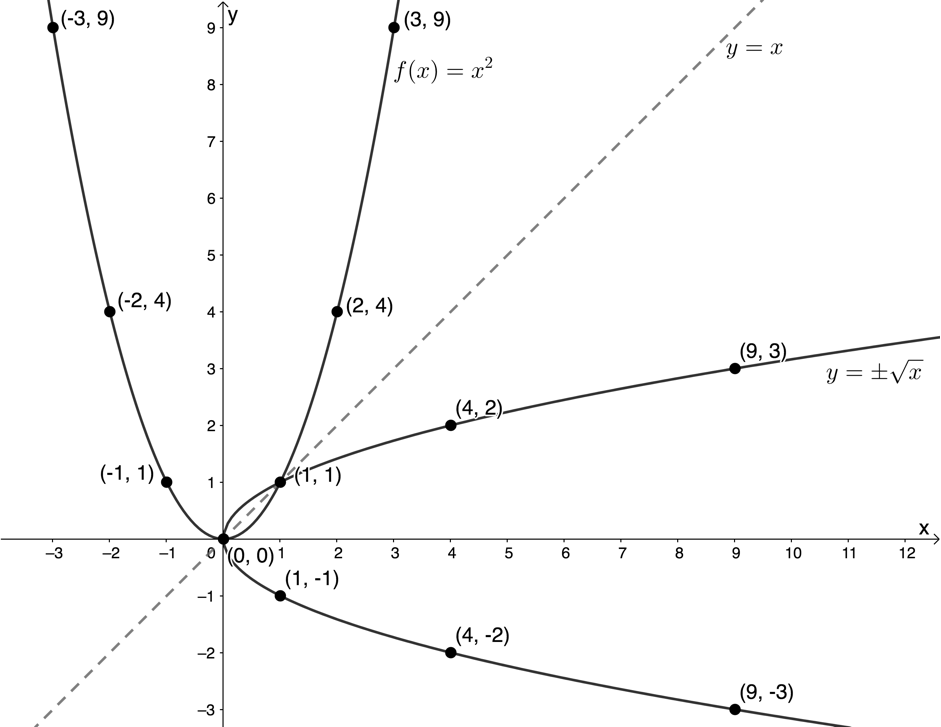
7. We can see that both the graphs of [latex]\scriptsize f[/latex] and the inverse of [latex]\scriptsize f[/latex] have two ‘arms’. It is these two ‘arms’ that mean that the inverse of [latex]\scriptsize f[/latex] is not a function. If we could remove one of the ‘arms’ of [latex]\scriptsize f[/latex], then the inverse of [latex]\scriptsize f[/latex] would also only have one ‘arm’ and would be a function.
   .
   We can remove one of the ‘arms’ of [latex]\scriptsize f[/latex] by restricting the domain. We can either restrict the domain to [latex]\scriptsize \{x|x\in \mathbb{R},x\le 0\}\text{ }[/latex] or [latex]\scriptsize \{x|x\in \mathbb{R},x\ge 0\}\text{ }[/latex].
   .
   If we restrict the domain to [latex]\scriptsize \{x|x\in \mathbb{R},x\le 0\}\text{ }[/latex], the graphs of [latex]\scriptsize f[/latex] and the inverse of [latex]\scriptsize f[/latex] are as follows. Notice that because the inverse of [latex]\scriptsize f[/latex] is now a function we can use the [latex]\scriptsize {{f}^{{-1}}}(x)[/latex] notation.
   
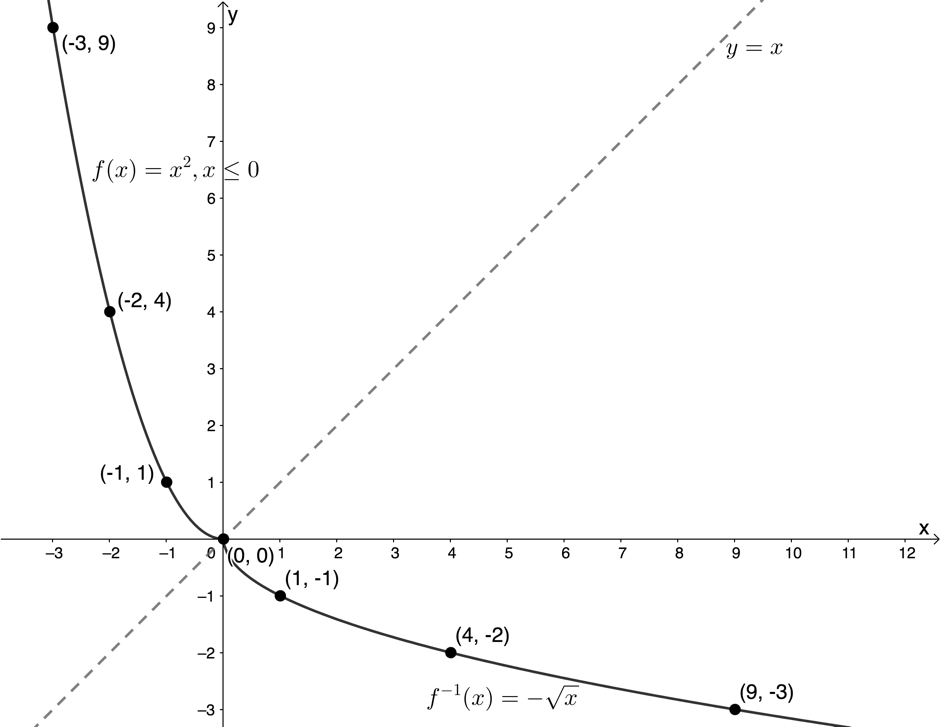
   If we restrict the domain to [latex]\scriptsize \{x|x\in \mathbb{R},x\ge 0\}\text{ }[/latex], the graphs of [latex]\scriptsize f[/latex] and the inverse of [latex]\scriptsize f[/latex] are as follows. Notice that because the inverse of [latex]\scriptsize f[/latex] is now a function we can use the [latex]\scriptsize {{f}^{{-1}}}(x)[/latex] notation.
   

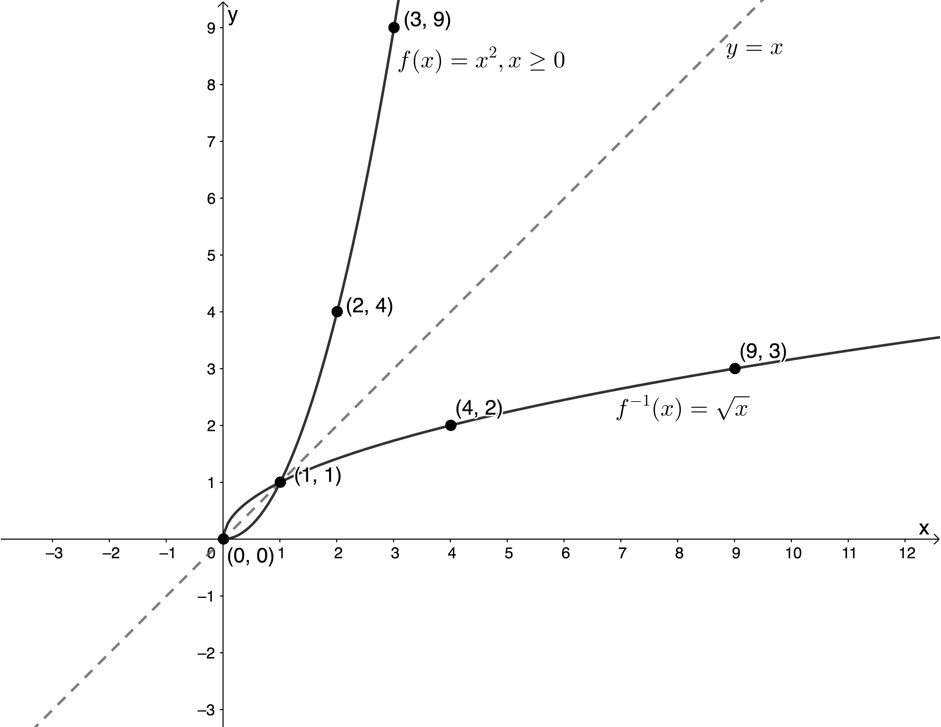
In Activity 2.1, we saw that ordinarily, the quadratic function of the form [latex]\scriptsize y=a{{x}^{2}}[/latex] is not invertible because its inverse is not also a function. However, if we restrict the domain to [latex]\scriptsize x\le 0[/latex] or [latex]\scriptsize x\ge 0[/latex], we can make the inverse a function and, hence, make the original quadratic invertible. What we are really doing when we restrict the domain like this is making the function a one-to-one function.

We also saw that, like the linear function, the quadratic function and its inverse are symmetrical about the line [latex]\scriptsize y=x[/latex]. Every point [latex]\scriptsize (x,y)[/latex] on the original function, has a corresponding symmetrical point [latex]\scriptsize (y,x)[/latex] on the inverse.

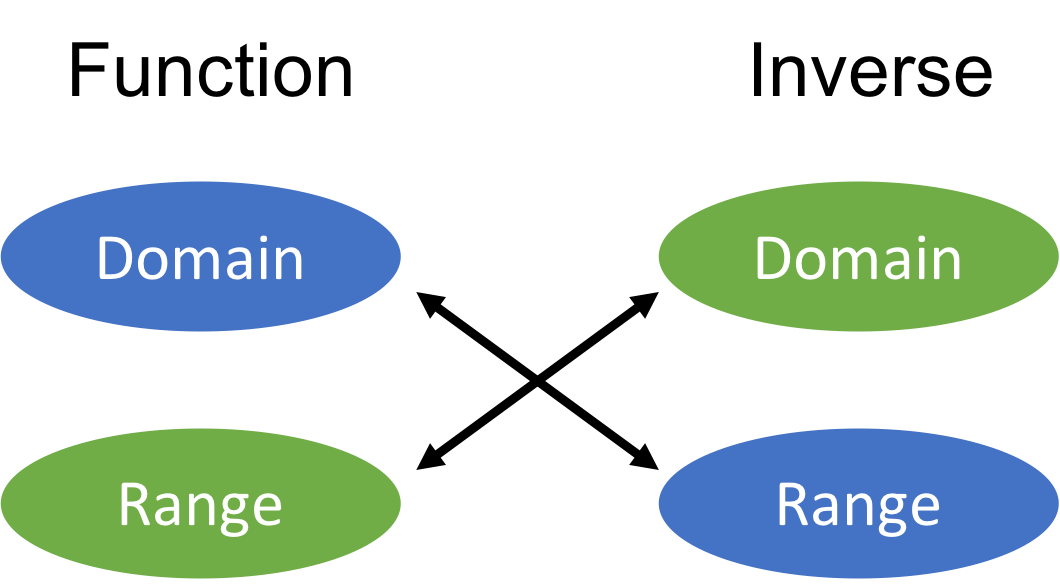
Finally, we saw that the domain of the original function becomes the range of the inverse and vice versa (see Figure 1). This remains true even when we restrict the domain of the original function. The domain of [latex]\scriptsize f(x)={{x}^{2}},x\ge 0[/latex], for example, is [latex]\scriptsize \{x|x\in \mathbb{R},x\ge 0\}\text{ }[/latex] and the range is [latex]\scriptsize \{y|y\in \mathbb{R},y\ge 0\}\text{ }[/latex]. The domain and range of the inverse of [latex]\scriptsize f(x)={{x}^{2}},x\ge 0[/latex] are [latex]\scriptsize \{x|x\in \mathbb{R},x\ge 0\}\text{ }[/latex] and [latex]\scriptsize \{y|y\in \mathbb{R},y\ge 0\}\text{ }[/latex] respectively.

Example 2.1

Given [latex]\scriptsize g(x)=3{{x}^{2}}[/latex]:

1. Determine the inverse of [latex]\scriptsize g[/latex].
2. Sketch [latex]\scriptsize g[/latex] and the inverse of [latex]\scriptsize g[/latex] on the same system of axes.
3. State the domain and range of [latex]\scriptsize g[/latex] and of the inverse of [latex]\scriptsize g[/latex].
4. Is the inverse of [latex]\scriptsize g[/latex] a function?

Solutions

1. [latex]\scriptsize g(x)=3{{x}^{2}}[/latex]. Therefore, we can write the function equation as [latex]\scriptsize y=3{{x}^{2}}[/latex]. To find the inverse, we interchange [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex].
   Inverse:
   [latex]\scriptsize \begin{align*}x & =3{{y}^{2}}\\\therefore {{y}^{2}} & =\displaystyle \frac{1}{3}x\\\therefore y & =\pm \sqrt{{\displaystyle \frac{1}{3}x}}\end{align*}[/latex]
2. .
   
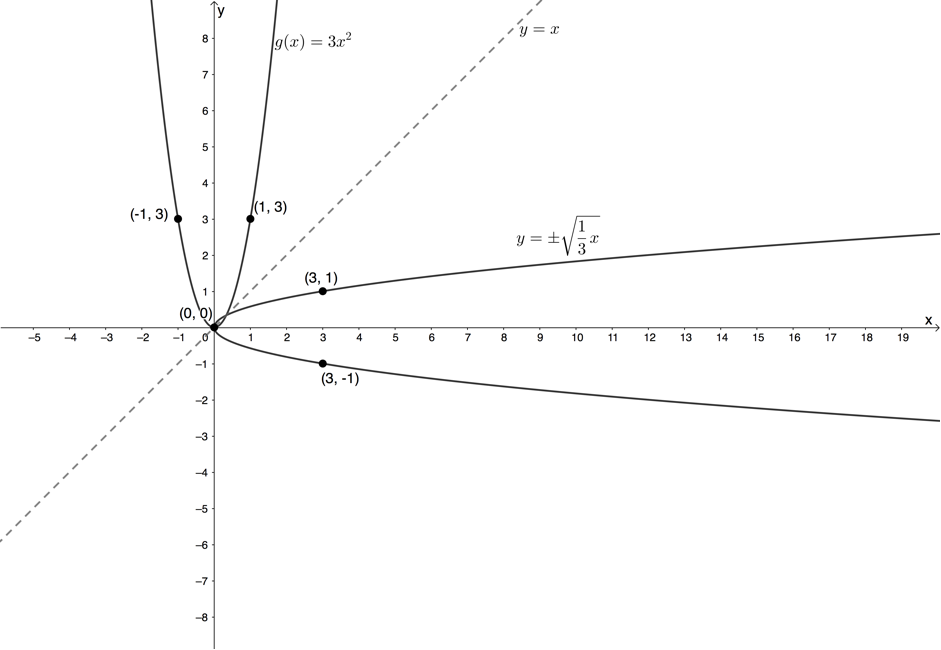
3. Domain of [latex]\scriptsize g[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R}\}\text{ }[/latex]
   Range of [latex]\scriptsize g[/latex]: [latex]\scriptsize \{y|y\in \mathbb{R},y\ge 0\}\text{ }[/latex]
   Domain of inverse of [latex]\scriptsize g[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R},x\ge 0\}\text{ }[/latex]
   Range of inverse [latex]\scriptsize g[/latex]: [latex]\scriptsize \{y|y\in \mathbb{R}\}\text{ }[/latex]
4. The inverse of [latex]\scriptsize g[/latex] is not a function. It does not pass the vertical line test. We would need to restrict the domain of [latex]\scriptsize g[/latex] in order to make its inverse a function.

Example 2.2

Given [latex]\scriptsize r(x)=-2{{x}^{2}}[/latex]:

1. State the domain and range of [latex]\scriptsize r[/latex].
2. How must the domain be restricted so that [latex]\scriptsize r[/latex] is invertible?
3. Find [latex]\scriptsize {{r}^{{-1}}}(x)[/latex].
4. State the domain and range of [latex]\scriptsize {{r}^{{-1}}}[/latex].
5. Sketch the graphs of [latex]\scriptsize r[/latex] and [latex]\scriptsize {{r}^{{-1}}}[/latex] on the same set of axes.

Solutions

1. Domain [latex]\scriptsize r[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R}\}\text{ }[/latex]
   Range of [latex]\scriptsize r[/latex]: [latex]\scriptsize \{y|y\in \mathbb{R},y\le 0\}\text{ }[/latex]
2. The domain of [latex]\scriptsize r[/latex] must be restricted to [latex]\scriptsize \{x|x\in \mathbb{R},x\le 0\}\text{ }[/latex] or [latex]\scriptsize \{x|x\in \mathbb{R},x\ge 0\}\text{ }[/latex] in order for the inverse to be a function and hence for [latex]\scriptsize r[/latex] to be invertible.
3. Option 1: Restrict the domain of [latex]\scriptsize r[/latex] to [latex]\scriptsize \{x|x\in \mathbb{R},x\le 0\}\text{ }[/latex].
   [latex]\scriptsize y=-2{{x}^{2}},x\le 0[/latex]
   Inverse:
   [latex]\scriptsize \begin{align*}x & =-2{{y}^{2}}\\\therefore 2{{y}^{2}} & =-x\\\therefore {{y}^{2}} & =-\displaystyle \frac{x}{2}\\\therefore y & =-\sqrt{{-\displaystyle \frac{x}{2}}}\\\therefore {{r}^{{-1}}} & =-\sqrt{{-\displaystyle \frac{x}{2}}}\end{align*}[/latex]
   Remember that the domain of [latex]\scriptsize r[/latex] becomes the range of [latex]\scriptsize {{r}^{{-1}}}[/latex]. The domain of [latex]\scriptsize r[/latex] was restricted to [latex]\scriptsize \{x|x\in \mathbb{R},x\le 0\}\text{ }[/latex], therefore, the range of [latex]\scriptsize {{r}^{{-1}}}[/latex] will be [latex]\scriptsize \{y|y\in \mathbb{R},y\le 0\}\text{ }[/latex]. Because the function values are restricted to [latex]\scriptsize y\le 0[/latex], we chose the negative square root.
   .
   Also note that [latex]\scriptsize \sqrt{{-\displaystyle \frac{x}{2}}}[/latex] is only defined for [latex]\scriptsize x\le 0[/latex]. However, the range of the original function [latex]\scriptsize r[/latex] is [latex]\scriptsize \{y|y\in \mathbb{R},y\le 0\}\text{ }[/latex]. The range of [latex]\scriptsize r[/latex] becomes the domain of [latex]\scriptsize {{r}^{{-1}}}[/latex]. Hence the domain of [latex]\scriptsize {{r}^{{-1}}}[/latex] is [latex]\scriptsize \{x|x\in \mathbb{R},x\le 0\}\text{ }[/latex] and so [latex]\scriptsize \sqrt{{-\displaystyle \frac{x}{2}}}[/latex] is defined.
   .
   Option 2: Restrict the domain of [latex]\scriptsize r[/latex] to [latex]\scriptsize \{x|x\in \mathbb{R},x\ge 0\}\text{ }[/latex].
   [latex]\scriptsize y=-2{{x}^{2}},x\ge 0[/latex]
   Inverse:
   [latex]\scriptsize \begin{align*}x & =-2{{y}^{2}}\\\therefore 2{{y}^{2}} & =-x\\\therefore {{y}^{2}} & =-\displaystyle \frac{x}{2}\\\therefore y & =+\sqrt{{-\displaystyle \frac{x}{2}}}\\\therefore {{r}^{{-1}}} & =+\sqrt{{-\displaystyle \frac{x}{2}}}\end{align*}[/latex]
   Remember that the domain of [latex]\scriptsize r[/latex] becomes the range of [latex]\scriptsize {{r}^{{-1}}}[/latex]. The domain of [latex]\scriptsize r[/latex] was restricted to [latex]\scriptsize \{x|x\in \mathbb{R},x\ge 0\}\text{ }[/latex], therefore, the range of [latex]\scriptsize {{r}^{{-1}}}[/latex] will be [latex]\scriptsize \{y|y\in \mathbb{R},y\ge 0\}\text{ }[/latex]. Because the function values are restricted to [latex]\scriptsize y\ge 0[/latex], we chose the positive square root.
   .
   Also note that [latex]\scriptsize \sqrt{{-\displaystyle \frac{x}{2}}}[/latex] is only defined for [latex]\scriptsize x\le 0[/latex]. However, the range of the original function [latex]\scriptsize r[/latex] is [latex]\scriptsize \{y|y\in \mathbb{R},y\le 0\}\text{ }[/latex]. The range of [latex]\scriptsize r[/latex] becomes the domain of [latex]\scriptsize {{r}^{{-1}}}[/latex]. Hence the domain of [latex]\scriptsize {{r}^{{-1}}}[/latex] is [latex]\scriptsize \{x|x\in \mathbb{R},x\le 0\}\text{ }[/latex] and so [latex]\scriptsize \sqrt{{-\displaystyle \frac{x}{2}}}[/latex] is defined.
4. Option 1:
   Domain of [latex]\scriptsize {{r}^{{-1}}}[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R},x\le 0\}\text{ }[/latex] – this was the range of [latex]\scriptsize r[/latex]
   Range of [latex]\scriptsize {{r}^{{-1}}}[/latex]: [latex]\scriptsize \{y|y\in \mathbb{R},y\le 0\}\text{ }[/latex] – this was the restricted domain of [latex]\scriptsize r[/latex]
   Option 2:
   Domain of [latex]\scriptsize {{r}^{{-1}}}[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R},x\le 0\}\text{ }[/latex] – this was the range of [latex]\scriptsize r[/latex]
   Range of [latex]\scriptsize {{r}^{{-1}}}[/latex]: [latex]\scriptsize \{y|y\in \mathbb{R},y\ge 0\}\text{ }[/latex] – this was the restricted domain of [latex]\scriptsize r[/latex]
5. Here is a sketch for option 1 where the domain [latex]\scriptsize r[/latex] is restricted to [latex]\scriptsize \{x|x\in \mathbb{R},x\le 0\}\text{ }[/latex]. It is usually easiest to plot these graphs using a table of suitable values and point-by-point plotting. Sketching the axis of symmetry (the line [latex]\scriptsize y=x[/latex]) also helps you to get the shapes of the graphs correct.
   
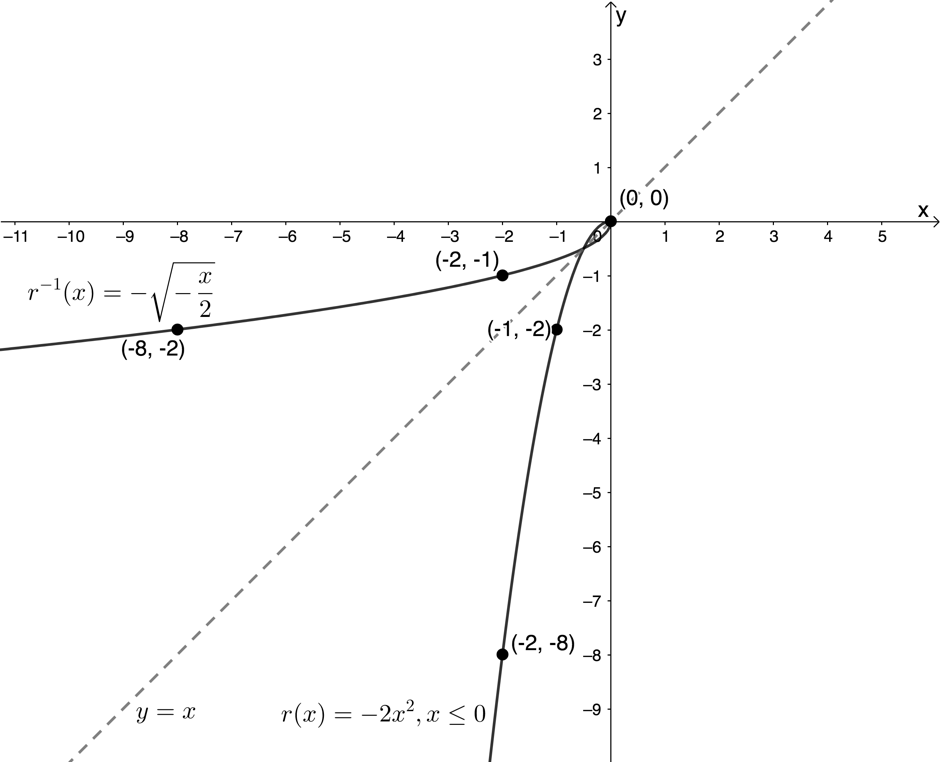
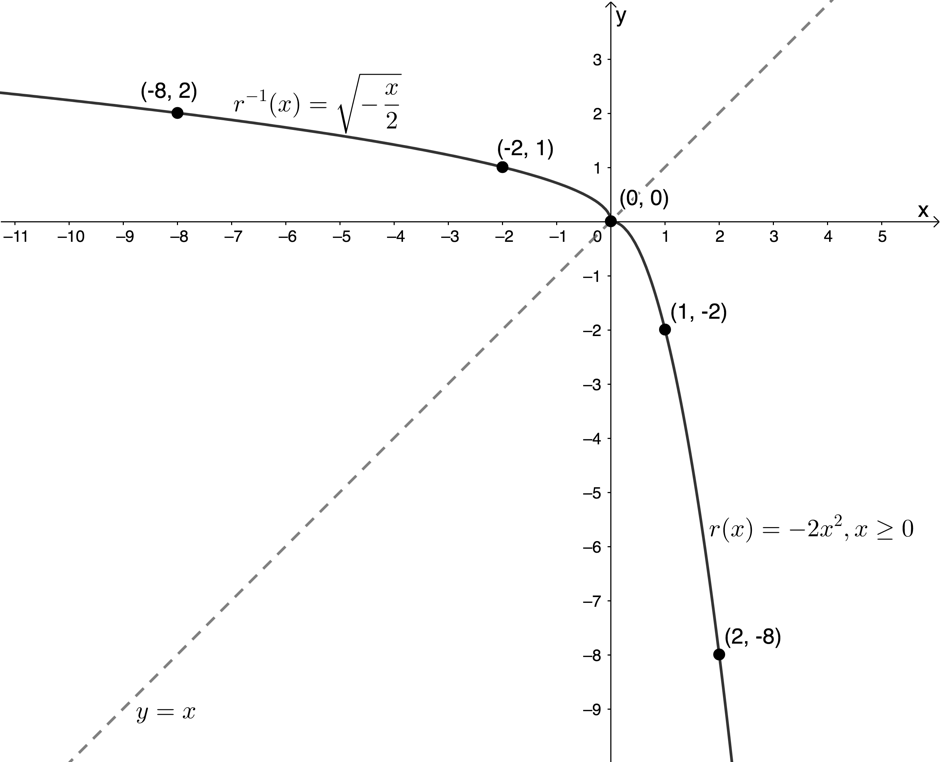
   Here is a sketch for option 2 where the domain [latex]\scriptsize r[/latex] is restricted to [latex]\scriptsize \{x|x\in \mathbb{R},x\ge 0\}\text{ }[/latex].
   

Exercise 2.1

1. Determine the inverse for each of the following, leaving your answer in ‘[latex]\scriptsize y=[/latex]’ form:
   1. [latex]\scriptsize y=\displaystyle \frac{5}{3}{{x}^{2}}[/latex]
   2. [latex]\scriptsize {{x}^{2}}+3y=0[/latex]
   3. [latex]\scriptsize 5y+10{{x}^{2}}=0[/latex]
   4. [latex]\scriptsize 2y-25=(x+4)(x-4)[/latex]
2. Given the function [latex]\scriptsize f(x)=\displaystyle \frac{1}{3}{{x}^{2}}[/latex] for [latex]\scriptsize x\le 0[/latex]:
   1. Find the inverse of [latex]\scriptsize f[/latex].
   2. State the domain and range of [latex]\scriptsize f[/latex] and the inverse of [latex]\scriptsize f[/latex].
   3. Draw [latex]\scriptsize f[/latex] and the inverse of [latex]\scriptsize f[/latex] on the same set of axes, showing at least three points on each graph.
   4. Is the inverse of [latex]\scriptsize f[/latex] a function? Explain your answer.
   5. Determine the point of intersection of [latex]\scriptsize f[/latex] and the inverse of [latex]\scriptsize f[/latex].
3. Given the graph of the parabola [latex]\scriptsize g(x)=a{{x}^{2}}[/latex] with [latex]\scriptsize x\ge 0[/latex] and passing through [latex]\scriptsize A(1,-4)[/latex]:
   
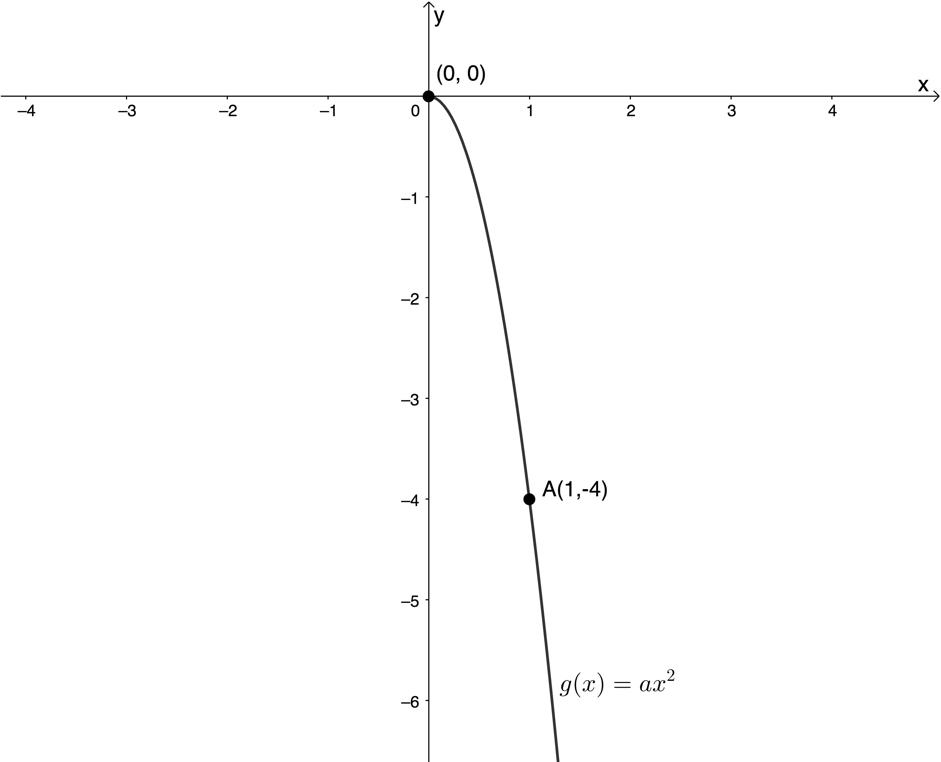
   1. Determine the equation of the parabola [latex]\scriptsize g(x)[/latex].
   2. Determine the equation of the inverse of [latex]\scriptsize g[/latex].
   3. Is the inverse of [latex]\scriptsize g[/latex] a function?
   4. Give the coordinates of the point [latex]\scriptsize B[/latex] on the inverse of [latex]\scriptsize g[/latex] and symmetrical to [latex]\scriptsize \text{A}[/latex].
   5. Determine the point of intersection of [latex]\scriptsize g[/latex] and the inverse of [latex]\scriptsize g[/latex].

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• The inverse of the quadratic function of the form [latex]\scriptsize y=a{{x}^{2}}[/latex] is not a function and therefore [latex]\scriptsize y=a{{x}^{2}}[/latex] is not invertible.
• We can make [latex]\scriptsize y=a{{x}^{2}}[/latex] invertible by restricting the domain to either [latex]\scriptsize \{x|x\le 0,x\in \mathbb{R}\}[/latex] or [latex]\scriptsize \{x|x\ge 0,x\in \mathbb{R}\}[/latex].
• The quadratic function [latex]\scriptsize y=a{{x}^{2}}[/latex] and its inverse are symmetrical about the line [latex]\scriptsize y=x[/latex].
• The domain of the quadratic function [latex]\scriptsize y=a{{x}^{2}}[/latex] becomes the range of its inverse.
• The range of the quadratic function [latex]\scriptsize y=a{{x}^{2}}[/latex] becomes the domain of its inverse.

Unit 2: Assessment

Suggested time to complete: 20 minutes

Question 1 adapted from NC(V) Mathematics Level 4 Paper 1 November 2015 question 4.4

1. Given [latex]\scriptsize f(x)={{x}^{2}}[/latex]:
   1. Draw a sketch graph of [latex]\scriptsize f[/latex], showing the coordinates of at least three points on the graph.
   2. Determine [latex]\scriptsize {{f}^{{-1}}}(x)[/latex] if the domain of [latex]\scriptsize f[/latex] is restricted to [latex]\scriptsize \{x|x\ge 0,x\in \mathbb{R}\}[/latex].
   3. Sketch the graph of [latex]\scriptsize {{f}^{{-1}}}[/latex] on the same set of axes as [latex]\scriptsize f[/latex].
   4. Determine algebraically the coordinates of the point(s) of intersection of [latex]\scriptsize f[/latex] and [latex]\scriptsize {{f}^{{-1}}}[/latex].
   5. Write down the domain of [latex]\scriptsize {{f}^{{-1}}}[/latex].

Question 2 adapted from NC(V) Mathematics Level 4 Paper 1 October 2014 question 4.4

2. Given [latex]\scriptsize f(x)=2{{x}^{2}}[/latex] for [latex]\scriptsize x\ge 0[/latex]:
   1. Determine the equation which defines the inverse of [latex]\scriptsize f[/latex] in the form ‘[latex]\scriptsize y=[/latex]’.
   2. Draw sketch graphs of [latex]\scriptsize f[/latex] and the inverse of [latex]\scriptsize f[/latex] on the same set of axes. Clearly label the graphs and indicate at least three points on each graph.
   3. Determine algebraically the intersection of the two graphs.
   4. Is the inverse of [latex]\scriptsize f[/latex] a function or a non-function? Give a reason for your answer.
   5. Write down the range of the inverse of [latex]\scriptsize f[/latex].

The full solutions are at the end of the unit.

Unit 2: Solutions

Exercise 2.1

1. .
   1. [latex]\scriptsize y=\displaystyle \frac{5}{3}{{x}^{2}}[/latex]
      Inverse:
      [latex]\scriptsize \displaystyle \begin{align*}x & =\displaystyle \frac{5}{3}{{y}^{2}}\\\therefore {{y}^{2}} & =\displaystyle \frac{3}{5}x\\\therefore y & =\pm \sqrt{{\displaystyle \frac{3}{5}x}}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}x^2+3y&=0\\ \therefore 3y&=-x^2\\ \therefore y&=-\displaystyle \frac{1}{3}x^2\end{align*}[/latex]
      Inverse:
      [latex]\scriptsize \displaystyle \begin{align*}x & =-\displaystyle \frac{1}{3}{{y}^{2}}\\\therefore {{y}^{2}} & =-3x\\\therefore y & =\pm \sqrt{{-3x}}\end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*}5y+10x^2&=0\\ \therefore 5y&=-10x^2\\ \therefore y&=-2x^2\end{align*}[/latex]
      Inverse:
      [latex]\scriptsize \displaystyle \begin{align*}x & =-2{{y}^{2}}\\\therefore {{y}^{2}} & =-\displaystyle \frac{1}{2}x\\\therefore y & =\pm \sqrt{{-\displaystyle \frac{1}{2}x}}\end{align*}[/latex]
   4. .
      [latex]\scriptsize \begin{align*}2y-25=(x+4)(x-4))\\ \therefore 2y-25=x^2-16\\ \therefore 2y=x^2+9\\ \therefore y=\displaystyle \frac{1}{2}x^2+\displaystyle \frac{9}{2}\end{align*}[/latex]
      Inverse:
      [latex]\scriptsize \displaystyle \begin{align*}x & =\displaystyle \frac{1}{2}{{y}^{2}}+\displaystyle \frac{9}{2}\\\therefore {{y}^{2}} & =2x-9\\\therefore y & =\pm \sqrt{{2x-9}}\end{align*}[/latex]
2. [latex]\scriptsize f(x)=\displaystyle \frac{1}{3}{{x}^{2}}[/latex] for [latex]\scriptsize x\le 0[/latex].
   1. [latex]\scriptsize y=\displaystyle \frac{1}{3}{{x}^{2}}[/latex]
      Inverse:
      [latex]\scriptsize \displaystyle \begin{align*}x & =\displaystyle \frac{1}{3}{{y}^{2}}\\\therefore {{y}^{2}} & =3x\\\therefore y & =-\sqrt{{3x}}\quad \text{Original domain was }x\le 0\text{ so inverse range will be }y\le 0\end{align*}[/latex]
   2. Domain of [latex]\scriptsize f[/latex]: [latex]\scriptsize \{x|x\le 0,x\in \mathbb{R}\}[/latex]
      Range of [latex]\scriptsize f[/latex]: [latex]\scriptsize \{y|y\ge 0,y\in \mathbb{R}\}[/latex]
      Domain of inverse of [latex]\scriptsize f[/latex]: [latex]\scriptsize \{x|x\ge 0,x\in \mathbb{R}\}[/latex]
      Range of inverse of [latex]\scriptsize f[/latex]: [latex]\scriptsize \{y|y\le 0,y\in \mathbb{R}\}[/latex]
   3. .
      
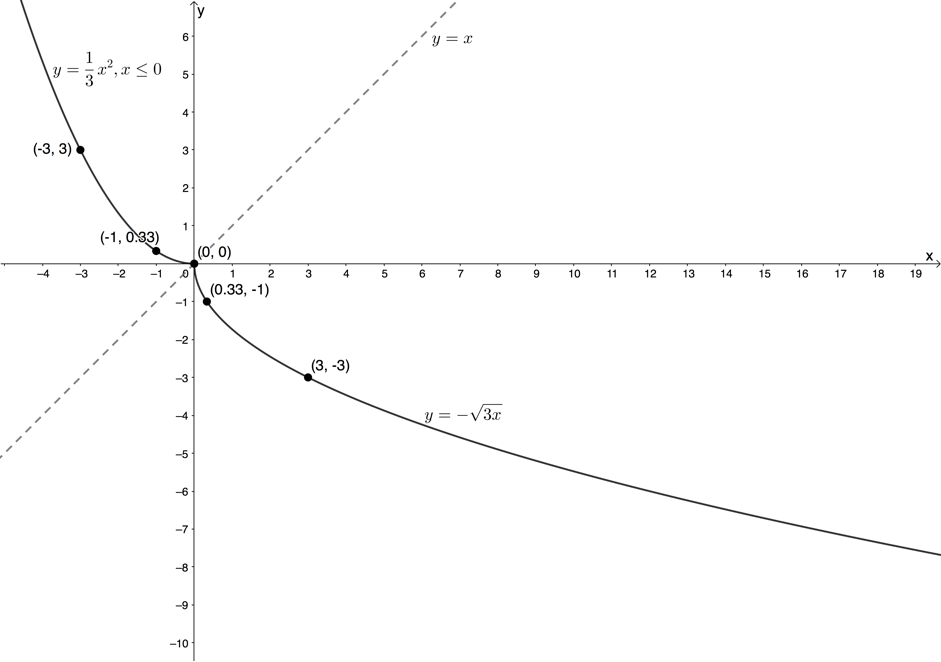
   4. The inverse of [latex]\scriptsize f[/latex] is a function as there is only ever one output value for each input value. Any vertical line will intercept the graph only once.
   5. .
      [latex]\scriptsize \begin{align*}f(x) & ={{f}^{{-1}}}(x)\\\therefore \displaystyle \frac{1}{3}{{x}^{2}} & =-\sqrt{{3x}}\\\therefore \displaystyle \frac{1}{9}{{x}^{4}} & =3x\\\therefore {{x}^{4}}-27x & =0\\\therefore x({{x}^{3}}-27) & =0\\\therefore x=0\text{ } & \text{or }{{x}^{3}}=27\\\therefore x=0\text{ } & \text{or }x=3\end{align*}[/latex]
      But the domain of [latex]\scriptsize f(x)[/latex] is restricted to [latex]\scriptsize x\le 0[/latex]. Therefore, [latex]\scriptsize x=0[/latex] is the only solution.
      [latex]\scriptsize f(0)=\displaystyle \frac{1}{3}{{(0)}^{2}}=0[/latex]. Therefore, the point of intersection is [latex]\scriptsize (0,0)[/latex].
3. .
   1. [latex]\scriptsize g(x)=a{{x}^{2}}[/latex] and passes through [latex]\scriptsize (1,-4)[/latex]. Therefore:
      [latex]\scriptsize \begin{align*}g(1) & =-4\\\therefore a{{(1)}^{2}} & =-4\\\therefore a & =-4\end{align*}[/latex]
      [latex]\scriptsize g(x)=-4{{x}^{2}}[/latex]
   2. [latex]\scriptsize y=-4{{x}^{2}}[/latex]
      Inverse:
      [latex]\scriptsize \begin{align*}x & =-4{{y}^{2}}\\\therefore {{y}^{2}} & =-\displaystyle \frac{1}{4}x\\\therefore y & =+\sqrt{{-\displaystyle \frac{1}{4}x}}\quad \text{Original domain was }x\ge 0\text{ so inverse range will be }y\ge 0\end{align*}[/latex]
   3. The inverse of [latex]\scriptsize g[/latex] is a function.
   4. [latex]\scriptsize B[/latex] symmetrical to [latex]\scriptsize A[/latex] about [latex]\scriptsize y=x[/latex]. Therefore, [latex]\scriptsize B(-4,1)[/latex].
   5. .
      [latex]\scriptsize \begin{align*}g(x) & ={{g}^{{-1}}}(x)\\\therefore -4{{x}^{2}} & =\sqrt{{-\displaystyle \frac{1}{4}x}}\\\therefore 16{{x}^{4}} & =-\displaystyle \frac{1}{4}x\\\therefore 64{{x}^{4}}+x & =0\\\therefore x(64{{x}^{3}}+1) & =0\\\therefore x=0\text{ } & \text{or }{{x}^{3}}=-\displaystyle \frac{1}{{64}}\\\therefore x=0\text{ } & \text{or }x=-\displaystyle \frac{1}{4}\end{align*}[/latex]
      But the domain of [latex]\scriptsize g(x)[/latex] is restricted to [latex]\scriptsize x\ge 0[/latex]. Therefore, [latex]\scriptsize x=0[/latex] is the only solution.
      [latex]\scriptsize g(0)=-4{{(0)}^{2}}=0[/latex]. Therefore, the point of intersection is [latex]\scriptsize (0,0)[/latex].

Back to Exercise 2.1

Unit 2: Assessment

1. [latex]\scriptsize f(x)={{x}^{2}}[/latex]
   1. .
      
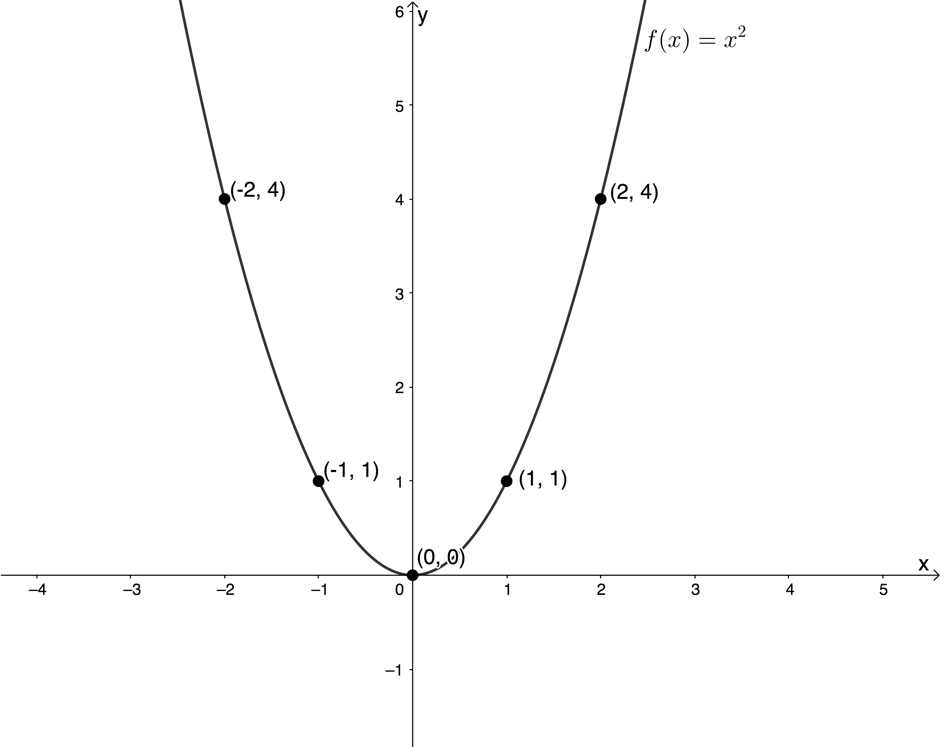
      Note that the domain was not restricted, therefore, the full parabola must be sketched.
   2. Domain of [latex]\scriptsize f[/latex] is restricted to [latex]\scriptsize \{x|x\ge 0,x\in \mathbb{R}\}[/latex]
      [latex]\scriptsize y={{x}^{2}}[/latex]
      Inverse:
      [latex]\scriptsize \displaystyle \begin{align*}x & ={{y}^{2}}\\\therefore y & =+\sqrt{x}\quad \text{Original domain was }x\ge 0\text{ so inverse range will be }y\ge 0\end{align*}[/latex]
   3. .
      
   4. .
      [latex]\scriptsize \begin{align*}f(x) & ={{f}^{{-1}}}(x)\\\therefore {{x}^{2}} & =\sqrt{x}\\\therefore {{x}^{4}} & =x\\\therefore {{x}^{4}}-x & =0\\\therefore x({{x}^{3}}-1) & =0\\\therefore x=0\text{ } & \text{or }{{x}^{3}}=1\\\therefore x=0\text{ } & \text{or }x=1\end{align*}[/latex]
      The restricted domain of [latex]\scriptsize f[/latex] allows both solutions.
      Therefore, the points of intersection are [latex]\scriptsize (0,0)[/latex] and [latex]\scriptsize (1,1)[/latex].
   5. Domain of [latex]\scriptsize {{f}^{{-1}}}[/latex]: [latex]\scriptsize \{x|x\ge 0,x\in \mathbb{R}\}[/latex]
2. Given [latex]\scriptsize f(x)=2{{x}^{2}}[/latex] for [latex]\scriptsize x\ge 0[/latex]
   1. [latex]\scriptsize f(x)=2{{x}^{2}}[/latex] or [latex]\scriptsize y=2{{x}^{2}}[/latex]
      Inverse:
      [latex]\scriptsize \begin{align*}x & =2{{y}^{2}}\\\therefore {{y}^{2}} & =\displaystyle \frac{x}{2}\\\therefore y & =+\sqrt{{\displaystyle \frac{x}{2}}}\quad \text{Domain of }f(x)\text{ is }x\ge 0,\text{ therefore, range is }y\ge 0\end{align*}[/latex]
   2. .
      
   3. .
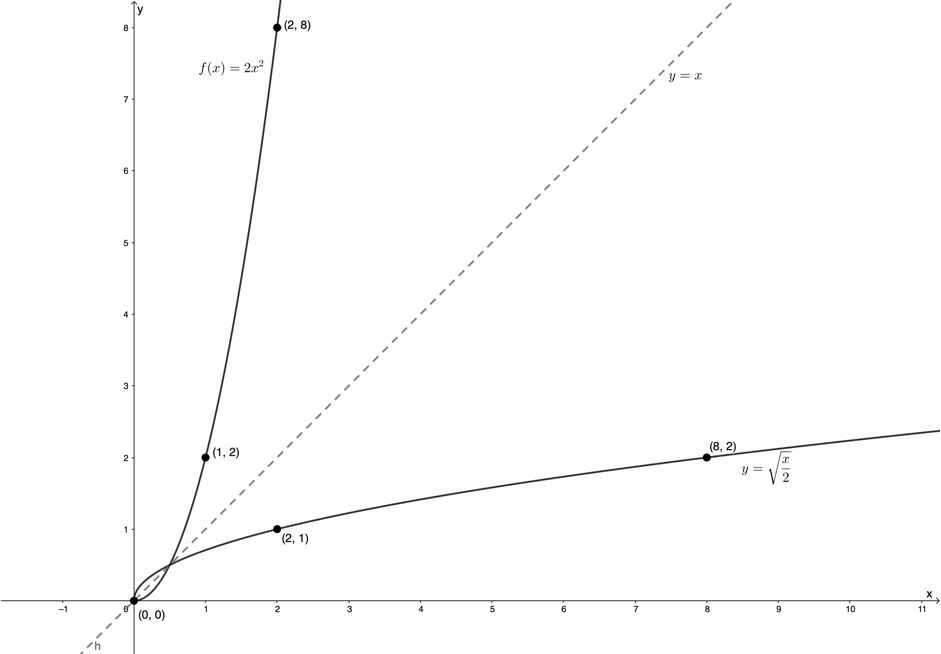
      [latex]\scriptsize \begin{align*}f(x) & ={{f}^{{-1}}}(x)\\\therefore 2{{x}^{2}} & =\sqrt{{\displaystyle \frac{x}{2}}}\\\therefore 4{{x}^{4}} & =\displaystyle \frac{x}{2}\\\therefore 8{{x}^{4}} & =x\\\therefore 8{{x}^{4}}-x & =0\\\therefore x(8{{x}^{3}}-1) & =0\\\therefore x=0\text{ } & \text{or }{{x}^{3}}=\displaystyle \frac{1}{8}\\\therefore x=0\text{ } & \text{or }x=\displaystyle \frac{1}{2}\end{align*}[/latex]
      The restricted domain of [latex]\scriptsize f[/latex] allows both solutions.
      Therefore, the points of intersection are [latex]\scriptsize (0,0)[/latex] and [latex]\scriptsize (1,\displaystyle \frac{1}{2})[/latex].
   4. The inverse of [latex]\scriptsize f[/latex] is a function. Each input value is associated with one and only one output value.
   5. Range of [latex]\scriptsize {{f}^{{-1}}}[/latex]: [latex]\scriptsize \{y|y\ge 0,y\in \mathbb{R}\}[/latex]

Back to Unit 2: Assessment