Unit outcomes

By the end of this unit you will be able to:

• Add complex numbers in standard form.
• Subtract complex numbers in standard form.
• Multiply complex numbers in standard form.
• Divide complex numbers in standard form through the use of a suitable conjugate.

What you should know

Before you start this unit, make sure you can:

• Define complex numbers. Refer to level 3 subject outcome 1.1 unit 1 if you need help with this.
• Represent complex numbers in standard rectangular coordinate form. Refer to level 3 subject outcome 1.1 unit 1 if you need help with this.
• Perform basic operations on imaginary numbers. Refer to level 3 subject outcome 1.1 unit 1 if you need help with this.
• Perform addition, subtraction and multiplication on complex numbers in standard/rectangular form. Refer to level 3 subject outcome 1.2 unit 1 if you need help with this.
• Perform division on complex numbers in standard form introducing the concept of conjugate. Refer to level 3 subject outcome 1.2 unit 1 if you need help with this.

Introduction

This subject outcome and this unit revise and build on the work you did on complex numbers in level 3 subject outcomes 1.1 and 1.2. It is important that you complete these subject outcomes before continuing.

By this stage, you should recognise the different types of numbers, as shown in Figure 1. It shows the classification of all the different kinds of real numbers beginning with the counting or natural numbers, expanding these to include zero (the whole numbers), the negative counting numbers (the integers), the fractions (rational numbers), and finally, those numbers that cannot be written as fractions (the irrational numbers).

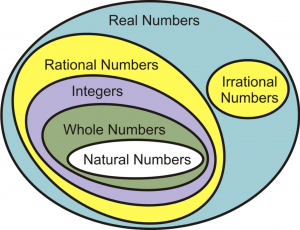
But you know that this is not the whole story. There is an even bigger set of numbers that includes the so-called imaginary numbers. This set is called the complex numbers (see Figure 2). As far as we know, the complex numbers do include everything.

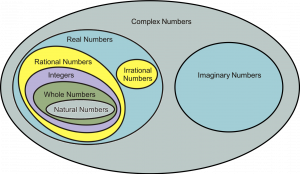
The name ‘imaginary numbers’ is actually quite unfortunate because these numbers crop up in all sorts of very ‘real’ places, from electricity to bridge-building, from car design to the flow of liquids.

When it comes to working with complex numbers (adding, subtracting, multiplying and dividing them), the good news is that all of the rules we have learnt about adding, subtracting, multiplying and dividing real numbers work in much the same way. We don’t need to learn a whole new set of mathematical techniques.

Imaginary numbers

In level 3 subject outcome 1.1 unit 1, we learnt about imaginary numbers and that the imaginary number [latex]\scriptsize i[/latex] is defined as [latex]\scriptsize \sqrt{{-1}}[/latex]. In other words, [latex]\scriptsize \sqrt{{-1}}=i[/latex]. This means that [latex]\scriptsize {{i}^{2}}={{\left( {\sqrt{{-1}}} \right)}^{2}}=-1[/latex].

This definition allows us to determine the value of numbers like [latex]\scriptsize \sqrt{{-49}}[/latex].
[latex]\scriptsize \begin{align*}\sqrt{{-49}}&=\sqrt{{49\times (-1)}}\\&=\sqrt{{49}}\times \sqrt{{-1}}\\&=7i\end{align*}[/latex]

We say that [latex]\scriptsize 7i[/latex] is an imaginary number.

Exercise 1.1

Write the following negative roots as multiples of [latex]\scriptsize i[/latex]:

1. [latex]\scriptsize \sqrt{{-25}}[/latex]
2. [latex]\scriptsize \sqrt{{-2}}[/latex]
3. [latex]\scriptsize \sqrt{{-12}}[/latex]
4. [latex]\scriptsize \sqrt{{-400}}[/latex]
5. [latex]\scriptsize \sqrt{{-24}}[/latex]

The full solutions are at the end of the unit.

What do you think happens when we square an imaginary number? Try it by working through some examples.

Example 1.1

Simplify [latex]\scriptsize {{(8i)}^{2}}[/latex].

Solution

[latex]\scriptsize \begin{align*}{{(8i)}^{2}}&=8i\times 8i\\&=8\times 8\times i\times i\\&=64\times {{i}^{2}}\end{align*}[/latex]
But [latex]\scriptsize {{i}^{2}}=-1[/latex]. Therefore, [latex]\scriptsize 64\times {{i}^{2}}=64\times (-1)=-64[/latex].

Example 1.2

Simplify [latex]\scriptsize \displaystyle \frac{{4{{i}^{3}}\times 3{{i}^{2}}}}{{6{{i}^{4}}}}[/latex].

Solution

[latex]\scriptsize \begin{align*}\displaystyle \frac{{4{{i}^{3}}\times 3{{i}^{2}}}}{{6{{i}^{4}}}}&=\displaystyle \frac{{4\times 3\times {{i}^{3}}\times {{i}^{2}}}}{{6\times {{i}^{4}}}}&& \text{We can use exponent laws: }{{i}^{3}}\times {{i}^{2}}=i\times i\times i\times i\times i={{i}^{{3+2}}}={{i}^{5}}\\&=\displaystyle \frac{{12\times {{i}^{5}}}}{{6{{i}^{4}}}}&& \text{We can use exponent laws: }\displaystyle \frac{{{{i}^{5}}}}{{{{i}^{4}}}}=\displaystyle \frac{{i\times i\times i\times i\times i}}{{i\times i\times i\times i}}={{i}^{{5-4}}}=i\\&=2i\end{align*}[/latex]

Exercise 1.2

Simplify the following:

1. [latex]\scriptsize {{(9i)}^{2}}[/latex]
2. [latex]\scriptsize {{\left( {\sqrt{{12}}i} \right)}^{2}}[/latex]
3. [latex]\scriptsize {{\left( {3\sqrt{3}i} \right)}^{2}}[/latex]
4. [latex]\scriptsize {{\left( {4i} \right)}^{3}}[/latex]
5. [latex]\scriptsize {{\left( {2\sqrt{3}i} \right)}^{3}}[/latex]
6. [latex]\scriptsize {{\left( {2\sqrt[3]{2}i} \right)}^{4}}[/latex]
7. [latex]\scriptsize \displaystyle \frac{{7{{i}^{3}}.3{{i}^{8}}.2{{i}^{5}}}}{{21{{i}^{5}}.3{{i}^{5}}}}[/latex]
8. [latex]\scriptsize \displaystyle \frac{{\sqrt{{12}}{{i}^{2}}.(-4i).3{{i}^{5}}}}{{\sqrt{{-24}}.6{{i}^{4}}}}[/latex]

The full solutions are at the end of the unit.

Complex numbers

A complex number is simply the sum of a real number and an imaginary number. Therefore, it has two parts to it – a real part and an imaginary part. Figure 3 shows an example of a complex number.

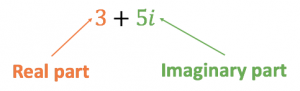
Take note!

A complex number is a number of the form [latex]\scriptsize a+bi[/latex] where:

• [latex]\scriptsize a[/latex] is the real part of the complex number
• [latex]\scriptsize bi[/latex] is the imaginary part of the complex number.

If [latex]\scriptsize b=0[/latex] , then [latex]\scriptsize a+bi[/latex] becomes just [latex]\scriptsize a[/latex] and the number is a pure real number.

If [latex]\scriptsize a=0[/latex] and [latex]\scriptsize b\ne 0[/latex], then [latex]\scriptsize a+bi[/latex] becomes just [latex]\scriptsize bi[/latex] and the number is a pure imaginary number.

Complex numbers written in the form [latex]\scriptsize a+bi[/latex] are said to be written in standard form.

We can convert complex numbers from root form to standard form and back again by remembering that [latex]\scriptsize i=\sqrt{{-1}}[/latex] and that [latex]\scriptsize {{i}^{2}}=-1[/latex].

Example 1.3

Write [latex]\scriptsize 5+\sqrt{{-3}}[/latex] in standard form.

Solution

[latex]\scriptsize \begin{align*}5+\sqrt{{-3}}&=5+\sqrt{{3\times (-1)}}\\&=5+\sqrt{3}\times \sqrt{{-1}}\\&=5+\sqrt{3}i\end{align*}[/latex]

Example 1.4

Write [latex]\scriptsize 7-7i[/latex] in root form.

Solution

[latex]\scriptsize \begin{align*}7-7i&=7-\sqrt{{49}}\cdot \sqrt{{-1}}\\&=7-\sqrt{{49\cdot (-1)}}\\&=7-\sqrt{{-49}}\end{align*}[/latex]

Some people refer to think of imaginary numbers as non-real numbers to set them apart from the real numbers, but imaginary numbers are actually very real. The name ‘imaginary numbers’ is quite an unfortunate mistake of history.

Add and subtract complex numbers

Adding and subtracting complex numbers is actually pretty simple. The basic rule is that we have to add or subtract the real parts and then add or subtract the imaginary parts. Have a look at the next example.

Example 1.5

Simplify [latex]\scriptsize (3-4i)+(2+5i)[/latex].

Solution

[latex]\scriptsize \begin{align*}(3-4i)+(2+5i)&=3-4i+2+5i\\&=3+2-4i+5i\\&=(3+2)+(-4+5)i\\&=5+i\end{align*}[/latex]

Note that all our standard expansion rules apply, for example [latex]\scriptsize -(5+4i)=-5-4i[/latex].

Example 1.6

Simplify [latex]\scriptsize (-5+2i)-(-11+7i)[/latex].

Solution

[latex]\scriptsize \begin{align*}(-5+2i)-(-11+7i)&=-5+2i+11-7i\\&=-5+11+2i-7i\\&=(-5+11)+(2i-7i)\\&=6-5i\end{align*}[/latex]

Exercise 1.3

Add or subtract the following complex numbers:

1. [latex]\scriptsize (-2-4i)+(1+6i)[/latex]
2. [latex]\scriptsize (-5+3i)-(6-i)[/latex]
3. [latex]\scriptsize (2-3i)-(3+2i)[/latex]
4. [latex]\scriptsize (-4+4i)-(-6+9i)[/latex]
5. [latex]\scriptsize (5+4i)-(3+2i)-(8-7i)[/latex]
6. [latex]\scriptsize \sqrt{{-12}}+\sqrt{{-27}}[/latex]
7. [latex]\scriptsize \sqrt{{-32}}-\sqrt{{-48}}[/latex]

The full solutions are at the end of the unit.

Multiply complex numbers

Multiplying complex numbers is very similar to expanding binomials (see Figure 4). The only difference is that we work with the real and imaginary parts separately just like we do when adding and subtracting complex numbers.

Example 1.7

Simplify [latex]\scriptsize (3+2i)(6+3i)[/latex].

Solution

[latex]\scriptsize \begin{align*}(3+2i)(6+3i)&=(3\times 6)+(3\times 3i)+(2i\times 6)+(2i\times 3i)\\&=18+9i+12i+6{{i}^{2}}&& \text{Remember }{{i}^{2}}=-1\\&=18+9i+12i+6(-1)\\&=(18-6)+(9+12)i\\&=12+21i\end{align*}[/latex]

Example 1.8

Simplify [latex]\scriptsize (4+3i)(2-5i)[/latex].

Solution

[latex]\scriptsize \begin{align*}(4+3i)(2-5i)&=(4\times 2)+\left( {4\times (-5i)} \right)+(3i\times 2)+\left( {3i\times (-5i)} \right)\\&=8-20i+6i-15{{i}^{2}}&& \text{Remember }{{i}^{2}}=-1\\&=8-20i+6i+15\\&=(8+15)+(-20+6)i\\&=23-14i\end{align*}[/latex]

Exercise 1.4

Simplify the following:

1. [latex]\scriptsize (3-4i)(2+3i)[/latex]
2. [latex]\scriptsize (2+3i)(4-i)[/latex]
3. [latex]\scriptsize (-1+2i)(-2+3i)[/latex]
4. [latex]\scriptsize {{(4+3i)}^{2}}[/latex]
5. [latex]\scriptsize (3+4i)(3-4i)[/latex]
   What kind of expression does this remind you of?
6. [latex]\scriptsize \left( {3-\sqrt{{-12}}} \right)\left( {5+\sqrt{{-27}}} \right)[/latex]

The full solutions are at the end of the unit.

Divide complex numbers

Dividing complex numbers is the most challenging of the complex number operations. However, it is still reasonably simple, so long as you know what a conjugate is. We first came across conjugates when simplifying algebraic expressions with binomial denominators.

Have a look at question 5 in Exercise 1.4 again. We were asked to multiply [latex]\scriptsize (3+4i)(3-4i)[/latex]
and found that the answer was a real number. There was no imaginary part. We call [latex]\scriptsize (3-4i)[/latex]
the complex conjugate of [latex]\scriptsize (3+4i)[/latex].

A complex conjugate is the complex number that we need to multiply another complex number by to get rid of the imaginary part. The complex conjugate of [latex]\scriptsize (a+bi)[/latex] is [latex]\scriptsize (a-bi)[/latex].

Therefore, finding complex conjugates is easy. You just need to change the sign in the complex number. The complex conjugate of [latex]\scriptsize (4-i)[/latex] is [latex]\scriptsize (4+i)[/latex]. Quickly multiply these two complex numbers together to make sure that the answer is a pure real number. Did you get [latex]\scriptsize 17[/latex]?

When you divide by a complex number, you need to multiply it by its complex conjugate. However, to keep the value of the fraction the same, you must multiply the numerator by the same complex conjugate as well.

Example 1.9

Simplify [latex]\scriptsize \displaystyle \frac{{2+5i}}{{4-i}}[/latex].

Solution

We are dividing by a complex number. Therefore, we need to multiply the denominator by its complex conjugate [latex]\scriptsize (4+i)[/latex]. However, to keep the value of the fraction the same we need to multiply the numerator by the same complex conjugate. We will, therefore, multiply the fraction by [latex]\scriptsize \displaystyle \frac{{(4+i)}}{{(4+i)}}=1[/latex].

[latex]\scriptsize \begin{align*}\displaystyle \frac{{2+5i}}{{4-i}}&=\displaystyle \frac{{(2+5i)}}{{(4-i)}}\times \displaystyle \frac{{(4+i)}}{{(4+i)}}\\&=\displaystyle \frac{{8+2i+20i+5{{i}^{2}}}}{{16+4i-4i-{{i}^{2}}}}\quad \text{Remember that }{{i}^{2}}=-1\\&=\displaystyle \frac{{8+22i-5}}{{16+1}}\\&=\displaystyle \frac{{3+22i}}{{17}}\end{align*}[/latex]

The final step is to write the answer in standard [latex]\scriptsize a+bi[/latex] form.

[latex]\scriptsize \displaystyle \frac{{3+22i}}{{17}}=\displaystyle \frac{3}{{17}}+\displaystyle \frac{{22}}{{17}}i[/latex]

Example 1.10

Simplify [latex]\scriptsize \displaystyle \frac{{2+5i}}{{5-2i}}[/latex].

Solution

The complex conjugate of [latex]\scriptsize (5-2i)[/latex] is [latex]\scriptsize (5+2i)[/latex].

[latex]\scriptsize \begin{align*}\displaystyle \frac{{2+5i}}{{5-2i}}&=\displaystyle \frac{{(2+5i)}}{{(5-2i)}}\times \displaystyle \frac{{(5+2i)}}{{(5+2i)}}\\&=\displaystyle \frac{{10+4i+25i+10{{i}^{2}}}}{{25-4{{i}^{2}}}}\\&=\displaystyle \frac{{10+29i-10}}{{25+4}}\\&=\displaystyle \frac{{29i}}{{29}}\\&=i\end{align*}[/latex]

Exercise 1.5

Simplify the following, leaving your answer in standard form:

1. [latex]\scriptsize \displaystyle \frac{3}{{5+2i}}[/latex]
2. [latex]\scriptsize \displaystyle \frac{{5+3i}}{{4i}}[/latex]
3. [latex]\scriptsize \displaystyle \frac{{3+4i}}{{2-i}}[/latex]
4. [latex]\scriptsize \displaystyle \frac{{2+\sqrt{{-12}}}}{{\sqrt{{-5}}}}[/latex]
5. [latex]\scriptsize \displaystyle \frac{{-\sqrt{{-4}}-4\sqrt{{-25}}}}{{5+i}}[/latex]
6. [latex]\scriptsize \displaystyle \frac{{(1+3i)(2-4i)}}{{1+2i}}[/latex]
7. [latex]\scriptsize \displaystyle \frac{{4+i}}{i}+\displaystyle \frac{{3-4i}}{{1-i}}[/latex]

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• What an imaginary number is.
• How to add, subtract, multiply and divide imaginary numbers.
• What a complex number is.
• How to add, subtract and multiply complex numbers.
• How to divide complex numbers using a complex conjugate.

Unit 1: Assessment

Suggested time to complete: 45 minutes

Simplify the following expressions, leaving your answer in standard form:

1. [latex]\scriptsize (3-4i)+(2+5i)[/latex]
2. [latex]\scriptsize \left( {5-\sqrt{{-50}}} \right)-\left( {3-\sqrt{{-8}}} \right)[/latex]
3. [latex]\scriptsize \left( {5-\sqrt{{-50}}} \right)\left( {3-\sqrt{{-8}}} \right)[/latex]
4. [latex]\scriptsize (-5+7i)-(-11+2i)+{{(-3-6i)}^{2}}[/latex]
5. [latex]\scriptsize {{(-3-5i)}^{2}}\cdot 6i[/latex]
6. [latex]\scriptsize \displaystyle \frac{{4-8i}}{{3-\sqrt{3}i}}[/latex]
7. [latex]\scriptsize {{(2+i)}^{2}}-{{(3-i)}^{2}}[/latex]
8. [latex]\scriptsize {{\left( {-1+\sqrt{{-3}}} \right)}^{2}}[/latex]
9. [latex]\scriptsize {{i}^{2}}(2+7i)+i(3-6i)-16-i[/latex]
10. [latex]\scriptsize \displaystyle \frac{{3-2i}}{{1+i}}-\displaystyle \frac{{1-3i}}{{1-i}}[/latex]

The full solutions are at the end of the unit.

Unit 1: Solutions

Exercise 1.1

1. [latex]\scriptsize \sqrt{{-25}}=\sqrt{{25\times (-1)}}=\sqrt{{25}}\times \sqrt{{-1}}=5i[/latex]
2. [latex]\scriptsize \sqrt{{-2}}=\sqrt{{2\times (-1)}}=\sqrt{2}\times \sqrt{{-1}}=\sqrt{2}i[/latex]
3. [latex]\scriptsize \sqrt{{-12}}=\sqrt{{12\times (-1)}}=\sqrt{{12}}\times \sqrt{{-1}}=\sqrt{{12}}i=2\sqrt{3}i[/latex]
4. [latex]\scriptsize \sqrt{{-400}}=\sqrt{{400\times (-1)}}=\sqrt{{400}}\times \sqrt{{-1}}=20i[/latex]
5. [latex]\scriptsize \sqrt{{-24}}=\sqrt{{24\times (-1)}}=\sqrt{{24}}\times \sqrt{{-1}}=2\sqrt{6}i[/latex]

Back to Exercise 1.1

Exercise 1.2

1. .
   [latex]\scriptsize \begin{align*}{{(9i)}^{2}}&=81{{i}^{2}}\\&=81\times (-1)\\&=-81\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}{{\left( {\sqrt{{12}}i} \right)}^{2}}&=12{{i}^{2}}\\&=12\times (-1)\\&=-12\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*}{{\left( {3\sqrt{3}i} \right)}^{2}}&=9\cdot 3\cdot {{i}^{2}}\\&=27{{i}^{2}}\\&=27\cdot (-1)\\&=-27\end{align*}[/latex]
4. .
   [latex]\scriptsize \begin{align*}{{\left( {4i} \right)}^{3}}&=64\cdot {{i}^{3}}\\&=64\cdot {{i}^{2}}\cdot i\\&=-64i\end{align*}[/latex]
5. .
   [latex]\scriptsize \begin{align*}{{\left( {2\sqrt{3}i} \right)}^{3}}&=8\cdot 9\sqrt{3}\cdot {{i}^{3}}\\&=72\sqrt{3}\cdot {{i}^{2}}\cdot i\\&=-72\sqrt{3}i\end{align*}[/latex]
6. .
   [latex]\scriptsize \begin{align*}{{\left( {2\sqrt[3]{2}i} \right)}^{4}}&={{2}^{4}}\cdot {{\left( {\sqrt[3]{2}} \right)}^{4}}\cdot {{i}^{4}}\\&={{2}^{4}}\cdot {{2}^{{\displaystyle \frac{4}{3}}}}\cdot {{i}^{2}}\cdot {{i}^{2}}\quad \left[ {{{i}^{2}}\times {{i}^{2}}=(-1)\times (-1)=1} \right]\\&={{2}^{{4+\displaystyle \frac{4}{3}}}}\\&={{2}^{{\displaystyle \frac{{16}}{3}}}}\end{align*}[/latex]
7. .
   [latex]\scriptsize \begin{align*}\displaystyle \frac{{7{{i}^{3}}.3{{i}^{8}}.2{{i}^{5}}}}{{21{{i}^{5}}.3{{i}^{5}}}}&=\displaystyle \frac{{42{{i}^{{16}}}}}{{63{{i}^{{10}}}}}\\&=\displaystyle \frac{{2{{i}^{4}}}}{3}\quad \left[ {{{i}^{2}}\times {{i}^{2}}=(-1)\times (-1)=1} \right]\\&=\displaystyle \frac{2}{3}\end{align*}[/latex]
8. .
   [latex]\scriptsize \begin{align*}\displaystyle \frac{{\sqrt{{12}}{{i}^{2}}\cdot (-4i)\cdot 3{{i}^{5}}}}{{\sqrt{{-24}}\cdot 6{{i}^{4}}}}&=\displaystyle \frac{{2\sqrt{3}{{i}^{2}}\cdot (-12{{i}^{6}})}}{{\sqrt{{24}}i\cdot 6{{i}^{4}}}}\\&=\displaystyle \frac{{-24\sqrt{3}{{i}^{8}}}}{{12\sqrt{6}{{i}^{5}}}}\\&=\displaystyle \frac{{-2\sqrt{3}{{i}^{3}}}}{{\sqrt{2}\sqrt{3}}}\\&=\displaystyle \frac{{2i}}{{\sqrt{2}}}\quad \text{Multiply by }\displaystyle \frac{{\sqrt{2}}}{{\sqrt{2}}}\\&=\displaystyle \frac{{2\sqrt{2}i}}{2}\\&=\sqrt{2}i\end{align*}[/latex]

Back to Exercise 1.2

Exercise 1.3

1. .
   [latex]\scriptsize \begin{align*}(-2-4i)+(1+6i)&=(-2+1)+(-4+6)i\\&=-1+2i\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}(-5+3i)-(6-i)&=-5+3i-6+i\\&=(-5-6)+(3+1)i\\&=-1-5i\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*}(2-3i)-(3+2i)&=2-3i-3-2i\\&=(2-3)+(-3-2)i\\&=-1+2i\end{align*}[/latex]/li>
4. .
   [latex]\scriptsize \begin{align*}(-4+4i)-(-6+9i)&=-4+4i+6-9i\\&=(-4+6)+(4-9)i\\&=2-5i\end{align*}[/latex]
5. .
   [latex]\scriptsize \begin{align*}(5+4i)-(3+2i)-(8-7i)&=5+4i-3-2i-8+7i\\&=(5-3-8)+(4-2+7)i\\&=-6+9i\end{align*}[/latex]
6. .
   [latex]\scriptsize \begin{align*}\sqrt{{-12}}+\sqrt{{-27}}&=\sqrt{{12}}i+\sqrt{{27}}i\\&=2\sqrt{3}i+3\sqrt{3}i\\&=5\sqrt{3}i\end{align*}[/latex]
7. .
   [latex]\scriptsize \begin{align*}\sqrt{{-32}}-\sqrt{{-48}}&=\sqrt{{32}}i-\sqrt{{48}}i\\&=4\sqrt{2}i-4\sqrt{3}i\end{align*}[/latex]

Back to Exercise 1.3

Exercise 1.4

1. .
   [latex]\scriptsize \begin{align*}(3-4i)(2+3i)&=6+9i-8i-12{{i}^{2}}\\&=6+i+12\\&=18+i\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}(2+3i)(4-i)&=8-2i+12i-3{{i}^{2}}\\&=8+10i+3\\&=11+10i\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*}(-1+2i)(-2+3i)&=2-3i-4i+6i^2\\&=2-7i-6\\&=-4-7i\end{align*}[/latex]
4. .
   [latex]\scriptsize \begin{align*}{{(4+3i)}^{2}}&=(4+3i)(4+3i)\\&=16+12i+12i+9{{i}^{2}}\\&=16+24i-9\\&=7+24i\end{align*}[/latex]
5. .
   [latex]\scriptsize \begin{align*}(3+4i)(3-4i)&=9-12i+12i-16i^2\\&=9+16\\&=25\end{align*}[/latex]
   This is similar to a difference of two squares.
6. .
   [latex]\scriptsize \begin{align*}\left(3-\sqrt{-12}\right)\left(5+\sqrt{-27}\right)&=\left(3-2\sqrt{3}i\right)\left(5+3\sqrt{3}i\right)\\ &=15+9\sqrt{3}i-10\sqrt{3}i-18i^2\\ &=15-\sqrt{3}i+18\\ &=33-\sqrt{3}i\end{align*}[/latex]

Back to Exercise 1.4

Exercise 1.5

1. .
   [latex]\scriptsize \begin{align*} \displaystyle \frac{3}{5+2i}&=\displaystyle \frac{3}{5+2i}\times \displaystyle \frac{5-2i}{5-2i}\\ &=\displaystyle \frac{15-6i}{25-4i^2}\\ &=\displaystyle \frac{15-6i}{29}\\ &=\displaystyle \frac{15}{29}-\displaystyle \frac{6}{29}i\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*} \displaystyle \frac{5+3i}{4i}&=\displaystyle \frac{5+3i}{4i}\times \displaystyle \frac{4i}{4i}\\ &=\displaystyle \frac{20i+12i^2}{16i^2}\\ &=\displaystyle \frac{-12+20i}{-16}\\ &=\displaystyle \frac{3}{4}-\displaystyle \frac{5}{4}i\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*} \displaystyle \frac{2+\sqrt{-12}}{\sqrt{-5}}&=\displaystyle \frac{2+2\sqrt{3}i}{\sqrt{5}i}\\ &=\displaystyle \frac{\left(2+2\sqrt{3}i\right)}{5i}\times \displaystyle \frac{5i}{5i}\\ &=\displaystyle \frac{2\sqrt{5}i+2\sqrt{15}i^2}{5i^2}\\ &=\displaystyle \frac{-2\sqrt{15}+2\sqrt{5}i}{-5}\\ &=\displaystyle \frac{2\sqrt{15}}{5}-\displaystyle \frac{2\sqrt{5}i}{5} \end{align*}[/latex]
4. .
   [latex]\scriptsize[/latex]
5. .
   [latex]\scriptsize \begin{align*}\displaystyle \frac{{-\sqrt{{-4}}-4\sqrt{{-25}}}}{{5+i}}&=\displaystyle \frac{{-2i-20i}}{{5+i}}\\&=\displaystyle \frac{{(-22i)}}{{(5+i)}}\times \displaystyle \frac{{(5-i)}}{{(5-i)}}\\&=\displaystyle \frac{{-110i+22{{i}^{2}}}}{{25-{{i}^{2}}}}\\&=\displaystyle \frac{{-22-110i}}{{26}}\\&=-\displaystyle \frac{{11}}{{13}}-\displaystyle \frac{{55}}{{13}}i\end{align*}[/latex]
6. .
   [latex]\scriptsize \begin{align*}\displaystyle \frac{{(1+3i)(2-4i)}}{{1+2i}}&=\displaystyle \frac{{2-4i+6i-12{{i}^{2}}}}{{1+2i}}\\&=\displaystyle \frac{{2+2i+12}}{{1+2i}}\\&=\displaystyle \frac{{(14+2i)}}{{(1+2i)}}\times \displaystyle \frac{{(1-2i)}}{{(1-2i)}}\\&=\displaystyle \frac{{14-28i+2i-4{{i}^{2}}}}{{1-4{{i}^{2}}}}\\&=\displaystyle \frac{{14-26i+4}}{5}\\&=\displaystyle \frac{{18-26i}}{5}\\&=\displaystyle \frac{{18}}{5}-\displaystyle \frac{{26}}{5}i\end{align*}[/latex]
7. .
   [latex]\scriptsize \begin{align*}\displaystyle \frac{{4+i}}{i}+\displaystyle \frac{{3-4i}}{{1-i}}&=\displaystyle \frac{{(4+i)(1-i)+i(3-4i)}}{{i(1-i)}}&& \text{LCD: }i(1-i)\\ &=\displaystyle \frac{{4-4i+i-{{i}^{2}}+3i-4{{i}^{2}}}}{{i-{{i}^{2}}}}\\ &=\displaystyle \frac{{4-3i+1+3i+4}}{{i+1}}\\ &=\displaystyle \frac{9}{{(1+i)}}\times \displaystyle \frac{{(1-i)}}{{(1-i)}}\\ &=\displaystyle \frac{{9-9i}}{{1-{{i}^{2}}}}\\ &=\displaystyle \frac{{9-9i}}{2}\\ &=\displaystyle \frac{9}{2}-\displaystyle \frac{9}{2}i\end{align*}[/latex]

Back to Exercise 1.5

Unit 1: Assessment

1. .
   [latex]\scriptsize \begin{align*}(3-4i)+(2+5i)&=3-4i+2+5i\\&=5+i\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}\left( {5-\sqrt{{-50}}} \right)-\left( {3-\sqrt{{-8}}} \right)&=5-\sqrt{{50}}i-3+\sqrt{8}i\\&=5-5\sqrt{2}i-3+2\sqrt{2}i\\&=2-3\sqrt{2}i\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*}\left(5-\sqrt{-50}\right)\left(3-\sqrt{-8}\right)&=\left(5-\sqrt{50}i\right)\left(3-\sqrt{8}i\right)\\ &=\left(5-5\sqrt{2}i\right)\left(3-2\sqrt{2}i\right)\\ &=15-10\sqrt{2}i-15\sqrt{2}i+10\cdot2i^2\\ &=15-25\sqrt{2}i-20\\ &=-5-25\sqrt{2}i\end{align*}[/latex]
4. .
   [latex]\scriptsize \begin{align*}(-5+7i)-(-11+2i)+(-3-6i)^2&=-5+7i+11=2i+(-3-6i)(-3-6i)\\ &=6+5i+9+18i+18i+36i^2\\ &=15+41i-36\\ &=-21+41i\end{align*}[/latex]
5. .
   [latex]\scriptsize \begin{align*}(-3-5i)^2\cdot 6i&=(-3-5i)(-3-5i)\cdot6i\\ &=(9+15i+15i+25i^2)\cdot 6i\\ &=(9+30i-25)\cdot6i\\ &=(-16+30i)\cdot6i\\ &=-96i+180i^2\\ &=180-96i\end{align*}[/latex]
6. .
   [latex]\scriptsize \begin{align*}\displaystyle \frac{{4-8i}}{{3-\sqrt{3}i}}&=\displaystyle \frac{{\left( {4-8i} \right)}}{{\left( {3-\sqrt{3}i} \right)}}\times \displaystyle \frac{{\left( {3+\sqrt{3}i} \right)}}{{\left( {3+\sqrt{3}i} \right)}}\\&=\displaystyle \frac{{12+4\sqrt{3}i-24i-8\sqrt{3}{{i}^{2}}}}{{9-3{{i}^{2}}}}\\&=\displaystyle \frac{{12+4\sqrt{3}i-24i+8\sqrt{3}}}{{9+3}}\\&=\displaystyle \frac{{12+8\sqrt{3}+4\sqrt{3}i-24i}}{{12}}\\&=\displaystyle \frac{{4\left( {3+2\sqrt{3}} \right)+4\left( {\sqrt{3}-6} \right)i}}{{12}}\\&=\displaystyle \frac{{4\left( {3+2\sqrt{3}} \right)}}{{12}}+\displaystyle \frac{{4\left( {\sqrt{3}-6} \right)}}{{12}}i\\&=\displaystyle \frac{{3+2\sqrt{3}}}{3}+\displaystyle \frac{{\left( {\sqrt{3}-6} \right)}}{3}i\end{align*}[/latex]
7. .
   [latex]\scriptsize \begin{align*}(2+i)^2-(3-i)^2&=(2+i)(2+i)-(3-i)(3-i)\\ &=4+2i+2i+i^2-(9-3i-3i+i^2)\\ &=4+4i-1-9+6i+1\\ &=-5+10i\end{align*}[/latex]
8. .
   [latex]\scriptsize \begin{align*}\left(-1+\sqrt{-3}\right)^2&=\left(-1+\sqrt{-3}\right)\left(-1+\sqrt{-3}\right)\\ &=1-\sqrt{3}i-\sqrt{3}i+3i^2\\ &=1-2\sqrt{3}i-3\\ &=-2-2\sqrt{3}i\end{align*}[/latex]
9. .
   [latex]\scriptsize \begin{align*}i^2(2+7i)+i(3-6i)-16-i&=2i^2+7i^3+3i-6i^2-16-i\\ &=-2-7i+3i+6-16-i\\ &=-12-5i\end{align*}[/latex]
10. .
    [latex]\scriptsize \begin{align*}&\displaystyle \frac{{3-2i}}{{1+i}}-\displaystyle \frac{{1-3i}}{{1-i}}\quad \text{LCD: }(1+i)(1-i)\\&=\displaystyle \frac{{(3-2i)(1-i)-(1-3i)(1+i)}}{{(1+i)(1-i)}}\\&=\displaystyle \frac{{3-3i-2i+2{{i}^{2}}-(1+i-3i-3{{i}^{2}})}}{{1-{{i}^{2}}}}\\&=\displaystyle \frac{{3-3i-2i+2{{i}^{2}}-1-i+3i+3{{i}^{2}}}}{{1+1}}\\&=\displaystyle \frac{{2-3i-2-3}}{2}\\&=\displaystyle \frac{{-3-3i}}{2}\\&=-\displaystyle \frac{3}{2}-\displaystyle \frac{3}{2}i\end{align*}[/latex]

Back to Unit 1: Assessment