Space, shape and measurement: Use the Cartesian co-ordinate system to derive and apply equations
Unit 1: Determine the equation of a circle with any centre
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Find the equation of a circle centred at the origin.
- Find the equation of a circle with centre [latex]\scriptsize (a,b)[/latex].
- Write the equation of the circle in standard form.
What you should know
Before you start this unit, make sure you can:
- State the theorem of Pythagoras for right-angled triangles. Refer to level 2 subject outcome 3.3 unit 2 if you need help with this.
- Calculate the distance between two points on the Cartesian plane. Refer to level 2 subject outcome 3.3 unit 2 if you need help with this.
- Calculate the midpoint of a line segment between two points on the Cartesian plane. Refer to level 2 subject outcome 3.3 unit 2 if you need help with this.
- Use the Cartesian coordinate system to derive the equation of a straight line through two given points using the gradient-point form or the gradient-intercept form. Refer to level 3 subject outcome 3.2 unit 1 if you need help with this.
- Complete the square of a quadratic expression. Refer to level 3 subject outcome 2.2 unit 3 if you need help with this.
- Find the coordinates of a point [latex]\scriptsize (x,y)[/latex] after it has been reflected about the axes and lines [latex]\scriptsize y=x[/latex] and [latex]\scriptsize y=-x[/latex]. Refer to level 2 subject outcome 3.4 unit 1 if you need help with this.
Introduction
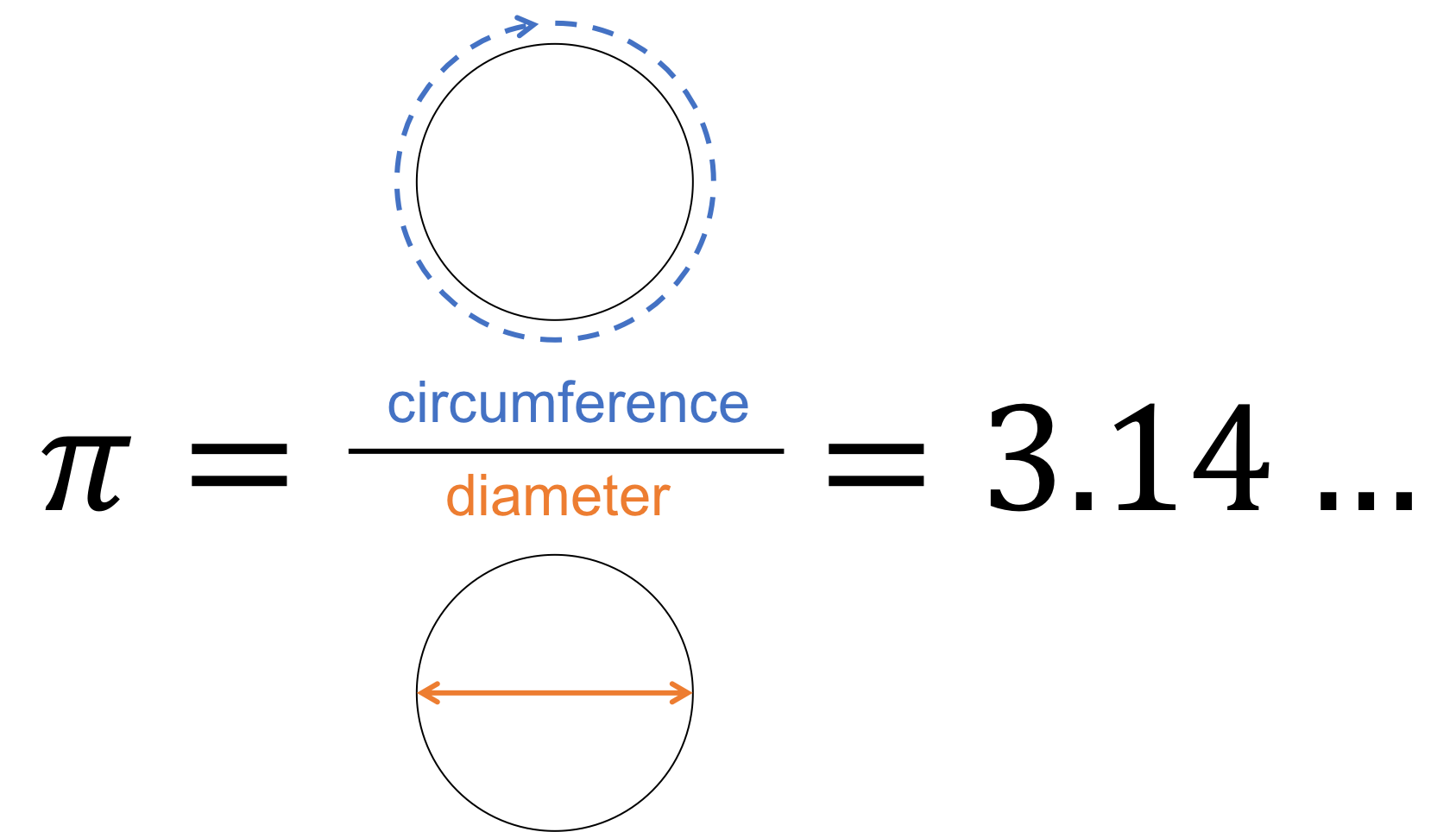
The circle is one of the most common and important geometric shapes in mathematics. It is, after all, what defines one of the most famous numbers in the world, [latex]\scriptsize \pi[/latex] (pi). [latex]\scriptsize \pi[/latex], remember, is the ratio of a circle’s circumference to its diameter (see figure 1) and it pops up in all sorts of interesting and useful places.
The circle, and in particular the unit circle (circle with a radius of [latex]\scriptsize 1[/latex] centred on the origin), is also foundational to trigonometry which is a key link between algebra and geometry.
So, I think you will agree, the circle is important.
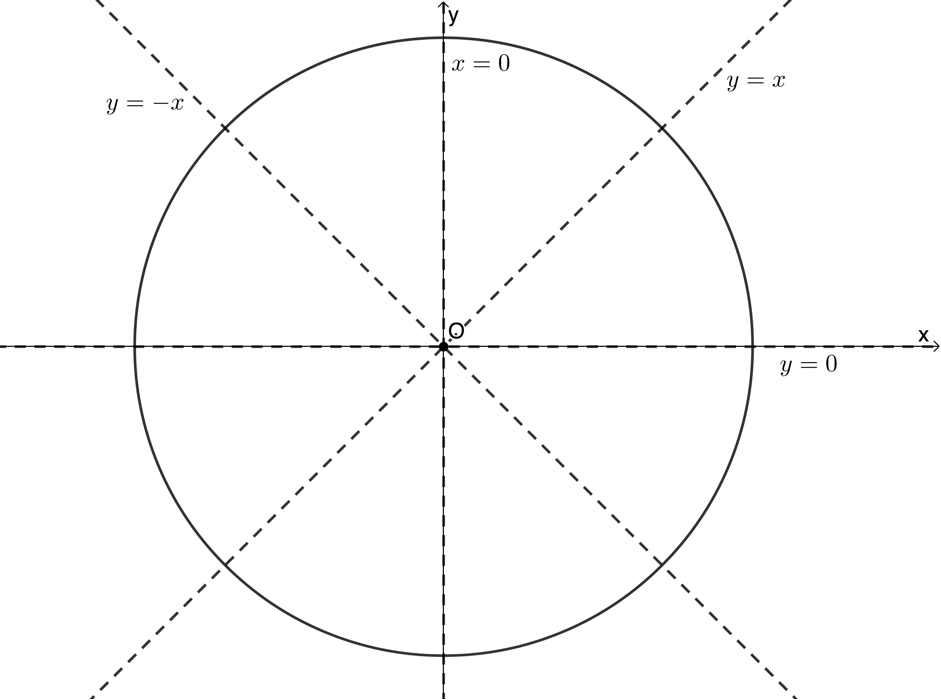
However, we did not deal with it when examining functions, because it is not a function. The circle fails the basic test of a function – the vertical line test. Draw any circle on the Cartesian plane and it is easy to see why. Except for two points on each side of the circle, a vertical line cuts the circle twice (see figure 2). Therefore, almost all of the input values correspond to more than one output value.
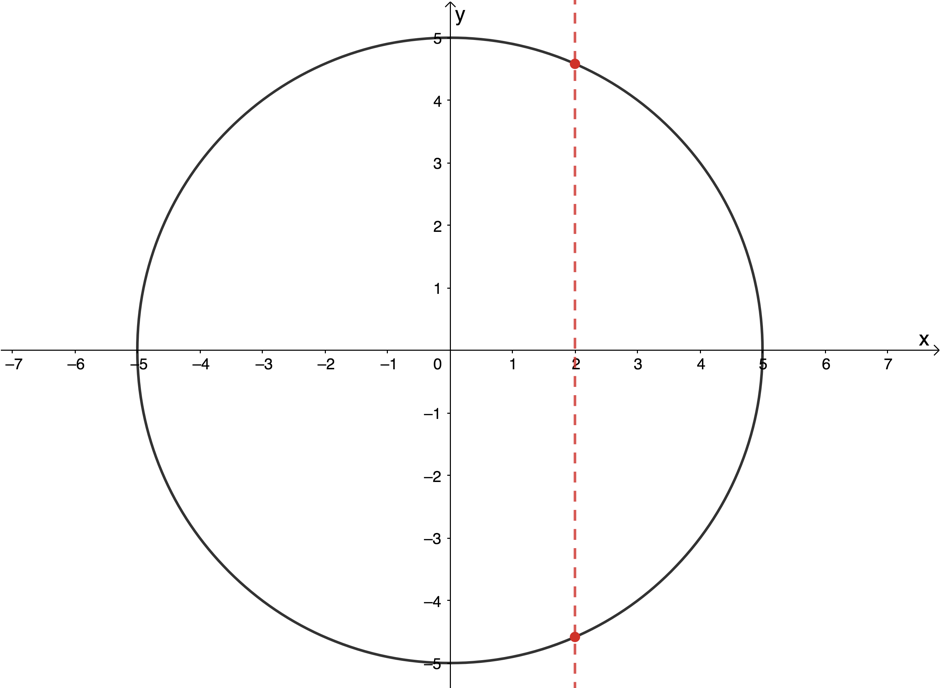
But just because the circle is not a function does not mean that there is not a relation that relates all the input and output pairs that together make up the circle. In this unit we will discover what this equation is.
The equation of a circle with centre the origin
By definition, a circle is a flat shape consisting of all the points in a plane that are an equal distance away from its centre. In other words, every point on the circumference of a circle is the same distance (equidistant) from its centre.
You might already know what the equation is for a circle centred on the origin. If not, complete activity 1.1 to find out.
Activity 1.1: Find the equation of a circle
Time required: 15 minutes
What you need:
- a pen or pencil
- a blank piece of paper or graph paper
What to do:
For this activity, you will need to draw a system of axes. Use a scale of [latex]\scriptsize 1\ \text{cm}=1\ \text{unit}[/latex] and make sure your axes extend about [latex]\scriptsize 5[/latex] units in all directions.
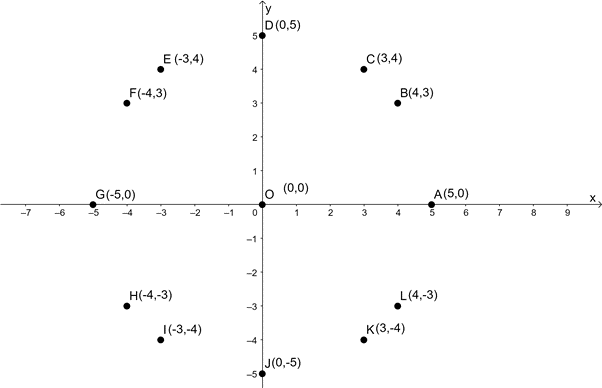
- Plot the following points on your Cartesian plane:
[latex]\scriptsize O(0,0)[/latex], [latex]\scriptsize A(5,0)[/latex], [latex]\scriptsize B(4,3)[/latex], [latex]\scriptsize C(3,4)[/latex], [latex]\scriptsize D(0,5)[/latex], [latex]\scriptsize E(-3,4)[/latex], [latex]\scriptsize F(-4,3)[/latex], [latex]\scriptsize G(-5,0)[/latex], [latex]\scriptsize H(-4,-3)[/latex], [latex]\scriptsize \displaystyle I(-3,-4)[/latex] [latex]\scriptsize J(0,-5)[/latex], [latex]\scriptsize K(3,-4)[/latex], [latex]\scriptsize L(4,-3)[/latex] - Determine the following distances using the distance formula [latex]\scriptsize d=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}[/latex]:
[latex]\scriptsize OA[/latex], [latex]\scriptsize OB[/latex], [latex]\scriptsize OC[/latex], [latex]\scriptsize OD[/latex], [latex]\scriptsize OE[/latex], [latex]\scriptsize OF[/latex], [latex]\scriptsize OG[/latex], [latex]\scriptsize OH[/latex], [latex]\scriptsize OI[/latex], [latex]\scriptsize OJ[/latex], [latex]\scriptsize OK[/latex], [latex]\scriptsize OL[/latex] - What do you notice about the length of each line segment? What general term could we give to these line segments?
- What object do these points form if you join them up with a smooth curve?
- If the point [latex]\scriptsize P(x,y)[/latex] lies on this shape, use the distance formula to determine an expression for the length of [latex]\scriptsize OP[/latex].
- Can you deduce an equation for a circle centre the origin?
What did you find?
- Plot the following points on your Cartesian plane:
- [latex]\scriptsize OA=\sqrt{{{{{(5-0)}}^{2}}+{{{(0-0)}}^{2}}}}=\sqrt{{25}}=5[/latex]
[latex]\scriptsize OB=\sqrt{{{{{(4-0)}}^{2}}+{{{(3-0)}}^{2}}}}=\sqrt{{16+9}}=\sqrt{{25}}=5[/latex]
[latex]\scriptsize OC=\sqrt{{{{{(3-0)}}^{2}}+{{{(4-0)}}^{2}}}}=\sqrt{{9+16}}=\sqrt{{25}}=5[/latex]
[latex]\scriptsize OD=\sqrt{{{{{(0-0)}}^{2}}+{{{(5-0)}}^{2}}}}\sqrt{{25}}=5[/latex]
[latex]\scriptsize OE=\sqrt{{{{{(-3-0)}}^{2}}+{{{(4-0)}}^{2}}}}=\sqrt{{9+16}}=\sqrt{{25}}=5[/latex]
[latex]\scriptsize OF=\sqrt{{{{{(-4-0)}}^{2}}+{{{(3-0)}}^{2}}}}=\sqrt{{16+9}}=\sqrt{{25}}=5[/latex]
[latex]\scriptsize OG=\sqrt{{{{{(-5-0)}}^{2}}+{{{(0-0)}}^{2}}}}=\sqrt{{25}}=5[/latex]
[latex]\scriptsize OH=\sqrt{{{{{(-4-0)}}^{2}}+{{{(-3-0)}}^{2}}}}=\sqrt{{16+9}}=\sqrt{{25}}=5[/latex]
[latex]\scriptsize OI=\sqrt{{{{{(-3-0)}}^{2}}+{{{(-4-0)}}^{2}}}}=\sqrt{{9+16}}=\sqrt{{25}}=5[/latex]
[latex]\scriptsize OJ=\sqrt{{{{{(0-0)}}^{2}}+{{{(-5-0)}}^{2}}}}=\sqrt{{25}}=5[/latex]
[latex]\scriptsize OK=\sqrt{{{{{(3-0)}}^{2}}+{{{(-4-0)}}^{2}}}}=\sqrt{{9+16}}=\sqrt{{25}}=5[/latex]
[latex]\scriptsize OL=\sqrt{{{{{(4-0)}}^{2}}+{{{(-3-0)}}^{2}}}}=\sqrt{{16+9}}=\sqrt{{25}}=5[/latex] - Each of the line segments is the same length ([latex]\scriptsize 5\ \text{units}[/latex]). We could call these line segments the radius of a circle.
- They all form a circle.
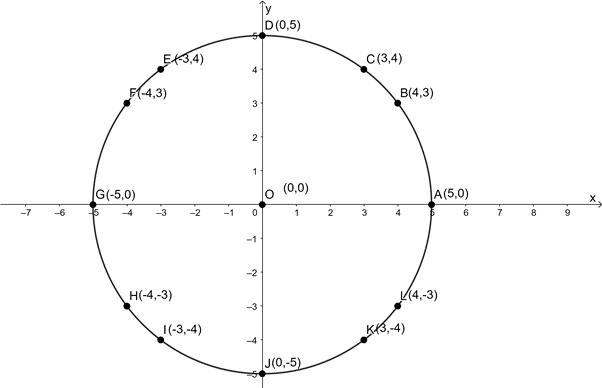
- [latex]\scriptsize OP=\sqrt{{{{{(x-0)}}^{2}}+{{{(y-0)}}^{2}}}}=\sqrt{{{{x}^{2}}+{{y}^{2}}}}[/latex].
- Since [latex]\scriptsize OP[/latex] is the radius ([latex]\scriptsize r[/latex]) of the circle:
[latex]\scriptsize r=\sqrt{{{{x}^{2}}+{{y}^{2}}}}[/latex] or [latex]\scriptsize {{r}^{2}}={{x}^{2}}+{{y}^{2}}[/latex]
We have the equation of a circle centre the origin.
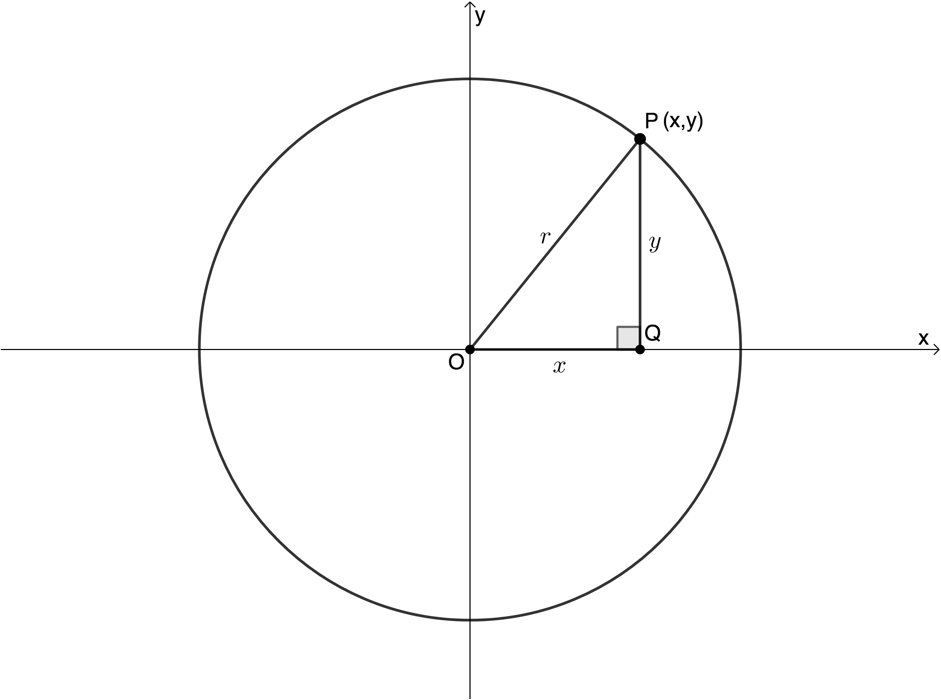
In activity 1.1 we discovered what the equation of a circle centre the origin is. This equation is based on the theorem of Pythagoras (see figure 3).
In [latex]\scriptsize \Delta OPQ[/latex]:
[latex]\scriptsize \begin{align*}O{{P}^{2}}&=O{{Q}^{2}}+P{{Q}^{2}}\quad \text{(Pythagoras)}\\\text{But }OP&=r\text{ and }OQ=x-0\text{ and }PQ=y-0\\\therefore {{r}^{2}}&={{(x-0)}^{2}}+{{(y-0)}^{2}}\\\therefore {{r}^{2}}&={{x}^{2}}+{{y}^{2}}\end{align*}[/latex]
Equation of a circle centre the origin:
[latex]\scriptsize {{x}^{2}}+{{y}^{2}}={{r}^{2}}[/latex]
Example 1.1
A circle with centre the origin has a radius of [latex]\scriptsize 3\text{ units}[/latex].
- Determine the equation of the circle.
- Sketch the circle on the Cartesian plane.
- Show that the point [latex]\scriptsize (-\sqrt{4},\sqrt{5})[/latex] lies on the circle.
Solutions
- The circle has its centre the origin. Therefore, its equation is [latex]\scriptsize {{x}^{2}}+{{y}^{2}}={{r}^{2}}[/latex]. We are told that the radius is [latex]\scriptsize 3\text{ units}[/latex]. Therefore, the equation is [latex]\scriptsize {{x}^{2}}+{{y}^{2}}={{(3)}^{2}}[/latex] or [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=9[/latex].
- We know that the centre is the origin and the radius is [latex]\scriptsize 3\text{ units}[/latex]. Therefore, the circle will pass through the points [latex]\scriptsize (3,0)[/latex], [latex]\scriptsize (0,3)[/latex], [latex]\scriptsize (-3,0)[/latex] and [latex]\scriptsize (0,-3)[/latex].
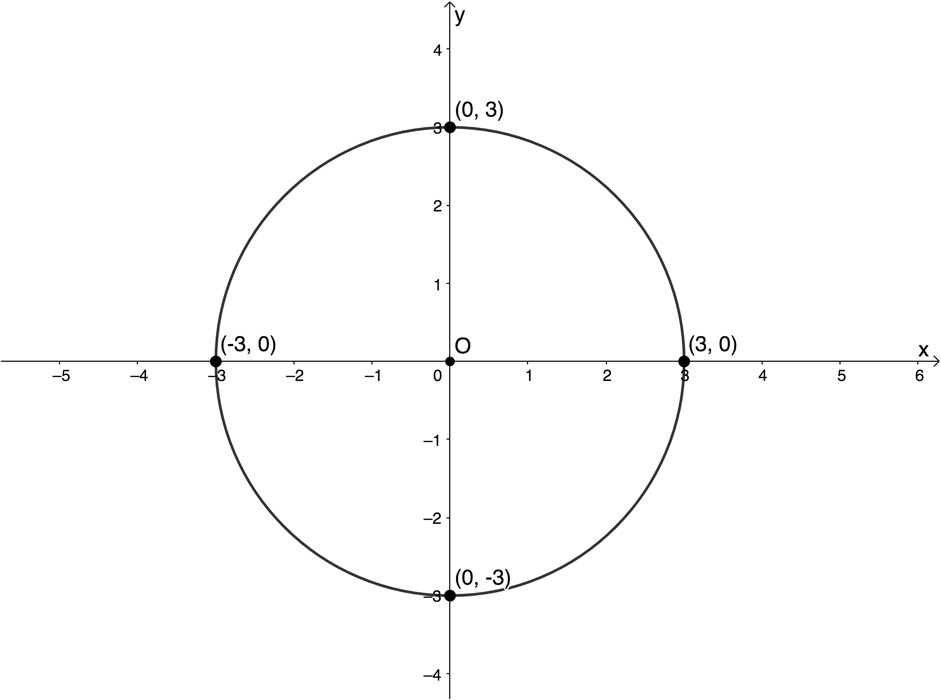
- The equation of the circle is [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=9[/latex]. Does the point [latex]\scriptsize (-\sqrt{4},\sqrt{5})[/latex] satisfy the equation?
[latex]\scriptsize \begin{align*}\text{LHS}&={{x}^{2}}+{{y}^{2}}\\&={{\left( {-\sqrt{4}} \right)}^{2}}+{{\left( {\sqrt{5}} \right)}^{2}}\\&=4+5\\&=9=\text{RHS}\end{align*}[/latex]
Therefore, the point does lie on the circle.
Example 1.2
A circle centre the origin passes through the points [latex]\scriptsize A(-6,6)[/latex] and [latex]\scriptsize B(6,-6)[/latex].
- Plot the points and draw a rough sketch of the circle.
- Determine the equation of the circle.
- Calculate the length of [latex]\scriptsize AB[/latex].
- Explain why [latex]\scriptsize AB[/latex] is a diameter of the circle.
Solutions
- Here is a sketch of the circle:
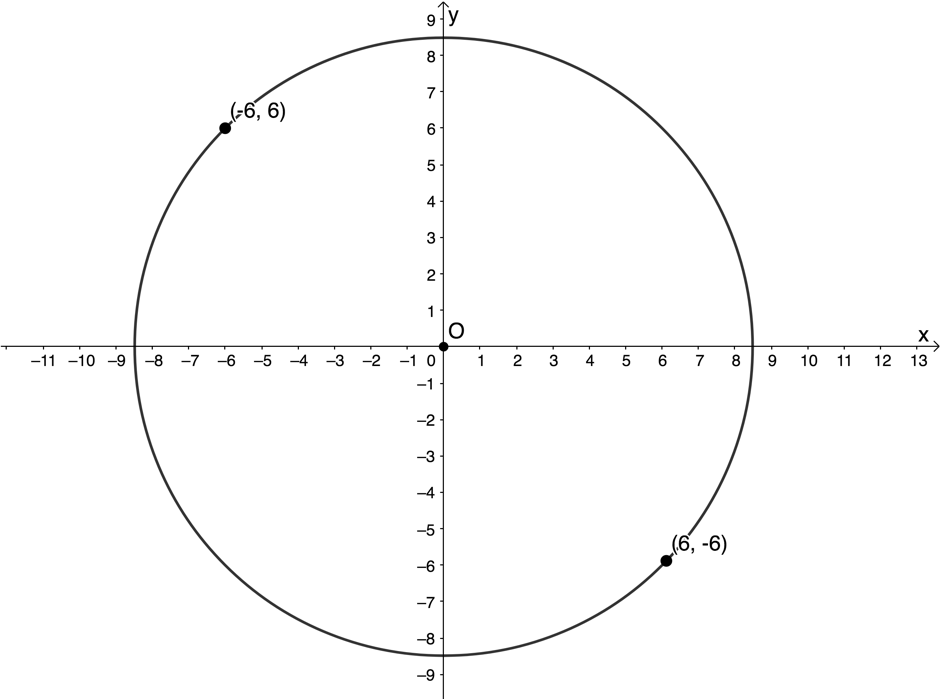
- [latex]\scriptsize {{x}^{2}}+{{y}^{2}}={{r}^{2}}[/latex]. We have two possible points we can substitute into the equation. We will substitute [latex]\scriptsize A(-6,6)[/latex].
[latex]\scriptsize \begin{align*}{{x}^{2}}+{{y}^{2}} & ={{r}^{2}}\\\therefore {{(-6)}^{2}}+{{6}^{2}} & ={{r}^{2}}\\\therefore 36+36 & ={{r}^{2}}\\\therefore {{r}^{2}} & =72\end{align*}[/latex]
The equation of the circle is [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=72[/latex]. - .
[latex]\scriptsize \begin{align*}{{d}_{{AB}}}&=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}\\&=\sqrt{{{{{(-6-6)}}^{2}}+{{{(6-(-6))}}^{2}}}}\\&=\sqrt{{{{{(-12)}}^{2}}+{{{12}}^{2}}}}\\&=\sqrt{{144+144}}\\&=\sqrt{{288}}\\&=2\sqrt{{72}}\end{align*}[/latex] - The radius of the circle is [latex]\scriptsize \sqrt{{72}}[/latex]. Therefore, [latex]\scriptsize AB[/latex] is twice the radius of the circle. Also, a circle centre the origin is symmetrical about the axes as well as about the lines [latex]\scriptsize y=x[/latex] and [latex]\scriptsize y=-x[/latex]. The points [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex] are symmetrical about the line [latex]\scriptsize y=-x[/latex] meaning that [latex]\scriptsize AB[/latex] passes through the centre. Therefore, [latex]\scriptsize AB[/latex] is a straight line passing through the centre and twice the radius i.e. [latex]\scriptsize AB[/latex] is the diameter.
.
Note: You could also find the equation of [latex]\scriptsize AB[/latex] and then show that the point [latex]\scriptsize O(0,0)[/latex] lies on this point to demonstrate that [latex]\scriptsize AB[/latex] passes through the centre. In both cases, showing that a line is a diameter requires you to show that it is:
- a straight line passing through the centre of the circle
- twice the length of the radius.
An important characteristic of the circle centre the origin is its symmetry. The shape is very symmetrical. It is symmetrical about both axes as well as about the lines [latex]\scriptsize y=x[/latex] and [latex]\scriptsize y=-x[/latex].
Take note!
Take note!
To prove that a line is a diameter you must prove that it is:
- a straight line passing through the centre of the circle
- twice the length of the radius.
Exercise 1.1
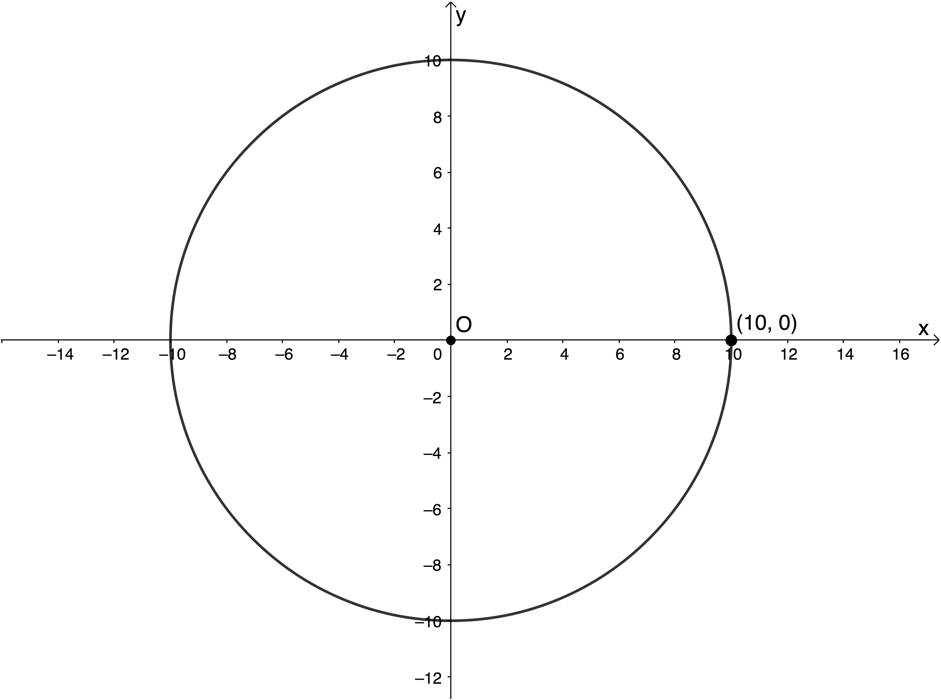
- Given [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=100[/latex]:
- Determine the radius.
- Make a sketch of the circle.
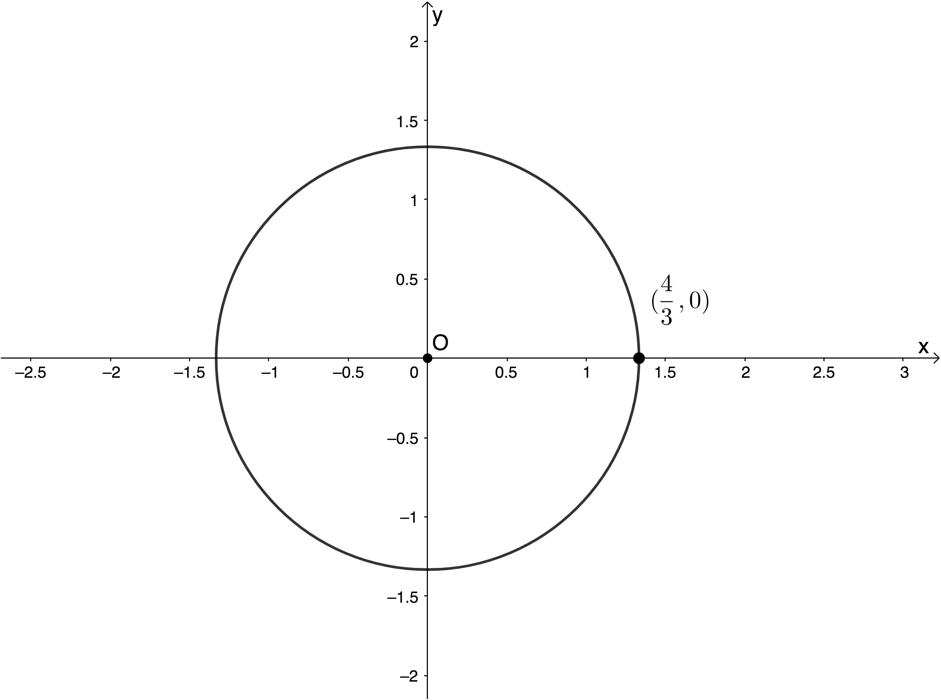
- Given [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=\displaystyle \frac{{16}}{9}[/latex]:
- Determine the radius.
- Make a sketch of the circle.
- Given [latex]\scriptsize 4{{x}^{2}}+4{{y}^{2}}=80[/latex]:
- Determine the radius.
- Make a sketch of the circle.
- Determine the equation of the circle in each case:
- With centre the origin and a radius of [latex]\scriptsize 6[/latex].
- With centre [latex]\scriptsize (0,0)[/latex] and [latex]\scriptsize r=\sqrt{{13}}[/latex].
- With centre the origin passing through [latex]\scriptsize (-3,-7)[/latex].
- Passing through [latex]\scriptsize (2s,3s)[/latex] and with centre [latex]\scriptsize (0,0)[/latex].
- .
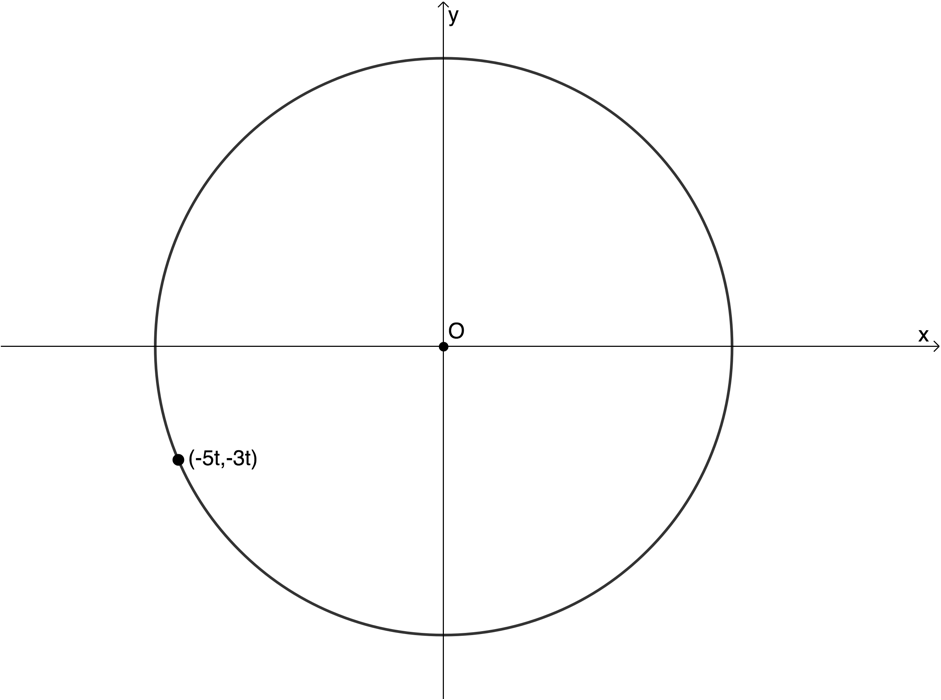
- Is [latex]\scriptsize \sqrt{{90}}+{{x}^{2}}-{{y}^{2}}=0[/latex] the equation of a circle with centre the origin?
- Given a circle with centre the origin, with a radius of [latex]\scriptsize r=\sqrt{{50}}[/latex], determine the coordinates of the points on the circle whose x-values are three times their y-value.
The full solutions are at the end of the unit.
The equation of a circle centre [latex]\scriptsize (a,b)[/latex]
There are two ways to think about the equation of a circle with centre not the origin but any point [latex]\scriptsize (a,b)[/latex] on the Cartesian plane.
The first is to think about translating or shifting the circle centre the origin. Consider the parabola [latex]\scriptsize y=2{{x}^{2}}[/latex]. We know that the graph of [latex]\scriptsize y=2{{x}^{2}}+1[/latex] is the same as [latex]\scriptsize y=2{{x}^{2}}[/latex] except that the graph has been shifted one unit up (see figure 4).
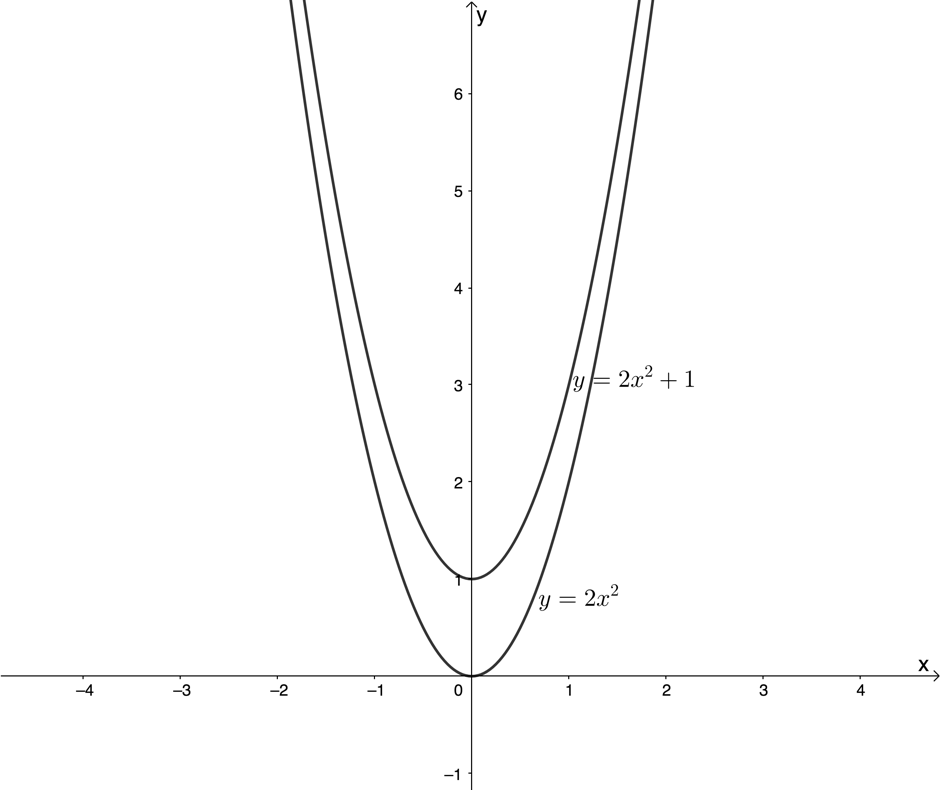
We can rewrite the equation [latex]\scriptsize y=2{{x}^{2}}+1[/latex] as [latex]\scriptsize y-1=2{{x}^{2}}[/latex] or [latex]\scriptsize (y-1)=2{{x}^{2}}[/latex].
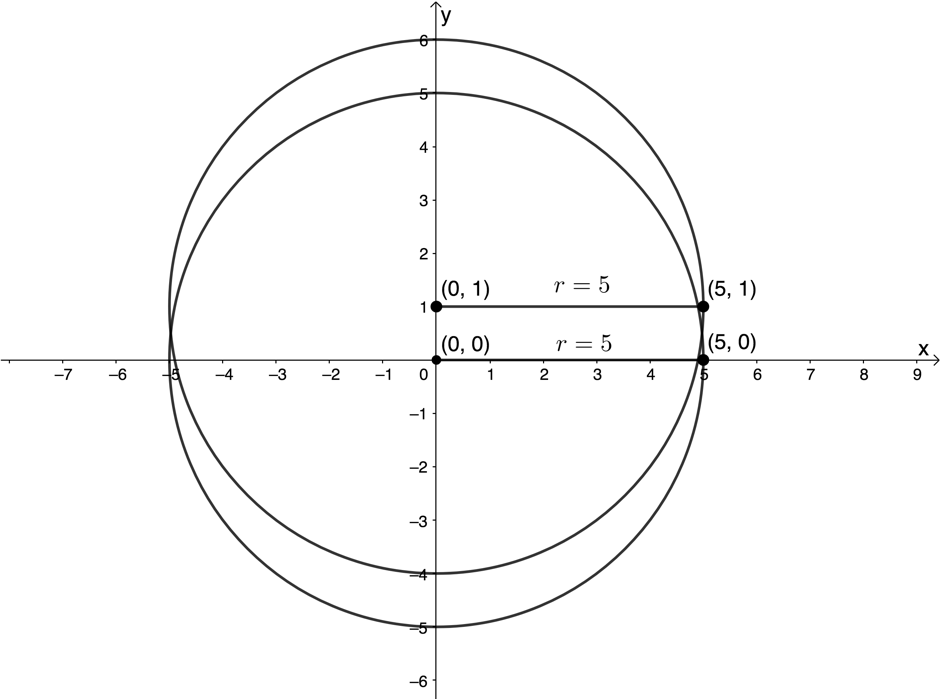
Now, how do you think the circle defined by [latex]\scriptsize {{x}^{2}}+{{(y-1)}^{2}}=25[/latex] is different from that defined by [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=25[/latex]? [latex]\scriptsize {{x}^{2}}+{{(y-1)}^{2}}=25[/latex] is the same except that the circle has been shifted one unit up and the centre is now the point [latex]\scriptsize (0,1)[/latex] (see figure 5).
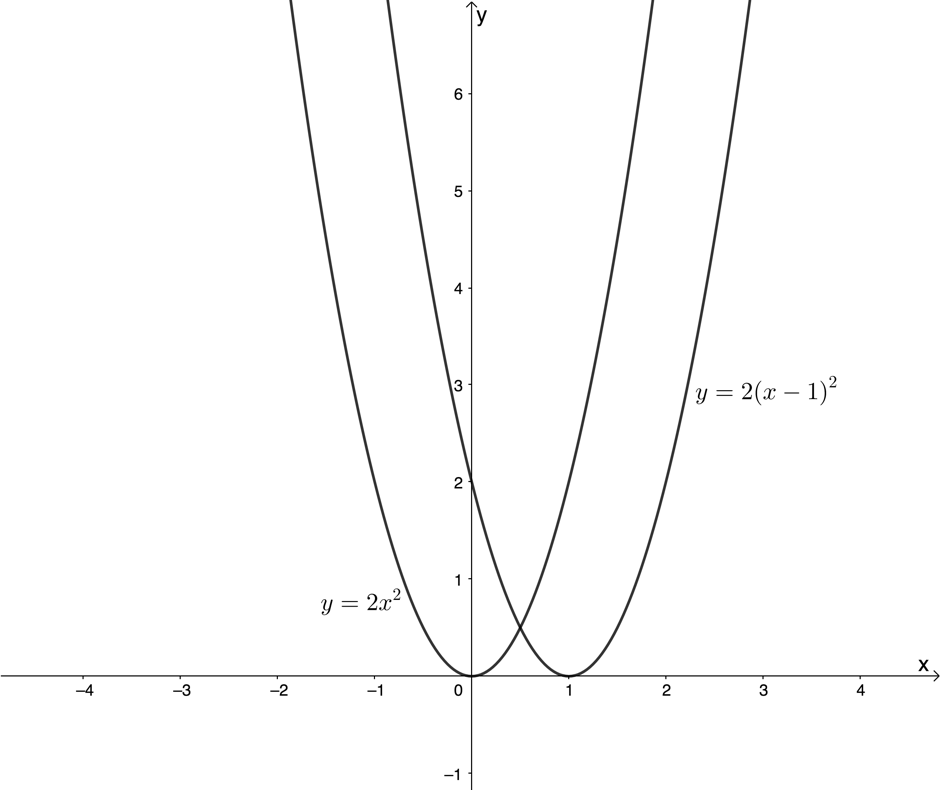
Consider the parabola [latex]\scriptsize y=2{{x}^{2}}[/latex] again. We know that the graph of [latex]\scriptsize y=2{{(x-1)}^{2}}[/latex] is the same as [latex]\scriptsize y=2{{x}^{2}}[/latex] except that it has been shifted one unit to the right (see figure 6).
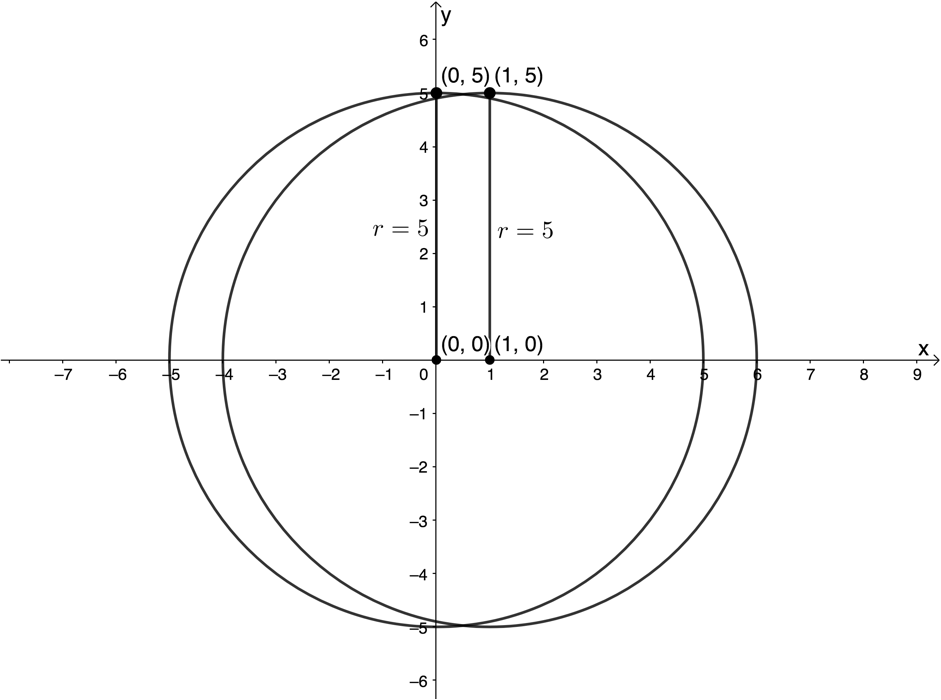
In the same way, the circle [latex]\scriptsize {{(x-1)}^{2}}+{{y}^{2}}=25[/latex] is the same as [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=25[/latex] just shifted one unit to the right. The centre is now the point [latex]\scriptsize (1,0)[/latex] (see figure 7).
Therefore, we can generalise and say that the equation [latex]\scriptsize {{(x-a)}^{2}}+{{(y-b)}^{2}}={{r}^{2}}[/latex] is the equation of a circle radius [latex]\scriptsize r[/latex] and with centre [latex]\scriptsize (a,b)[/latex].
The other way to consider this is geometrically. Figure 8 shows a circle centre [latex]\scriptsize (a,b)[/latex] and passing through [latex]\scriptsize p(x,y)[/latex] with a radius [latex]\scriptsize r[/latex].
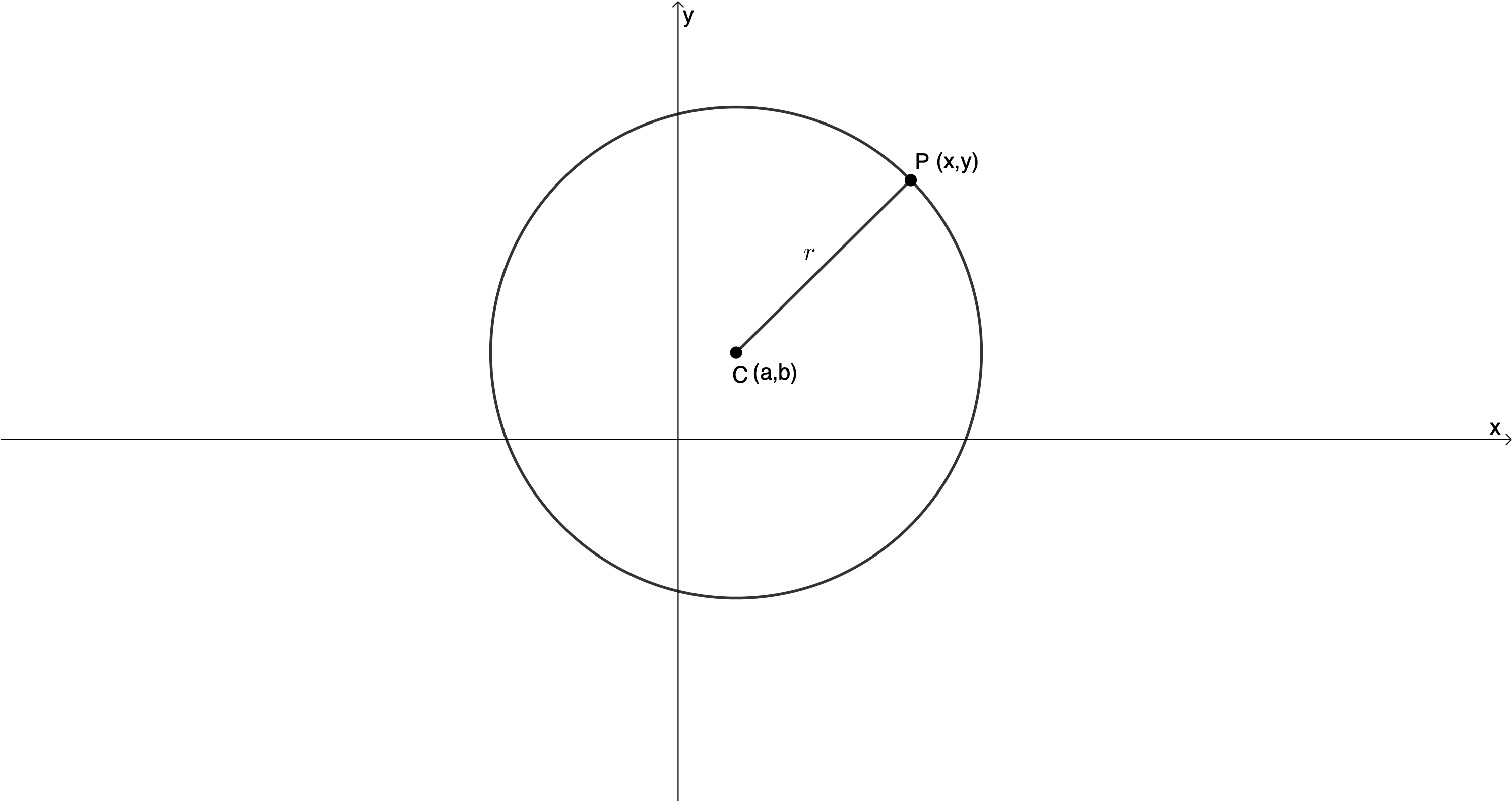
We can determine the distance [latex]\scriptsize PC[/latex] using the distance formula.
[latex]\scriptsize \begin{align*}{{d}_{{PC}}}&=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}\\&=\sqrt{{{{{(x-a)}}^{2}}+{{{(y-b)}}^{2}}}}\end{align*}[/latex]
But we know that the length of [latex]\scriptsize PC[/latex] is the radius. Therefore [latex]\scriptsize {{d}_{{PC}}}=r[/latex]. Therefore:
[latex]\scriptsize \begin{align*}r & =\sqrt{{{{{(x-a)}}^{2}}+{{{(y-b)}}^{2}}}}\\\therefore {{r}^{2}} & ={{(x-a)}^{2}}+{{(y-b)}^{2}}\\\therefore {{(x-a)}^{2}}+{{(y-b)}^{2}} & ={{r}^{2}}\end{align*}[/latex]
With this equation, we can think of the circle with centre the origin as a special case.
[latex]\scriptsize \begin{align*}{{(x-a)}^{2}}+{{(y-b)}^{2}} & ={{r}^{2}}\text{ but }(a,b)=(0,0)\\\therefore {{(x-0)}^{2}}+{{(y-0)}^{2}} & ={{r}^{2}}\\\therefore {{x}^{2}}+{{y}^{2}} & ={{r}^{2}}\end{align*}[/latex]
Equation of a circle with centre at [latex]\scriptsize (a,b)[/latex]:
[latex]\scriptsize {{(x-a)}^{2}}+{{(y-b)}^{2}}={{r}^{2}}[/latex]
Example 1.3
[latex]\scriptsize A(4,6)[/latex] is a point on a circle centre [latex]\scriptsize (3,3)[/latex]:
- Determine the equation of the circle.
- Draw a sketch of the circle.
- Does the point [latex]\scriptsize B(\displaystyle \frac{3}{2},2)[/latex] lie on the circle?
- Does the circle cut the y-axis?
Solutions
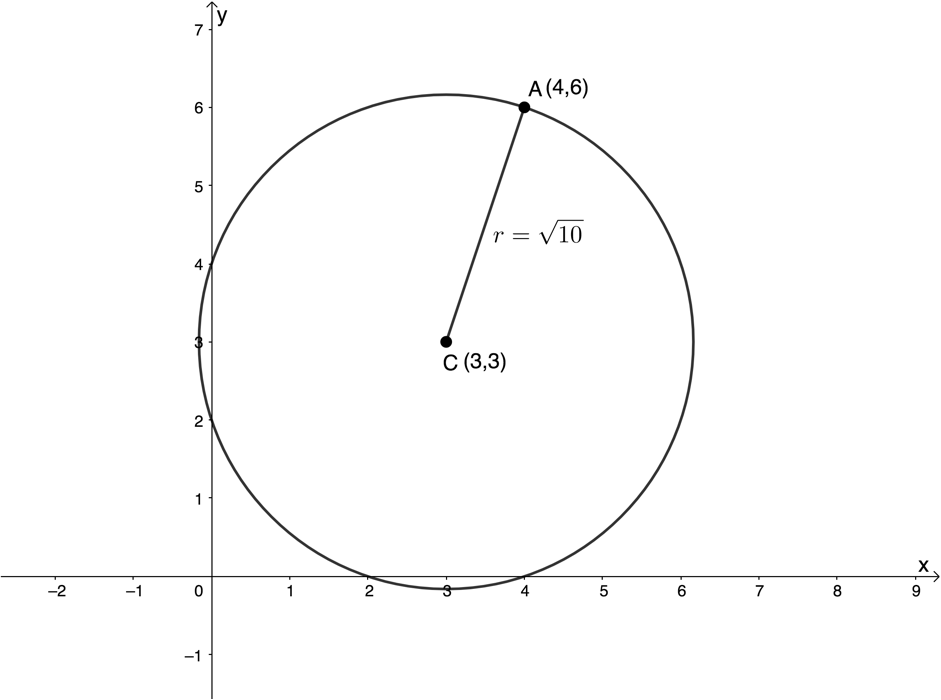
- Because the circle has centre [latex]\scriptsize (3,3)[/latex], we know that the equation will be of the form[latex]\scriptsize {{(x-3)}^{2}}+{{(y-3)}^{2}}={{r}^{2}}[/latex]. We need to find [latex]\scriptsize r[/latex] which we can do by finding the distance between the point [latex]\scriptsize A(4,6)[/latex] and the centre [latex]\scriptsize (3,3)[/latex].
[latex]\scriptsize \begin{align*}r&=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}\\&=\sqrt{{{{{(4-3)}}^{2}}+{{{(6-3)}}^{2}}}}\\&=\sqrt{{1+9}}\\&=\sqrt{{10}}\end{align*}[/latex]
Therefore, [latex]\scriptsize {{r}^{2}}=10[/latex] and the equation of the circle is [latex]\scriptsize {{(x-3)}^{2}}+{{(y-3)}^{2}}=10[/latex]. - The easiest way to draw a sketch of a circle centre [latex]\scriptsize (a,b)[/latex] and passing through a point [latex]\scriptsize (x,y)[/latex] is to use a pair of compasses. Set the point on the centre and your pencil on the point to get the radius, and draw the resulting circle.
- If the point [latex]\scriptsize B(\displaystyle \frac{3}{2},2)[/latex] lies on the circle, it will satisfy the equation of the circle.
[latex]\scriptsize \displaystyle \begin{align*}\text{LHS}&={{(x-3)}^{2}}+{{(y-3)}^{2}}\\&={{\left( {\displaystyle \frac{3}{2}-3} \right)}^{2}}+{{(2-3)}^{2}}\\&={{\left( {-\displaystyle \frac{3}{2}} \right)}^{2}}+{{(-1)}^{2}}\\&=\displaystyle \frac{9}{4}+1\\&=\displaystyle \frac{{9+4}}{4}\\&=\displaystyle \frac{{13}}{4}\ne \text{RHS}\end{align*}[/latex]
Therefore, the point [latex]\scriptsize B(\displaystyle \frac{3}{2},2)[/latex] does not lie on the circle. - For the circle to cut the y-axis, there must be a point on the circle with an x-coordinate of zero. We need to substitute [latex]\scriptsize x=0[/latex] into the equation to see if there is at least one real solution for [latex]\scriptsize y[/latex].
[latex]\scriptsize \begin{align*}{{(0-3)}^{2}}+{{(y-3)}^{2}} & =10\\\therefore {{(-3)}^{2}}+{{(y-3)}^{2}} & =10\\\therefore 9+{{y}^{2}}-6y+9 & =10\\\therefore {{y}^{2}}-6y+8 & =0\\\therefore (y-4)(y-2) & =0\\\therefore y=4\text{ } & \text{or }y=2\end{align*}[/latex]
There are two points [latex]\scriptsize (0,2)[/latex] and [latex]\scriptsize (0,4)[/latex] where the circle cuts the y-axis.
Note: You can also find any x- or y-intercepts to help you make an accurate sketch of a circle centre [latex]\scriptsize (a,b)[/latex].
Example 1.4
Determine the coordinates of the centre of the circle and its radius if the equation of the circle is [latex]\scriptsize 3{{x}^{2}}+12x+3{{y}^{2}}-24y+21=0[/latex].
Solution
This question is basically asking us to rewrite the equation of the circle centre [latex]\scriptsize (a,b)[/latex] in the standard form [latex]\scriptsize {{(x-a)}^{2}}+{{(y-b)}^{2}}={{r}^{2}}[/latex] rather than the current expanded form. Because the standard form of the equation of a circle contains perfect squares, we know that we will need to complete the squares for [latex]\scriptsize x[/latex] and for [latex]\scriptsize y[/latex].
Step 1: Get the coefficients of the [latex]\scriptsize {{x}^{2}}[/latex] and [latex]\scriptsize {{y}^{2}}[/latex] terms equal to [latex]\scriptsize 1[/latex]
[latex]\scriptsize \begin{align*}3{{x}^{2}}+12x+3{{y}^{2}}-24y+21 & =0\\\therefore {{x}^{2}}+4x+{{y}^{2}}-8y+7 & =0\end{align*}[/latex]
Step 2: Complete the squares
Remember, to complete the squares, we need to add half the coefficients of the [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex] terms squared. Don’t forget to keep the equation balanced by subtracting these values as well.
[latex]\scriptsize \begin{align*}{{x}^{2}}+4x+{{y}^{2}}-8y+7 & =0\\\therefore {{x}^{2}}+4x+4+{{y}^{2}}-8y+16+7-4-16 & =0\\\therefore {{(x+2)}^{2}}+{{(y-4)}^{2}} & =13\end{align*}[/latex]
Step 3: Answer the question
The centre of the circle is the point [latex]\scriptsize (-2,4)[/latex] and the radius is [latex]\scriptsize r=\sqrt{{13}}[/latex].
Example 1.5
Given a circle centre the origin with [latex]\scriptsize r=9[/latex]:
- Write down the equation of the circle if it is shifted [latex]\scriptsize 3\text{ units}[/latex] to the left and [latex]\scriptsize 5\text{ units}[/latex] down.
- Draw a sketch of the circle.
- Write down the equation of the circle that is symmetrical to the circle in question 1 about the line [latex]\scriptsize y=-x[/latex].
- Sketch the circle in question 3 on the same set of axes as the graph in question 2.
Solutions
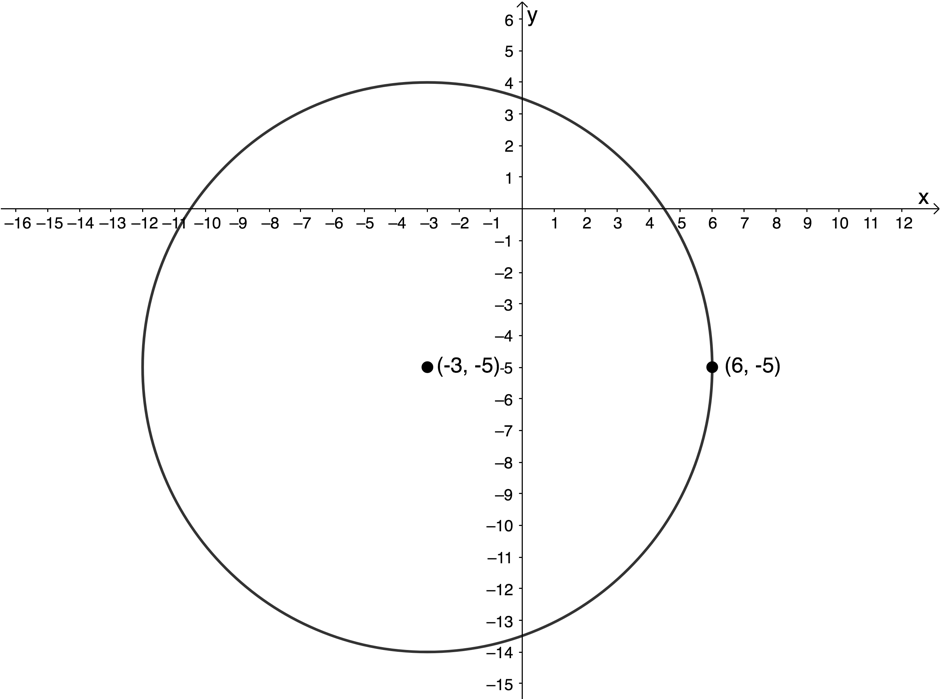
- The equation of the circle we were given is [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=81[/latex]. The equation of the shifted circle will be [latex]\scriptsize {{(x+3)}^{2}}+{{(y+5)}^{2}}=81[/latex].
- We know the centre of the circle but we need at least one point that the circle passes through. An easy way to find this point is to move either horizontally or vertically from the centre a distance of [latex]\scriptsize 9\text{ units}[/latex] (the radius) as indicated below.
- To find the coordinates of a point symmetrical about the line [latex]\scriptsize y=-x[/latex], each [latex]\scriptsize x[/latex] value must be replaced with [latex]\scriptsize -y[/latex] and each [latex]\scriptsize y[/latex] value replaced with [latex]\scriptsize -x[/latex]. Therefore, the equation of the symmetrical circle will be:
[latex]\scriptsize \begin{align*}{{\left( {(-y)+3} \right)}^{2}}+{{\left( {(-x)+5} \right)}^{2}} & =81\\\therefore {{(5-x)}^{2}}+{{(3-y)}^{2}} & =81\end{align*}[/latex]
We can expand the equation and then simplify into standard form.
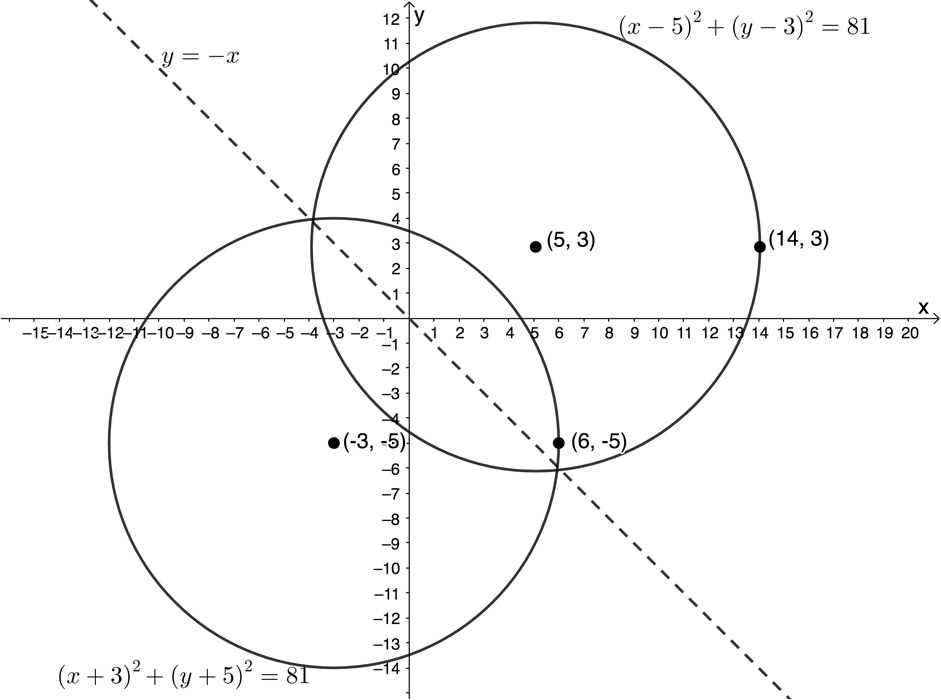
[latex]\scriptsize \begin{align*}{{(5-x)}^{2}}+{{(3-y)}^{2}} & =81\\\therefore 25-10x+{{x}^{2}}+9-6y+{{y}^{2}} & =81\\\therefore {{x}^{2}}-10x+25+{{y}^{2}}-6y+9 & =81\\\therefore {{(x-5)}^{2}}+{{(y-3)}^{2}} & =81\end{align*}[/latex] - Below are the two circles sketched on the same set of axes. Once again, to find another point on the symmetrical circle, we moved [latex]\scriptsize r=9\text{ units}[/latex] horizontally to the right from the centre. The line of symmetry [latex]\scriptsize y=-x[/latex] has also been sketched to better illustrate the symmetry.
Exercise 1.2
- Write down the equation of the following circles:
- Centre [latex]\scriptsize (-3,0)[/latex] and radius [latex]\scriptsize 4\text{ units}[/latex].
- Centre [latex]\scriptsize C(-5,-1)[/latex] and passing through the point [latex]\scriptsize P(6,-2)[/latex].
- [latex]\scriptsize r=\sqrt{{11}}[/latex] and centre [latex]\scriptsize (2,-3)[/latex].
- Determine the centre and radius of the following circles:
- [latex]\scriptsize \displaystyle 5-{{x}^{2}}-6x-8y-{{y}^{2}}=0[/latex]
- [latex]\scriptsize {{x}^{2}}=21+4y-{{y}^{2}}[/latex]
- [latex]\scriptsize 12x-12y-2{{x}^{2}}-2{{y}^{2}}=24[/latex]
- A circle cuts the x-axis at [latex]\scriptsize A(-3,0)[/latex] and [latex]\scriptsize B(3,0)[/latex]. If [latex]\scriptsize r=\sqrt{{21}}[/latex], determine the possible equation(s) of the circle.
- [latex]\scriptsize P(5,6)[/latex] and [latex]\scriptsize Q(-1,-2)[/latex] are points on a circle. If [latex]\scriptsize PQ[/latex] is a diameter of the circle, determine the equation of the circle.
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- The equation of a circle centre [latex]\scriptsize (a,b)[/latex] is given by [latex]\scriptsize {{(x-a)}^{2}}+{{(y-b)}^{2}}={{r}^{2}}[/latex].
- The equation of a circle centre the origin is a special case and is given by [latex]\scriptsize {{x}^{2}}+{{y}^{2}}={{r}^{2}}[/latex].
- The circle centre the origin is symmetrical about both axes and the lines [latex]\scriptsize y=x[/latex] and [latex]\scriptsize y=-x[/latex].
Unit 1: Assessment
Suggested time to complete: 60 minutes
- Determine the equation of the circle:
- With centre the origin and a radius of [latex]\scriptsize \displaystyle \frac{7}{3}[/latex].
- With centre [latex]\scriptsize (2,-5)[/latex] and [latex]\scriptsize r=2\sqrt{{11}}[/latex].
- With centre [latex]\scriptsize C(-3,0)[/latex] passing through [latex]\scriptsize R(8,-4)[/latex].
- Passing through [latex]\scriptsize P(5q,6q)[/latex] and centre [latex]\scriptsize C(0,1)[/latex].
- Determine the value(s) of [latex]\scriptsize h[/latex] if [latex]\scriptsize (\sqrt{2},h)[/latex] is a point on the circle [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=17[/latex].
- [latex]\scriptsize P(r,s)[/latex] is a point on the circle with centre at the origin and a diameter of [latex]\scriptsize \text{70 cm}[/latex]. Determine the possible coordinates of [latex]\scriptsize P[/latex] if the value of [latex]\scriptsize r[/latex] is four times the value of [latex]\scriptsize s[/latex].
Question 4 adapted from Everything Maths Grade 12 Exercise 7-3 question 6
- [latex]\scriptsize P(-2,3)[/latex] lies on a circle with centre at [latex]\scriptsize (0,0)[/latex].
- Determine the equation of the circle.
- Sketch the circle and label point [latex]\scriptsize P[/latex].
- If [latex]\scriptsize PQ[/latex] is a diameter of the circle, determine the coordinates of [latex]\scriptsize Q[/latex].
- Calculate the length of [latex]\scriptsize PQ[/latex].
- Determine the equation of the line [latex]\scriptsize PQ[/latex].
- Determine the equation of the line perpendicular to [latex]\scriptsize PQ[/latex] and passing through the point [latex]\scriptsize P[/latex].
Question 5 adapted from Everything Maths Grade 12 Exercise 7-4 question 6
- A circle with centre [latex]\scriptsize N(4,4)[/latex] passes through the points [latex]\scriptsize K(1,6)[/latex] and [latex]\scriptsize L(6,7)[/latex].
- Draw a sketch of the circle.
- Determine the equation of the circle.
- Determine the coordinates of [latex]\scriptsize M[/latex], the midpoint of [latex]\scriptsize KL[/latex].
- Show that [latex]\scriptsize MN\bot KL[/latex].
- Determine the equation of the line [latex]\scriptsize LN[/latex].
- If [latex]\scriptsize P[/latex] is a point on the circle such that [latex]\scriptsize LP[/latex] is a diameter, determine the coordinates of [latex]\scriptsize P[/latex].
- A circle passes through the points [latex]\scriptsize A(1,2)[/latex] and [latex]\scriptsize B(-3,2)[/latex]. If its centre lies on the line [latex]\scriptsize 6x+3y=-3[/latex], determine the equation of the circle.
Question 7 adapted from Everything Maths Grade 12 Exercise 7-4 question 8
- A circle with centre [latex]\scriptsize (0,0)[/latex] passes through the point [latex]\scriptsize T(4,3)[/latex].
- Determine the equation of the circle.
- If the circle is shifted [latex]\scriptsize 2\text{ units}[/latex] to the right and [latex]\scriptsize 3\text{ units}[/latex] down, determine the new equation of the circle.
- Draw a sketch of the original circle and the shifted circle on the same system of axes.
- If the circle in 7 b. is reflected about the x-axis, what will the centre of this new circle be.
Question 8 adapted from NC(V) Mathematics Level 4 Paper 2 November 2016 question 1.5
- In the figure below two circles with a common centre [latex]\scriptsize M(-1,-2)[/latex] are shown. Radius [latex]\scriptsize MA[/latex] of the larger circle cuts the smaller circle at [latex]\scriptsize B[/latex]. Point [latex]\scriptsize A[/latex] has coordinates [latex]\scriptsize (-5,3)[/latex].
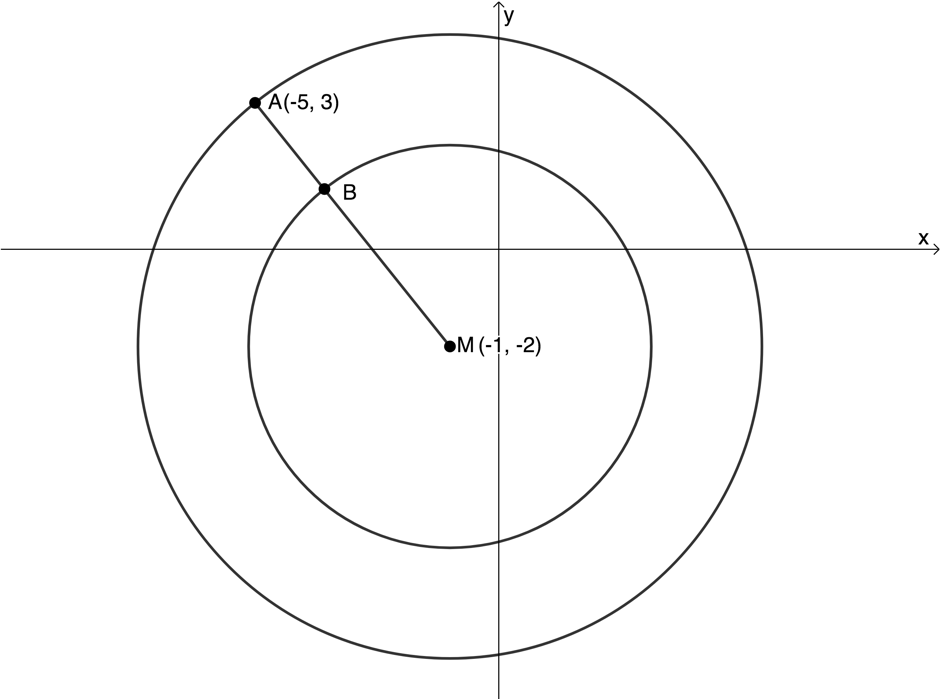
- Determine the equation of the larger circle.
- If the equation of the smaller circle is [latex]\scriptsize {{x}^{2}}+{{y}^{2}}+2x+4y-4=0[/latex], determine the length [latex]\scriptsize AB[/latex].
The full solutions are at the end of the unit.
Unit 1: Solutions
Exercise 1.1
- .
- .
- .
- .
[latex]\scriptsize \begin{align*}4{{x}^{2}}+4{{y}^{2}} & =80\\\therefore {{x}^{2}}+{{y}^{2}} & =20\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{r}^{2}} & =20\\\therefore r & =\sqrt{{20}}=2\sqrt{5}\end{align*}[/latex] - We can find a point, with coordinates that are integers, that lies on the circle to help us sketch the circle more accurately.
[latex]\scriptsize \begin{align*}20&=16+4\\&={{4}^{2}}+{{2}^{2}}\end{align*}[/latex]
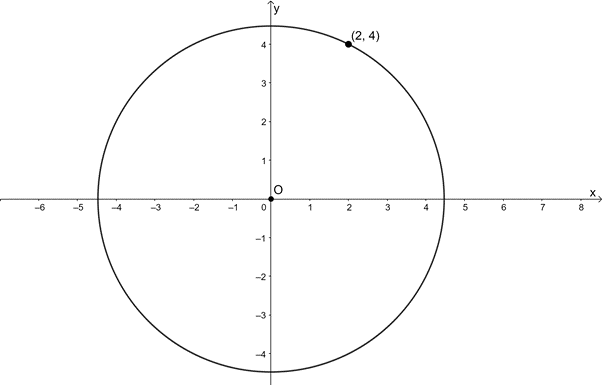
- .
- .
- [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=36[/latex]
- [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=13[/latex]
- .
[latex]\scriptsize \begin{align*}{{(-3)}^{2}}+{{(-7)}^{2}}&=9+49\\&=58\\\therefore {{x}^{2}}+{{y}^{2}} &=58\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{(2s)}^{2}}+{{(3s)}^{2}} & =4{{s}^{2}}+9{{s}^{2}}\\&=13{{s}^{2}}\\\therefore {{x}^{2}}+{{y}^{2}} & =13{{s}^{2}}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{(-5t)}^{2}}+{{(-3t)}^{2}} & =25{{t}^{2}}+9{{t}^{2}}\\&=34{{t}^{2}}\\\therefore {{x}^{2}}+{{y}^{2}} & =34{{t}^{2}}\end{align*}[/latex]
- .
[latex]\scriptsize \begin{align*}\sqrt{90}+x^2-y^2&=0\\ \therefore x^2-y^2&=-\sqrt{90}\\ \therefore y^2-x^2&=\sqrt{90}\end{align*}[/latex]
This is not the equation of a circle with centre the origin. - [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=50[/latex] and [latex]\scriptsize x=3y[/latex]. Therefore:
[latex]\scriptsize \begin{align*}{{(3y)}^{2}}+{{y}^{2}} & =50\\\therefore 9{{y}^{2}}+{{y}^{2}} & =50\\\therefore 10{{y}^{2}} & =50\\\therefore {{y}^{2}} & =5\\\therefore y & =\pm \sqrt{5}\end{align*}[/latex]
Substitute [latex]\scriptsize y=+\sqrt{5}[/latex]:
[latex]\scriptsize \begin{align*}{{x}^{2}}+{{\left( {\sqrt{5}} \right)}^{2}} & =50\\\therefore {{x}^{2}}+5 & =50\\\therefore {{x}^{2}} & =45\\\therefore x & =\pm \sqrt{{45}}\\ & =\pm 3\sqrt{5}\end{align*}[/latex]
Because the circle is symmetrical about the x-axis, we will get the same result substituting [latex]\scriptsize y=-\sqrt{5}[/latex]. Therefore, there are four possible points.
[latex]\scriptsize (3\sqrt{5},\sqrt{5})[/latex], [latex]\scriptsize (-3\sqrt{5},-\sqrt{5})[/latex], [latex]\scriptsize (-3\sqrt{5},\sqrt{5})[/latex] and [latex]\scriptsize (3\sqrt{5},-\sqrt{5})[/latex]
Exercise 1.2
- .
- [latex]\scriptsize {{(x+3)}^{2}}+{{y}^{2}}=16[/latex]
- Equation is of the form [latex]\scriptsize {{(x+5)}^{2}}+{{(y+1)}^{2}}={{r}^{2}}[/latex]. Length of [latex]\scriptsize CP[/latex] is the radius.
[latex]\scriptsize \begin{align*}{{d}_{{CP}}}&=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}\\&=\sqrt{{{{{(-5-6)}}^{2}}+{{{(-1-(-2))}}^{2}}}}\\&=\sqrt{{{{{(-11)}}^{2}}+{{1}^{2}}}}\\&=\sqrt{{121+1}}\\&=\sqrt{{122}}\end{align*}[/latex]
The equation is [latex]\scriptsize {{(x+5)}^{2}}+{{(y+1)}^{2}}=122[/latex]. - [latex]\scriptsize {{(x-2)}^{2}}+{{(y+3)}^{2}}=11[/latex]
- Determine the centre and radius of the following circles:
- .
[latex]\scriptsize \begin{align*}5-x^2-6x-8y-y^2&=0\\ x^2+6x+y^2+8y&=5&&\text{Complete the squares}\\ \therefore x^2+6x+9+y^2+8y+16&=5+9+16\\ \therefore (x+3)^2+(y+4)^2&=30\end{align*}[/latex]
The centre is [latex]\scriptsize (-3,-4)[/latex], the radius is [latex]\scriptsize \sqrt{{30}}[/latex]. - .
[latex]\scriptsize \begin{align*}x^2&=21+4y-y^2\\ x^2+y^2-4y&=21&&\text{Complete the square}\\ \therefore x^2+y^2-4y-+4&=21+4\\ \therefore x^2+(y-2)^2&=25\end{align*}[/latex]
The centre is [latex]\scriptsize (0,2)[/latex], the radius is [latex]\scriptsize 5[/latex]. - .
[latex]\scriptsize \begin{align*}12x-12y-2{{x}^{2}}-2{{y}^{2}} & =24\\\therefore 2{{x}^{2}}-12x+2{{y}^{2}}+12y & =24\\\therefore {{x}^{2}}-6x+{{y}^{2}}+6y & =12\quad \text{Complete the squares}\\\therefore {{x}^{2}}-6x+9+{{y}^{2}}+6y+9 & =12+9+9\\\therefore {{(x-3)}^{2}}+{{(y+3)}^{2}} & =30\end{align*}[/latex]
The centre is [latex]\scriptsize (3,-3)[/latex], the radius is [latex]\scriptsize \sqrt{{30}}[/latex].
- .
- The equation of the circle is [latex]\scriptsize {{(x-a)}^{2}}+{{(y-b)}^{2}}=21[/latex]. [latex]\scriptsize A(-3,0)[/latex] and [latex]\scriptsize B(3,0)[/latex] lie on the circle.
Substitute [latex]\scriptsize A(-3,0)[/latex]:
[latex]\scriptsize \begin{align*}{{(-3-a)}^{2}}+{{(0-b)}^{2}} & =21\\\therefore 9+6a+{{a}^{2}}+{{b}^{2}} & =21\\\therefore {{a}^{2}}+6a+9 & =21-{{b}^{2}}\quad \quad (1)\end{align*}[/latex]
Substitute [latex]\scriptsize B(3,0)[/latex]:
[latex]\scriptsize \begin{align*}{{(3-a)}^{2}}+{{(0-b)}^{2}} & =21\\\therefore 9-6a+{{a}^{2}}+{{b}^{2}} & =21\\\therefore {{a}^{2}}-6a+9 & =21-{{b}^{2}}\quad \quad (2)\end{align*}[/latex]
Set [latex]\scriptsize (1)=(2)[/latex]:
[latex]\scriptsize \begin{align*}{{a}^{2}}+6a+9 & ={{a}^{2}}-6a+9\\\therefore 12a & =0\\\therefore a & =0\end{align*}[/latex]
Substitute [latex]\scriptsize a=0[/latex] into [latex]\scriptsize (1)[/latex]:
[latex]\scriptsize \begin{align*}9 & =21-{{b}^{2}}\\\therefore {{b}^{2}} & =12\\\therefore b & =\pm \sqrt{{12}}\\\therefore b & =\pm 2\sqrt{3}\end{align*}[/latex]
The possible equations of the circle are [latex]\scriptsize {{x}^{2}}+{{\left( {y-2\sqrt{3}} \right)}^{2}}=21[/latex] or [latex]\scriptsize {{x}^{2}}+{{\left( {y+2\sqrt{3}} \right)}^{2}}=21[/latex]. - If [latex]\scriptsize PQ[/latex] is a diameter of the circle, then the midpoint of [latex]\scriptsize PQ[/latex] is the centre.
[latex]\scriptsize \begin{align*}\text{midpoin}{{\text{t}}_{{PQ}}}&=\left( {\displaystyle \frac{{{{x}_{1}}+{{x}_{2}}}}{2},\displaystyle \frac{{{{y}_{1}}+{{y}_{2}}}}{2}} \right)\\&=\left( {\displaystyle \frac{{5-1}}{2},\displaystyle \frac{{6-2}}{2}} \right)\\&=(2,2)\end{align*}[/latex]
The radius of the circle is the distance from the centre, [latex]\scriptsize C[/latex], to either [latex]\scriptsize P[/latex] or [latex]\scriptsize Q[/latex].
[latex]\scriptsize \begin{align*}{{d}_{{CP}}}&=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}\\&=\sqrt{{{{{(5-2)}}^{2}}+{{{(6-2)}}^{2}}}}\\&=\sqrt{{{{3}^{2}}+{{4}^{2}}}}\\&=\sqrt{{9+16}}\\&=\sqrt{{25}}\\&=5\end{align*}[/latex]
Therefore, the equation of the circle is [latex]\scriptsize {{(x-2)}^{2}}+{{(y-2)}^{2}}=25[/latex].
Unit 1: Assessment
- .
- [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=\displaystyle \frac{{49}}{9}[/latex]
- [latex]\scriptsize {{(x-2)}^{2}}+{{(y+5)}^{2}}=44[/latex]
- .
[latex]\scriptsize \begin{align*}r&={{d}_{{CR}}}=\sqrt{{{{{({{x}_{1}}-{{x}_{2}})}}^{2}}+{{{({{y}_{1}}-{{y}_{2}})}}^{2}}}}\\&=\sqrt{{{{{(-3-8)}}^{2}}+{{{(0-(-4))}}^{2}}}}\\&=\sqrt{{{{{(-11)}}^{2}}+{{4}^{2}}}}\\&=\sqrt{{121+16}}\\&=\sqrt{{137}}\end{align*}[/latex]
The equation is [latex]\scriptsize {{(x+3)}^{2}}+{{y}^{2}}=137[/latex]. - .
[latex]\scriptsize \begin{align*}r&={{d}_{{CP}}}=\sqrt{{{{{({{x}_{1}}-{{x}_{2}})}}^{2}}+{{{({{y}_{1}}-{{y}_{2}})}}^{2}}}}\\&=\sqrt{{{{{(5q-0)}}^{2}}+{{{(6q-1)}}^{2}}}}\\&=\sqrt{{25{{q}^{2}}+36{{q}^{2}}-12q+1}}\\&=\sqrt{{61{{q}^{2}}-12q+1}}\end{align*}[/latex]
The equation is [latex]\scriptsize {{x}^{2}}+{{(y-1)}^{2}}=61{{q}^{2}}-12q+1[/latex].
- Substitute in [latex]\scriptsize (\sqrt{2},h)[/latex]:
[latex]\scriptsize \begin{align*}{{\left( {\sqrt{2}} \right)}^{2}}+{{h}^{2}} & =17\\\therefore 2+{{h}^{2}} & =17\\\therefore {{h}^{2}} & =15\\\therefore h & =\pm \sqrt{{15}}\end{align*}[/latex] - Diameter is [latex]\scriptsize \text{70 cm}[/latex]. Therefore, radius is [latex]\scriptsize \text{35 cm}[/latex].
[latex]\scriptsize r=4s[/latex]. Substitute [latex]\scriptsize x=r=4s[/latex] and [latex]\scriptsize y=s[/latex] into [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=1\ 225[/latex].
[latex]\scriptsize \begin{align*}{{(4s)}^{2}}+{{(s)}^{2}} & =1\ 225\\\therefore 16{{s}^{2}}+{{s}^{2}} & =1\ 225\\\therefore 17{{s}^{2}} & =1\ 225\\\therefore {{s}^{2}} & =\displaystyle \frac{{1\ 225}}{{17}}\\\therefore s & =\pm \displaystyle \frac{{35}}{{\sqrt{{17}}}}\end{align*}[/latex]
Therefore:
[latex]\scriptsize \begin{align*}r & =4\times \left( {\pm \displaystyle \frac{{35}}{{\sqrt{{17}}}}} \right)\\ & =\pm \displaystyle \frac{{140}}{{\sqrt{{17}}}}\end{align*}[/latex]
The possible coordinates of [latex]\scriptsize P(r,s)[/latex] are [latex]\scriptsize \left( {\pm \displaystyle \frac{{140}}{{\sqrt{{17}}}},\pm \displaystyle \frac{{35}}{{\sqrt{{17}}}}} \right)[/latex]. - .
- .
[latex]\scriptsize \begin{align*}{{r}^{2}}&={{(-2)}^{2}}+{{3}^{2}}\\&=4+9\\&=13\end{align*}[/latex]
The equation of the circle is [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=13[/latex]. - .
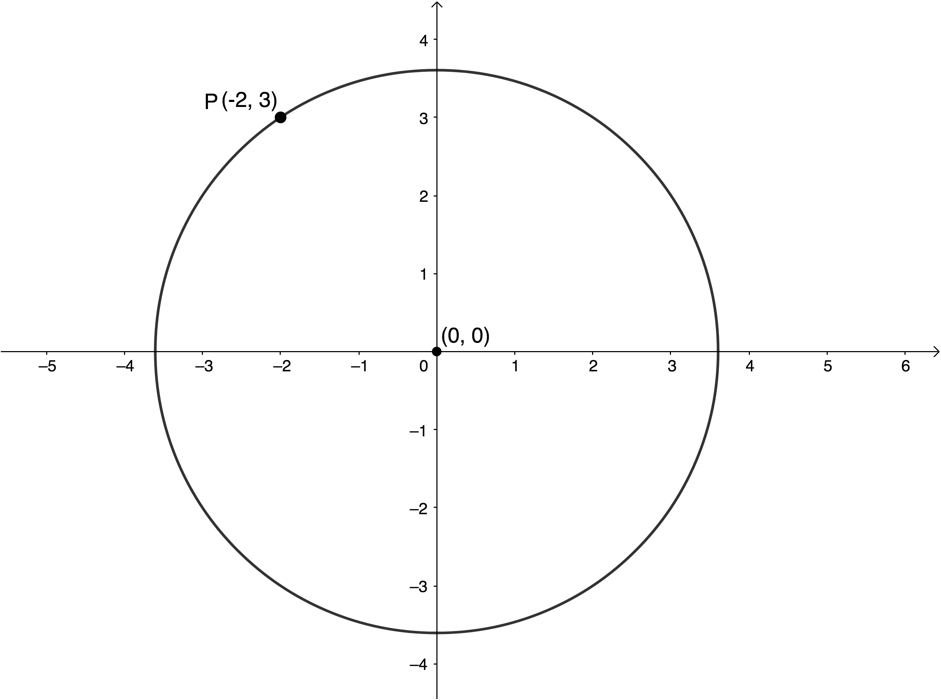
- If [latex]\scriptsize PQ[/latex] is a diameter then [latex]\scriptsize P[/latex] and [latex]\scriptsize Q[/latex] are symmetrical about the line [latex]\scriptsize y=x[/latex]. Therefore [latex]\scriptsize Q(3,-2)[/latex].
- .
[latex]\scriptsize \begin{align*}{{d}_{{PQ}}}&=\sqrt{{{{{({{x}_{1}}-{{x}_{2}})}}^{2}}+{{{({{y}_{1}}-{{y}_{2}})}}^{2}}}}\\&=\sqrt{{{{{(-2-3)}}^{2}}+{{{(3-(-2))}}^{2}}}}\\&=\sqrt{{{{{(-5)}}^{2}}+{{5}^{2}}}}\\&=\sqrt{{50}}\\&=5\sqrt{2}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{m}_{{PQ}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{3-(-2)}}{{-2-3}}\\&=-\displaystyle \frac{5}{5}\\&=-1\end{align*}[/latex]
[latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-3 & =-1\left( {x-(-2)} \right)\\\therefore y-3 & =-(x+2)\\\therefore y-3 & =-x-2\\\therefore y & =-x+1\end{align*}[/latex] - The gradient of the line perpendicular to [latex]\scriptsize PQ[/latex] is [latex]\scriptsize m=1[/latex].
[latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-3 & =1\left( {x-(-2)} \right)\\\therefore y-3 & =(x+2)\\\therefore y-3 & =x+2\\\therefore y & =x+5\end{align*}[/latex]
- .
- .
- .
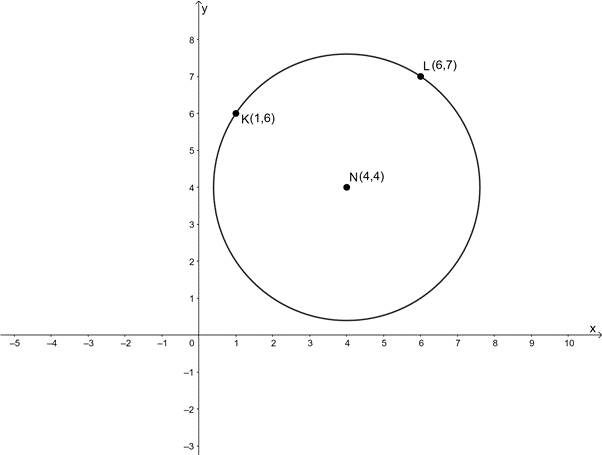
- .
[latex]\scriptsize \begin{align*}r={{d}_{{NK}}}&=\sqrt{{{{{({{x}_{1}}-{{x}_{2}})}}^{2}}+{{{({{y}_{1}}-{{y}_{2}})}}^{2}}}}\\&=\sqrt{{{{{(4-1)}}^{2}}+{{{(4-6)}}^{2}}}}\\&=\sqrt{{{{{(-3)}}^{2}}+{{{(-2)}}^{2}}}}\\&=\sqrt{{9+4}}\\&=\sqrt{{13}}\end{align*}[/latex]
The equation is [latex]\scriptsize {{(x-4)}^{2}}+{{(y-4)}^{2}}=13[/latex]. - .
[latex]\scriptsize \begin{align*}\text{M=midpoin}{{\text{t}}_{{KL}}}&=\left( {\displaystyle \frac{{{{x}_{1}}+{{x}_{2}}}}{2},\displaystyle \frac{{{{y}_{1}}+{{y}_{2}}}}{2}} \right)\\&=\left( {\displaystyle \frac{{1+6}}{2},\displaystyle \frac{{6+7}}{2}} \right)\\&=(\displaystyle \frac{7}{2},\displaystyle \frac{{13}}{2})\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{m}_{{MN}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{\displaystyle \frac{{13}}{2}-4}}{{\displaystyle \frac{7}{2}-4}}\\&=\displaystyle \frac{{\displaystyle \frac{5}{2}}}{{-\displaystyle \frac{1}{2}}}\\&=\displaystyle \frac{5}{2}\times \left( {-\displaystyle \frac{2}{1}} \right)=-5\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{m}_{{KL}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{7-6}}{{6-1}}\\&=\displaystyle \frac{1}{5}\end{align*}[/latex]
[latex]\scriptsize {{m}_{{MN}}}\times {{m}_{{KL}}}=-1[/latex]. Therefore, [latex]\scriptsize MN\bot KL[/latex]. - Equation of LN:
[latex]\scriptsize \begin{align*}{{m}_{{LN}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{7-4}}{{6-4}}\\&=\displaystyle \frac{3}{2}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-4 & =\displaystyle \frac{3}{2}(x-4)\\\therefore y-4 & =\displaystyle \frac{3}{2}x-6\\\therefore y & =\displaystyle \frac{3}{2}x-2\end{align*}[/latex] - Since [latex]\scriptsize N[/latex] is the centre of the circle passing through point [latex]\scriptsize L[/latex], [latex]\scriptsize LN[/latex] is a radius. Given that [latex]\scriptsize LP[/latex] is a diameter, [latex]\scriptsize L[/latex], [latex]\scriptsize N[/latex] and [latex]\scriptsize P[/latex] lie on the same straight line. Equation of [latex]\scriptsize LP[/latex]is thus:
[latex]\scriptsize y =\displaystyle \frac{3}{2}x-2\quad \quad (1)[/latex]
[latex]\scriptsize (x-4)^2+(y-4)^2=13\quad \quad (2)[/latex]
Substitute [latex]\scriptsize (1)[/latex] into [latex]\scriptsize (2)[/latex]:
[latex]\scriptsize \begin{align*}{{(x-4)}^{2}}+{{\left( {\left( {\displaystyle \frac{3}{2}x-2} \right)-4} \right)}^{2}} & =13\\\therefore {{x}^{2}}-8x+16+{{\left( {\displaystyle \frac{3}{2}x-6} \right)}^{2}} & =13\\\therefore {{x}^{2}}-8x+16+\displaystyle \frac{9}{4}{{x}^{2}}-18x+36 & =13\\\therefore \displaystyle \frac{{13}}{4}{{x}^{2}}-26x+39 & =0\\\therefore 13{{x}^{2}}-104x+156 & =0\\\therefore {{x}^{2}}-8x+12 & =0\\\therefore (x-2)(x-6) & =0\\\therefore x=2\text{ } & \text{or }x=6\end{align*}[/latex]
[latex]\scriptsize x=6[/latex] is the x-coordinate of [latex]\scriptsize L[/latex]. Therefore [latex]\scriptsize x=2[/latex] is the x-coordinate of [latex]\scriptsize P[/latex].
Substitute [latex]\scriptsize x=2[/latex] into [latex]\scriptsize (1)[/latex]:
[latex]\scriptsize \begin{align*}y & =\displaystyle \frac{3}{2}(2)-2\\ & =1\end{align*}[/latex]
[latex]\scriptsize P(2,1)[/latex]
- .
- .
[latex]\scriptsize \begin{align*}6x+3y&=-3\\\therefore 3y & =-6x-3\\\therefore y & =-2x-1\end{align*}[/latex]
Every point on this line has coordinates [latex]\scriptsize \left( {x,-2x-1} \right)[/latex]. If the centre is [latex]\scriptsize C[/latex], [latex]\scriptsize {{d}_{{AC}}}={{d}_{{BC}}}[/latex].
[latex]\scriptsize \begin{align*}{{d}_{{AC}}}&=\sqrt{{{{{({{x}_{1}}-{{x}_{2}})}}^{2}}+{{{({{y}_{1}}-{{y}_{2}})}}^{2}}}}\\&=\sqrt{{{{{(1-x)}}^{2}}+{{{\left( {2-\left( {-2x-1} \right)} \right)}}^{2}}}}\\&=\sqrt{{1-2x+{{x}^{2}}+{{{\left( {2x+3} \right)}}^{2}}}}\\&=\sqrt{{1-2x+{{x}^{2}}+4{{x}^{2}}+12x+9}}\\&=\sqrt{{5{{x}^{2}}+10x+10}}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{d}_{{BC}}}&=\sqrt{{{{{({{x}_{1}}-{{x}_{2}})}}^{2}}+{{{({{y}_{1}}-{{y}_{2}})}}^{2}}}}\\&=\sqrt{{{{{(-3-x)}}^{2}}+{{{\left( {2-\left( {-2x-1} \right)} \right)}}^{2}}}}\\&=\sqrt{{9+6x+{{x}^{2}}+{{{\left( {2x+3} \right)}}^{2}}}}\\&=\sqrt{{9+6x+{{x}^{2}}+4{{x}^{2}}+12x+9}}\\&=\sqrt{{5{{x}^{2}}+18x+18}}\end{align*}[/latex]
But [latex]\scriptsize {{d}_{{AC}}}={{d}_{{BC}}}[/latex]. Therefore:
[latex]\scriptsize \begin{align*}\sqrt{{5{{x}^{2}}+10x+10}} & =\sqrt{{5{{x}^{2}}+18x+18}}\\\therefore 5{{x}^{2}}+10x+10 & =5{{x}^{2}}+18x+18\\\therefore 10x+10 & =18x+18\\\therefore 8x & =-8\\\therefore x & =-1\end{align*}[/latex]
[latex]\scriptsize \begin{align*}y & =-2x-1\\&=-2(-1)-1\\&=1\end{align*}[/latex]
The centre of the circle is the point [latex]\scriptsize (-1,1)[/latex].
[latex]\scriptsize \begin{align*}r&={{d}_{{AC}}}=\sqrt{{{{{({{x}_{1}}-{{x}_{2}})}}^{2}}+{{{({{y}_{1}}-{{y}_{2}})}}^{2}}}}\\&=\sqrt{{{{{\left( {1-(-1)} \right)}}^{2}}+{{{\left( {2-1} \right)}}^{2}}}}\\&=\sqrt{{4+1}}\\&=\sqrt{5}\end{align*}[/latex]
The equation of the circle is [latex]\scriptsize {{(x+1)}^{2}}+{{(y-1)}^{2}}=5[/latex] - .
- .
[latex]\scriptsize \begin{align*}{{r}^{2}}&={{x}^{2}}+{{y}^{2}}\\&={{4}^{2}}+{{3}^{2}}\\&=16+9\\&=25\end{align*}[/latex]
The equation of the circle is [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=25[/latex]. - [latex]\scriptsize {{(x-2)}^{2}}+{{(y+3)}^{2}}=25[/latex]
- .
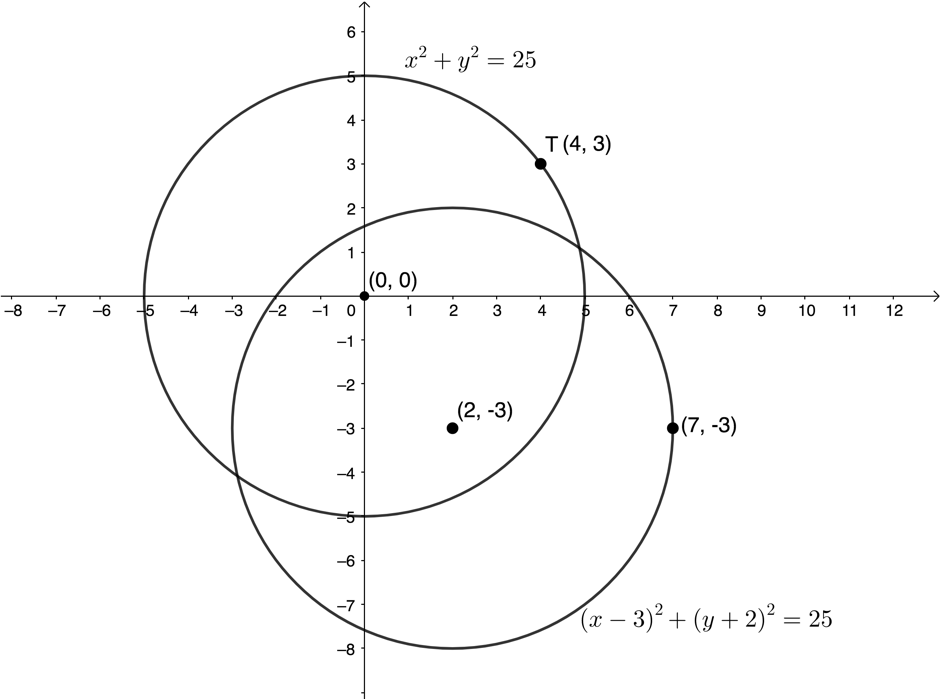
- The centre of new circle will be [latex]\scriptsize (2,3)[/latex].
- .
- .
- The equation has the form [latex]\scriptsize {{(x+1)}^{2}}+{{(y+2)}^{2}}={{r}^{2}}[/latex].
[latex]\scriptsize \begin{align*}r&={{d}_{{MA}}}=\sqrt{{{{{({{x}_{1}}-{{x}_{2}})}}^{2}}+{{{({{y}_{1}}-{{y}_{2}})}}^{2}}}}\\&=\sqrt{{{{{\left( {-1-(-5)} \right)}}^{2}}+{{{\left( {-2-3} \right)}}^{2}}}}\\&=\sqrt{{{{4}^{2}}+{{{(-5)}}^{2}}}}\\&=\sqrt{{16+25}}\\&=\sqrt{{41}}\end{align*}[/latex]
The equation is [latex]\scriptsize {{(x+1)}^{2}}+{{(y+2)}^{2}}=41[/latex]. - .
[latex]\scriptsize \displaystyle \begin{align*}{{x}^{2}}+{{y}^{2}}+2x+4y-4 & =0\\\therefore {{x}^{2}}+2x+{{y}^{2}}+4y & =4\\\therefore {{x}^{2}}+2x+1+{{y}^{2}}+4y+4 & =4+1+4\\\therefore {{(x+1)}^{2}}+{{(y+2)}^{2}} & =9\end{align*}[/latex]
Therefore, radius of the smaller circle is [latex]\scriptsize 3[/latex].
[latex]\scriptsize \begin{align*}AB&=AM-BM\\&=\sqrt{{41}}-3\end{align*}[/latex]
- The equation has the form [latex]\scriptsize {{(x+1)}^{2}}+{{(y+2)}^{2}}={{r}^{2}}[/latex].
Media Attributions
- figure1 © DHET is licensed under a CC BY (Attribution) license
- figure7 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- activity1.1 A1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- activity1.1 A4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example1.1 A2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example1.2 A1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- symmetry © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q4e © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure6 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure7 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure8 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example1.3 A2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example1.5 A2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example1.5 A4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q8 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 A1b © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 A2b © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 A3b © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment A4b © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment A5a © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment A7d © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license