Unit outcomes

By the end of this unit you will be able to:

• Find the area under a curve between two points and bound by the x-axis.

What you should know

Before you start this unit, make sure you can:

• Sketch cubic functions.
• Apply the rules of integration.
• Find the definite integral.
• Find the indefinite integral.

Try these questions to make sure you are ready for this unit:

1. Find: [latex]\scriptsize \int{{\left( {\displaystyle \frac{{4-4x+{{x}^{2}}}}{{x-2}}} \right)}}dx[/latex]
2. Calculate: [latex]\scriptsize \int_{{-1}}^{2}{{({{x}^{3}}-2{{x}^{2}}-4x+10)dx}}[/latex]
3. Evaluate: [latex]\scriptsize \int_{0}^{\pi }{{\cos 2xdx}}[/latex]

Solutions

1. .
   [latex]\scriptsize \displaystyle \begin{align*}\int{{\left( {\displaystyle \frac{{4-4x+{{x}^{2}}}}{{x-2}}} \right)}}dx&=\int{{\left( {\displaystyle \frac{{(2-x)(2-x)}}{{-(2-x)}}} \right)}}dx\\&=\int{{\left( {-(2-x)} \right)dx}}\\&=\int{{(x-2}})dx\\&=\displaystyle \frac{{{{x}^{2}}}}{2}-2x+c\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}\int_{{-1}}^{2}{{({{x}^{3}}-2{{x}^{2}}-4x+10)dx}}&=\left. {\displaystyle \frac{{{{x}^{4}}}}{4}-\displaystyle \frac{{2{{x}^{3}}}}{3}-\displaystyle \frac{{4{{x}^{2}}}}{2}+10x} \right|_{{-1}}^{2}\\&=\left[ {\displaystyle \frac{{{{2}^{4}}}}{4}-\displaystyle \frac{{2{{{(2)}}^{3}}}}{3}-2{{{(2)}}^{2}}+10(2)} \right]-\left[ {\displaystyle \frac{{{{{(-1)}}^{4}}}}{4}-\displaystyle \frac{{2{{{(-1)}}^{3}}}}{3}-2{{{(-1)}}^{2}}+10(-1)} \right]\\&=\displaystyle \frac{{32}}{3}-(-\displaystyle \frac{{133}}{{12}})\\&=\displaystyle \frac{{87}}{4}\\&=21.75\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*}\int_{0}^{\pi }{{\cos 2xdx}}&=\left. {\displaystyle \frac{{\sin 2x}}{2}} \right|_{0}^{\pi }\\&=(\displaystyle \frac{{\sin 2\pi }}{2})-(\displaystyle \frac{{\sin 2\left( 0 \right)}}{2})\\&=0\end{align*}[/latex]

Introduction

We have seen in units [latex]\scriptsize 1[/latex] and [latex]\scriptsize 2[/latex] of this subject outcome that we can find the area between a curve, the x-axis, and specific ordinates, by using integration. In this unit we will look at how to apply this idea in more complicated situations.

The area between a curve and the x-axis

Let us do an activity to revise how to find an area of a segment under a curve.

Activity 3.1: Find the areas of the segments contained between the curve y=x(x-1)(x-2) and the x-axis

Time required: 25 minutes

What you need:

• a pen and paper

What to do:

1. Sketch the graph of [latex]\scriptsize y=x(x-1)(x-2)[/latex].
2. Write down the x-intercepts of the graph.
3. Mark the areas between the curve and the x-axis as [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex].
4. Write down the position of area [latex]\scriptsize A[/latex] in relation to the x-axis.
5. Write down the position of area [latex]\scriptsize B[/latex] in relation to the x-axis.
6. Decide if the positions of [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex] make any difference to the area.
7. Calculate the definite integral of [latex]\scriptsize x(x-1)(x-2)[/latex] between the points [latex]\scriptsize (0,0)[/latex]and [latex]\scriptsize (1,0)[/latex].
8. State what the value you have just calculated represents.
9. Calculate the definite integral of [latex]\scriptsize x(x-1)(x-2)[/latex] between the points [latex]\scriptsize (1,0)[/latex]and [latex]\scriptsize (2,0)[/latex].
10. State what the value you have just calculated represents and why this value is negative.
11. Hence, find the total area contained between the curve and the x-axis.
12. Calculate the definite integral of [latex]\scriptsize x(x-1)(x-2)[/latex] between the points [latex]\scriptsize (0,0)[/latex] and [latex]\scriptsize (2,0)[/latex]. Compare this answer to the answer you found for the areas of [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex] previously.

What did you find?

• Compare the graph you drew to [latex]\scriptsize y=x(x-1)(x-2)[/latex] drawn here. Did you get the same shape of graph?
  
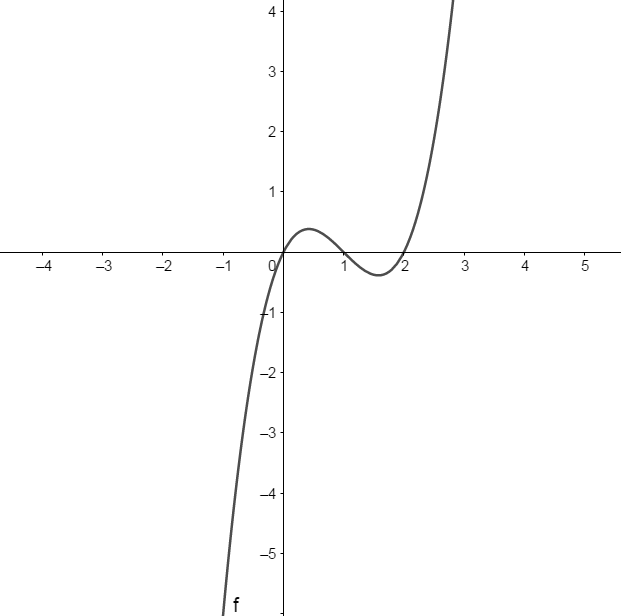
• The x-intercepts, which are calculated by letting [latex]\scriptsize y=0[/latex], are [latex]\scriptsize (0,0),(1,0)[/latex] and [latex]\scriptsize (2,0)[/latex].
• [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex] shown on the graph represent the areas between the curve and the x-axis.
  
• We notice that area [latex]\scriptsize A[/latex] lies above the x-axis and area [latex]\scriptsize B[/latex] lies below the x-axis. In previous units we have only calculated areas using integration when the area of the curve is above the x-axis. Does the position of the curve make any difference to the area? Let us calculate the definite integrals over each interval separately so we can see what happens.
• We know that the area [latex]\scriptsize A[/latex] is given by the integral from [latex]\scriptsize x=0[/latex] to [latex]\scriptsize x=1[/latex] of the curve [latex]\scriptsize y=x(x-1)(x-2)={{x}^{3}}-3{{x}^{2}}+2x[/latex]. Therefore:
  [latex]\scriptsize \displaystyle \begin{align*}A&=\int_{0}^{1}{{({{x}^{3}}-3{{x}^{2}}+2x}})dx\\&=\left. {\displaystyle \frac{{{{x}^{4}}}}{4}-\displaystyle \frac{{3{{x}^{3}}}}{3}+\displaystyle \frac{{2{{x}^{2}}}}{2}} \right|_{0}^{1}\\&=\left. {\displaystyle \frac{{{{x}^{4}}}}{4}-{{x}^{3}}+{{x}^{2}}} \right|_{0}^{1}\\&=\left[ {\displaystyle \frac{1}{4}-1+1} \right]-\left[ {\displaystyle \frac{0}{4}-0+0} \right]\\&=\displaystyle \frac{1}{4}\end{align*}[/latex]
• Area [latex]\scriptsize B[/latex] is given by a similar integral, but now the limits of integration are from [latex]\scriptsize x=1[/latex] to [latex]\scriptsize x=2[/latex].
  [latex]\scriptsize \displaystyle \begin{align*}B&=\int_{1}^{2}{{({{x}^{3}}-3{{x}^{2}}+2x}})dx\\&=\left. {\displaystyle \frac{{{{x}^{4}}}}{4}-{{x}^{3}}+{{x}^{2}}} \right|_{1}^{2}\\&=\left[ {\displaystyle \frac{{16}}{4}-8+4} \right]-\left[ {\displaystyle \frac{1}{4}-1+1} \right]\\&=-\displaystyle \frac{1}{4}\end{align*}[/latex]
• We see that the two integrals have the same magnitude but area [latex]\scriptsize A[/latex] is above the x-axis and area [latex]\scriptsize B[/latex] is below the x-axis, and the sign of the value [latex]\scriptsize B[/latex] is negative. The actual or absolute value of the area [latex]\scriptsize B[/latex] is [latex]\scriptsize \displaystyle \displaystyle \frac{1}{4}[/latex], so why does our calculation give a negative answer? In unit 1: Introduction to integration, when we summed all the tiny rectangles, we used [latex]\scriptsize \sum{{f({{x}_{i}})\Delta x}}[/latex]. Recall that [latex]\scriptsize \Delta x[/latex] was defined as a small positive increment in [latex]\scriptsize x[/latex] but [latex]\scriptsize f({{x}_{i}})[/latex] was simply the y-value at the corresponding x-value. Clearly this y-value will be negative if the curve is below the x-axis, so in this case, the quantity [latex]\scriptsize f({{x}_{i}})\Delta x[/latex] gives a negative answer as this part of the curve is fully below the x-axis. The negative just tells us that the area lies below the curve, but the actual measurement of the area will be [latex]\scriptsize \displaystyle \frac{1}{4}[/latex].
• Area is always positive, but a definite integral can still produce a negative number (a net signed area, which is the area above the x-axis less the area below the x-axis). For example, if this were a profit function, a negative number indicates the company is operating at a loss over the given interval.
• To find the total area enclosed by the curve and the x-axis we add the area of[latex]\scriptsize A[/latex], [latex]\scriptsize \displaystyle \frac{1}{4}[/latex], to the absolute value of the area [latex]\scriptsize B[/latex], which is also [latex]\scriptsize \displaystyle \frac{1}{4}[/latex]. Thus the total area enclosed by the curve and the x-axis is [latex]\scriptsize \displaystyle \frac{1}{2}[/latex].
• If we had decided to find the total area by calculating the definite integral of [latex]\scriptsize x(x-1)(x-2)[/latex] between the points [latex]\scriptsize (0,0)[/latex] and [latex]\scriptsize (2,0)[/latex], without drawing a sketch, what answer would we get?
  .
  We would find:
  [latex]\scriptsize \displaystyle \begin{align*}Area&=\int_{0}^{2}{{({{x}^{3}}-3{{x}^{2}}+2x}})dx\\&=\left. {\displaystyle \frac{{{{x}^{4}}}}{4}-{{x}^{3}}+{{x}^{2}}} \right|_{0}^{2}\\&=\left[ {\displaystyle \frac{{16}}{4}-8+4} \right]-\left[ {\displaystyle \frac{0}{4}-0+0} \right]\\&=0\end{align*}[/latex]
  So according to this calculation, the area enclosed by the curve and the x-axis is zero. But, we know that this is not the case. We have a sketch to prove it. Clearly what has happened is that the values of the two areas with different signs have been added together in the process of integration, and they have cancelled each other out. A picture can often tell us more about a function than the results of computations.
  .
  Thus, the value of the integral evaluated between two x-values is not necessarily the value of the area between the curve, the x-axis and the two ordinates. So, we must be very careful when calculating areas to avoid this particular trap. The best way to find the area is to always draw a sketch of the curve over the required range of values of [latex]\scriptsize \displaystyle x[/latex] .

Take note!

When calculating the area between a curve and the x-axis, you should do separate calculations for the parts of the curve above the axis, and the parts of the curve below the axis. The integral for a part of the curve below the axis gives a negative area for that part. It is very helpful to draw a sketch of the curve for the required range of x-values, in order to see how many separate calculations will be needed.

There are times when you will be given a sketch and required to calculate the area based on the diagram. The next example goes through this type of question and shows two methods to find the area when one segment is below the curve and the other above.

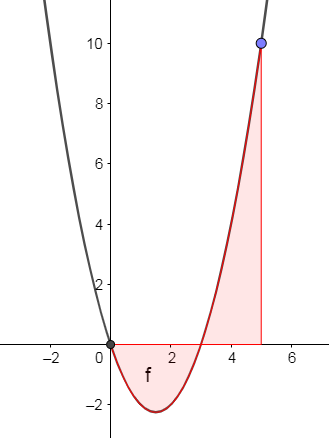
Example 3.1

Find the area between the curve [latex]\scriptsize y=x(x-3)[/latex] from [latex]\scriptsize x=0[/latex] to [latex]\scriptsize x=5[/latex].

 

Solution

Method 1:

From the graph, we can see that we need to calculate the area between the curve, the x-axis and [latex]\scriptsize \displaystyle x=0[/latex] and [latex]\scriptsize \displaystyle x=3[/latex] first, and that we should expect this integral to give a negative answer because the area is completely below the x-axis.

[latex]\scriptsize \displaystyle \begin{align*}\int_{0}^{3}{{({{x}^{2}}-3x)}}dx&=\left. {\displaystyle \frac{{{{x}^{3}}}}{3}-\displaystyle \frac{{3{{x}^{2}}}}{2}} \right|_{0}^{3}\\&=\left[ {\displaystyle \frac{{27}}{3}-\displaystyle \frac{{3(9)}}{2}} \right]-\left[ {\displaystyle \frac{0}{3}-\displaystyle \frac{{3(0)}}{3}} \right]\\&=-4\tfrac{1}{2}\end{align*}[/latex]

Next, we need to calculate the area between the curve, the x-axis, and [latex]\scriptsize \displaystyle x=3[/latex] and [latex]\scriptsize \displaystyle x=5[/latex].

[latex]\scriptsize \displaystyle \begin{align*}\int_{3}^{5}{{({{x}^{2}}-3x)}}dx&=\left. {\displaystyle \frac{{{{x}^{3}}}}{3}-\displaystyle \frac{{3{{x}^{2}}}}{2}} \right|_{3}^{5}\\&=\left[ {\displaystyle \frac{{125}}{3}-\displaystyle \frac{{3(25)}}{2}} \right]-\left[ {\displaystyle \frac{{27}}{3}-\displaystyle \frac{{3(9)}}{3}} \right]\\&=8\tfrac{2}{3}\end{align*}[/latex]

So, the total area is [latex]\scriptsize \displaystyle 4\tfrac{1}{2}+8\tfrac{2}{3}=13\tfrac{1}{6}[/latex].

Method 2:

Another way we can arrive at the same answer is to represent the area below the curve using a negative sign in front of the integral.

[latex]\scriptsize \displaystyle -\int_{0}^{3}{{({{x}^{2}}-3x)}}dx+\int_{3}^{5}{{({{x}^{2}}-3x)}}dx[/latex]

[latex]\scriptsize \displaystyle \begin{align*}-\int_{0}^{3}{{({{x}^{2}}-3x)}}dx+\int_{3}^{5}{{({{x}^{2}}-3x)}}dx&=\left. {-(\displaystyle \frac{{{{x}^{3}}}}{3}-\displaystyle \frac{{3{{x}^{2}}}}{2})} \right|_{0}^{3}+\left. {(\displaystyle \frac{{{{x}^{3}}}}{3}-\displaystyle \frac{{3{{x}^{2}}}}{2})} \right|_{3}^{5}\\&=-\left[ {-4\tfrac{1}{2}} \right]+\left[ {8\tfrac{2}{3}} \right]\\&=13\tfrac{1}{6}\end{align*}[/latex]

Exercise 3.1

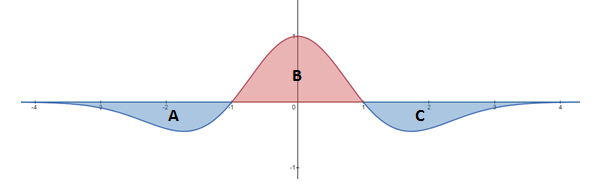
1. State what the sign of each of the areas shown on the graph will be:
   
2. Find the area bounded by the curve [latex]\scriptsize \displaystyle y={{x}^{2}}+x+4[/latex], the x-axis and the ordinates [latex]\scriptsize \displaystyle x=1[/latex] and [latex]\scriptsize \displaystyle x=3[/latex].
3. Find the area contained by the curve [latex]\scriptsize \displaystyle y=x\left( {x\text{ }-\text{ }1} \right)\left( {x\text{ }+\text{ }1} \right)[/latex] and the x-axis.
4. Calculate the value of [latex]\scriptsize \int_{{-1}}^{1}{{x\left( {x\text{ }-\text{ }1} \right)\left( {x\text{ }+\text{ }1} \right)}}dx[/latex]. Compare your answer with that obtained in question three and explain what has happened.

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to find the area of a curve above the x-axis over a given interval.
• How to find the area of a curve below the x-axis over a given interval.
• How to find the total area when a curve crosses the x-axis.
• To use a sketch to arrive at the correct calculation of the area under a curve.

Unit 3: Assessment

Suggested time to complete: 15 minutes

1. Given [latex]\scriptsize f(x)={{x}^{2}}-1[/latex]:
   1. Sketch the curve [latex]\scriptsize f(x)[/latex] and clearly shade the region bounded by [latex]\scriptsize f[/latex] and the lines, [latex]\scriptsize x=1[/latex] and [latex]\scriptsize x=2[/latex].
   2. Calculate the size of the area of the shaded region using integration.
2. Given below is the graph of [latex]\scriptsize y=\cos 2x[/latex] over the interval [latex]\scriptsize \left[ {0,\displaystyle \frac{\pi }{2}} \right][/latex]. Calculate the area bounded by the curve and the x-axis from [latex]\scriptsize x=\displaystyle \frac{\pi }{6}[/latex] to [latex]\scriptsize x=\displaystyle \frac{\pi }{2}[/latex].
   
3. Given below is the graph of [latex]\scriptsize y={{x}^{2}}-4[/latex].
   
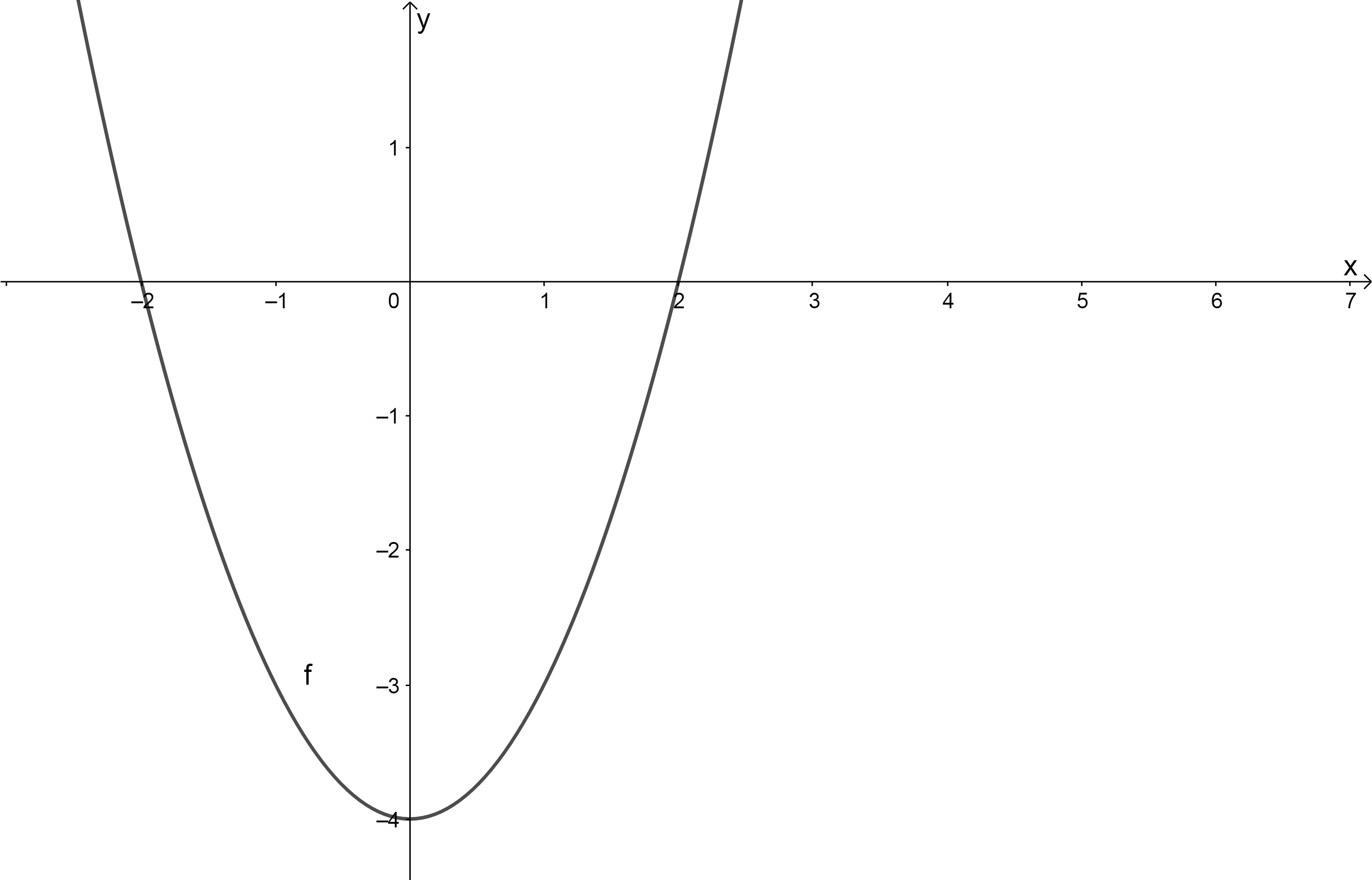
   Determine the area between the graph of [latex]\scriptsize f(x)[/latex], the x-axis and the x-intercepts.

The full solutions are at the end of the unit.

Unit 3: Solutions

Exercise 3.1

1. Area [latex]\scriptsize A[/latex] is completely below the x-axis so the sign of the integral over that interval will be negative.
   Area [latex]\scriptsize B[/latex] is fully above the x-axis so the sign of the integral over that interval will be positive.
   Area [latex]\scriptsize C[/latex] is wholly below the x-axis so the sign of the integral over that interval will be negative.
2. [latex]\scriptsize \displaystyle y={{x}^{2}}+x+4[/latex] has no real roots so the entire curve is above the x-axis. In other words, the graph does not cross the x-axis. Since, the required area is entirely above the x-axis we can simply evaluate the integral between the required limits.
   [latex]\scriptsize \displaystyle \begin{align*}\int_{1}^{3}{{({{x}^{2}}+x+4)dx=\left. {\displaystyle \frac{{{{x}^{3}}}}{3}+\displaystyle \frac{{{{x}^{2}}}}{2}+4x} \right|}}_{1}^{3}\\=\left[ {\displaystyle \frac{{27}}{9}+\displaystyle \frac{9}{2}+12} \right]-\left[ {\displaystyle \frac{1}{3}+\displaystyle \frac{1}{2}+\displaystyle \frac{1}{4}} \right]\\=20\tfrac{2}{3}\end{align*}[/latex]
3. .
   
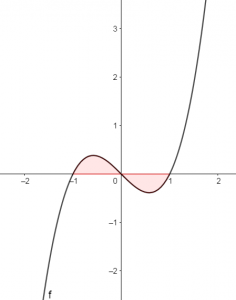
   The graph crosses the x-axis at [latex]\scriptsize x=-1;x=0;x=1[/latex] so the two areas will have different signs.
   Calculate each area separately.
   .
   Area above the x-axis:
   .
   [latex]\scriptsize \begin{align*}\int_{{-1}}^{0}{{({{x}^{3}}-x)}}dx&=\left. {\displaystyle \frac{{{{x}^{4}}}}{4}-\displaystyle \frac{{{{x}^{2}}}}{2}} \right|_{{-1}}^{0}\\&=\left[ {\displaystyle \frac{0}{4}-\displaystyle \frac{0}{2}} \right]-\left[ {\displaystyle \frac{{{{{(-1)}}^{4}}}}{4}-\displaystyle \frac{{{{{(-1)}}^{2}}}}{2}} \right]\\&=\displaystyle \frac{1}{4}\end{align*}[/latex]
   .
   Area below the x-axis:
   .
   [latex]\scriptsize \displaystyle \begin{align*}\int_{0}^{1}{{({{x}^{3}}-x)}}dx&=\left. {\displaystyle \frac{{{{x}^{4}}}}{4}-\displaystyle \frac{{{{x}^{2}}}}{2}} \right|_{0}^{1}\\&=\left[ {\displaystyle \frac{{{{{(1)}}^{4}}}}{4}-\displaystyle \frac{{{{{(1)}}^{2}}}}{2}} \right]-\left[ {\displaystyle \frac{0}{4}-\displaystyle \frac{0}{2}} \right]\\&=-\displaystyle \frac{1}{4}\end{align*}[/latex]
   .
   The total area: [latex]\scriptsize \displaystyle \frac{1}{4}+\displaystyle \frac{1}{4}=\displaystyle \frac{1}{2}[/latex].
   .
   OR
   .
   [latex]\scriptsize \begin{align*}\int_{{-1}}^{0}{{({{x}^{3}}-x)}}dx-\int_{0}^{1}{{({{x}^{3}}-x)}}dx&=\int_{{-1}}^{0}{{({{x}^{3}}-x)}}dx-\int_{0}^{1}{{({{x}^{3}}-x)}}dx\\&=\left. {\displaystyle \frac{{{{x}^{4}}}}{4}-\displaystyle \frac{{{{x}^{2}}}}{2}} \right|_{{-1}}^{0}-\left. {\displaystyle \frac{{{{x}^{4}}}}{4}-\displaystyle \frac{{{{x}^{2}}}}{2}} \right|_{0}^{1}\\&=\left[ {\displaystyle \frac{1}{4}} \right]-\left[ {\displaystyle \frac{{-1}}{4}} \right]\\&=\displaystyle \frac{1}{2}\end{align*}[/latex]
4. .
   [latex]\scriptsize \displaystyle \begin{align*}\int_{{-1}}^{1}{{({{x}^{3}}-x)}}dx&=\left. {\displaystyle \frac{{{{x}^{4}}}}{4}-\displaystyle \frac{{{{x}^{2}}}}{2}} \right|_{{-1}}^{1}\\&=\left[ {\displaystyle \frac{{{{{(1)}}^{4}}}}{4}-\displaystyle \frac{{{{{(1)}}^{2}}}}{2}} \right]-\left[ {\displaystyle \frac{{{{{(-1)}}^{4}}}}{4}-\displaystyle \frac{{{{{(-1)}}^{2}}}}{2}} \right]\\&=-\displaystyle \frac{1}{4}-(-\displaystyle \frac{1}{4})\\&=0\end{align*}[/latex]
   .
   The areas between [latex]\scriptsize \displaystyle x=-1[/latex] and [latex]\scriptsize \displaystyle x=0[/latex], and between [latex]\scriptsize \displaystyle x=0[/latex] and [latex]\scriptsize \displaystyle x=1[/latex], are equal in size. However, one area is above the axis and one is below the axis, so that the integrals have opposite signs and cancel out. Therefore, this does not give the actual area of this curve between those points.

Back to Exercise 3.1

Unit 3: Assessment

1. .
   1. .
      
   2. .
      [latex]\scriptsize \begin{align*}\int_{1}^{2}{{({{x}^{2}}-1}})dx&=\left. {\displaystyle \frac{{{{x}^{3}}}}{3}-x} \right|_{1}^{2}\\&=\left[ {\displaystyle \frac{{{{2}^{3}}}}{3}-2} \right]-\left[ {\displaystyle \frac{{{{1}^{3}}}}{3}-1} \right]\\&=\displaystyle \frac{4}{3}\end{align*}[/latex]
2. First, find the x-intercept. When [latex]\scriptsize y=0[/latex], then [latex]\scriptsize x=\displaystyle \frac{\pi }{4}[/latex].
   
   Next, find the integral from [latex]\scriptsize x=\displaystyle \frac{\pi }{6}[/latex] to [latex]\scriptsize x=\displaystyle \frac{\pi }{4}[/latex] and add that to the integral from [latex]\scriptsize \displaystyle x=\displaystyle \frac{\pi }{4}[/latex] to [latex]\scriptsize x=\displaystyle \frac{\pi }{2}[/latex].
   [latex]\scriptsize \displaystyle \begin{align*}\int_{{\tfrac{\pi }{6}}}^{{\tfrac{\pi }{4}}}{{\cos 2x}}dx&=\left. {\displaystyle \frac{{\sin 2x}}{2}} \right|_{{\tfrac{\pi }{6}}}^{{\tfrac{\pi }{4}}}\\&=\displaystyle \frac{{\sin 2(\displaystyle \frac{\pi }{4})}}{2}-\displaystyle \frac{{\sin 2(\displaystyle \frac{\pi }{6})}}{2}\\&=\displaystyle \frac{{\sin (\displaystyle \frac{\pi }{2})}}{2}-\displaystyle \frac{{\sin (\displaystyle \frac{\pi }{3})}}{2}\\&=\displaystyle \frac{1}{2}-\displaystyle \frac{{\sqrt{3}}}{4}\\&=\displaystyle \frac{{2-\sqrt{3}}}{4}\end{align*}[/latex]
   .
   AND
   .
   [latex]\scriptsize \displaystyle \begin{align*}\int_{{\tfrac{\pi }{4}}}^{{\tfrac{\pi }{2}}}{{\cos 2x}}dx&=\left. {\displaystyle \frac{{\sin 2x}}{2}} \right|_{{\tfrac{\pi }{4}}}^{{\tfrac{\pi }{2}}}\\&=\displaystyle \frac{{\sin 2(\displaystyle \frac{\pi }{2})}}{2}-\displaystyle \frac{{\sin 2(\displaystyle \frac{\pi }{4})}}{2}\\&=\displaystyle \frac{{\sin \pi }}{2}-\displaystyle \frac{{\sin (\displaystyle \frac{\pi }{2})}}{2}\\&=0-\displaystyle \frac{1}{2}\\&=-\displaystyle \frac{1}{2}\end{align*}[/latex]
   Total area: [latex]\scriptsize \displaystyle \displaystyle \frac{{2-\sqrt{3}}}{4}+\displaystyle \frac{1}{2}=0.57[/latex].
3. Since the area we are interested in is completely below the x-axis, you can find the integral from [latex]\scriptsize x=-2[/latex] all the way to [latex]\scriptsize x=2[/latex].
   [latex]\scriptsize \displaystyle \begin{align*}\int_{{-2}}^{2}{{({{x}^{2}}-4)}}dx&=\left. {\displaystyle \frac{{{{x}^{3}}}}{3}-4x} \right|_{{-2}}^{2}\\&=\left[ {\displaystyle \frac{{{{{(2)}}^{3}}}}{3}-4(2)} \right]-\left[ {\displaystyle \frac{{{{{(-2)}}^{3}}}}{3}-4(-2)} \right]\\&=-\displaystyle \frac{{16}}{3}-\displaystyle \frac{{16}}{3}\\&=-\displaystyle \frac{{32}}{3}\end{align*}[/latex]
   [latex]\scriptsize \therefore[/latex] area is [latex]\scriptsize \displaystyle \displaystyle \frac{{32}}{3}[/latex].

Back to Unit 3: Assessment