Complex Numbers: Working with complex numbers
Unit 2: Revise the polar form of complex numbers
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Plot a complex number on the complex plan.
- Find the absolute value of a complex number.
- Convert a complex number from standard (or rectangular) form to polar form.
- Convert a complex number from polar form to standard (or rectangular) form.
- Understand what is meant by the abbreviation when dealing with complex numbers in polar
What you should know
Before you start this unit, make sure you can:
- Represent complex numbers using an Argand diagram. Refer to level 3 subject outcome 1.1 unit 2 if you need help with this.
- Find the modulus argument of a complex number. Refer to level 3 subject outcome 1.1 unit 2 if you need help with this.
- Express complex numbers in polar form. Refer to level 3 subject outcome 1.1 unit 3 if you need help with this.
- Simplify complex numbers in polar form. Refer to level 3 subject outcome 1.1 unit 3 if you need help with this.
- Convert complex numbers from standard/rectangular form to polar form. Refer to level 3 subject outcome 1.1 unit 3 if you need help with this.
- Convert complex numbers from polar form to standard/rectangular form. Refer to level 3 subject outcome 1.1 unit 3 if you need help with this.
Introduction
This unit revises the polar form of complex numbers covered in level 3 subject outcome 1.1 units 2 and 3. It is important that you complete these subject outcomes before continuing.
To understand what the polar form of a complex number is and where it comes from, we need to understand how to plot complex numbers on the complex plane.
The complex plane
We know that we can plot the position of any real number on a number line as shown in Figure 1.

But complex numbers have a real and an imaginary part, therefore we need two numbers to plot them – one for the real part (the x-axis) and one for the imaginary part (the y-axis) placed at right angles to each other to create the complex plane. This is a coordinate system like the Cartesian plane and complex numbers are points on the plane, expressed as ordered pairs.
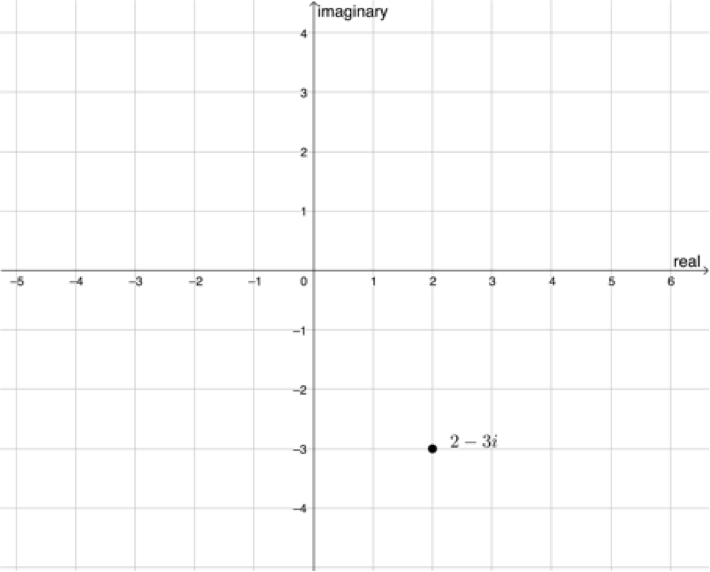
Take the complex number [latex]\scriptsize 2-3i[/latex], for example. We can plot it on the complex plane as shown in Figure 2. It is the point [latex]\scriptsize (2,-3)[/latex].
Exercise 2.1
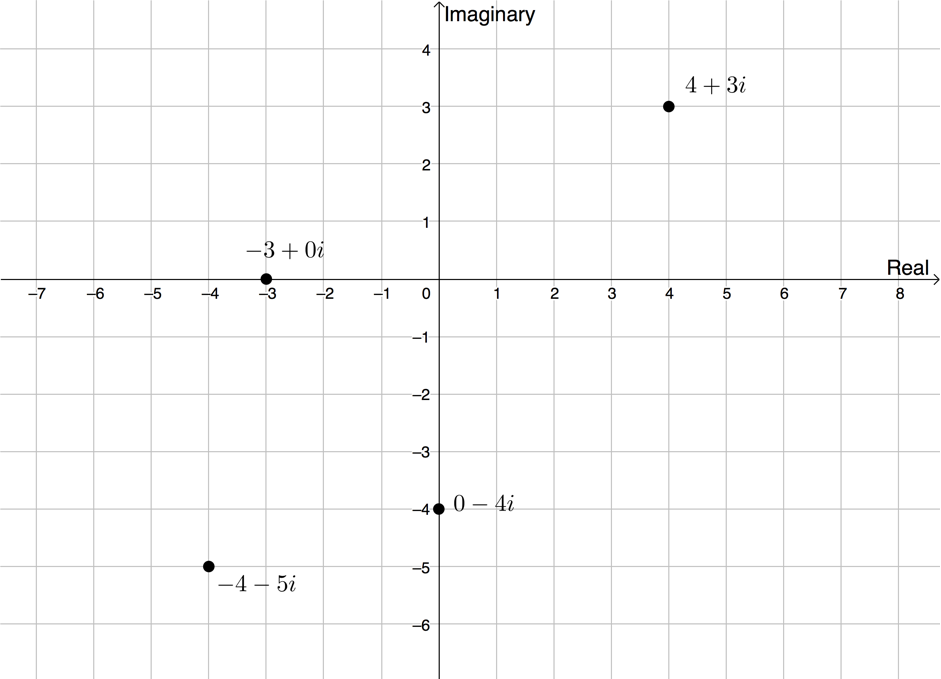
Plot the following complex numbers on the same complex plane:
- [latex]\scriptsize -4-5i[/latex]
- [latex]\scriptsize 4+3i[/latex]
- [latex]\scriptsize -3[/latex]
- [latex]\scriptsize -4i[/latex]
The full solutions are at the end of the unit.
Take note!
An Argand diagram is a plot of complex numbers as points on the complex plane using the x-axis as the real axis and y-axis as the imaginary axis.
The modulus and argument
We often refer to complex numbers as [latex]\scriptsize z[/latex] and the complex plane as the z-plane. We can say that [latex]\scriptsize z=3+4i[/latex].
Figure 3 shows the complex number [latex]\scriptsize z=3+4i[/latex]. The distance of this point from the origin is called the modulus and is designated as [latex]\scriptsize \left| z \right|[/latex].
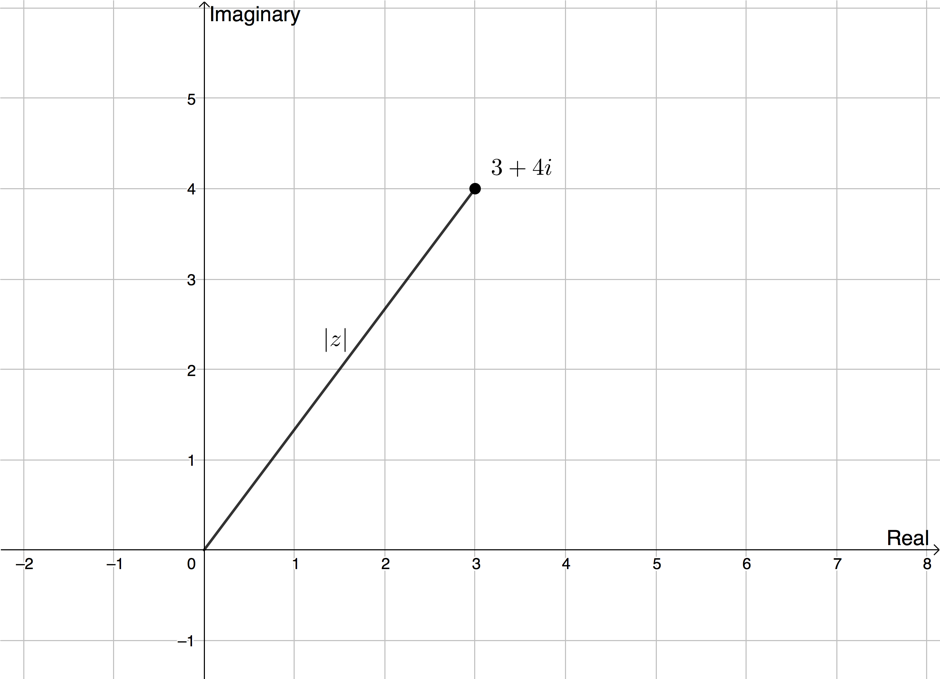
We can determine the modulus by dropping a perpendicular from this point (see Figure 4) and using Pythagoras’ theorem.
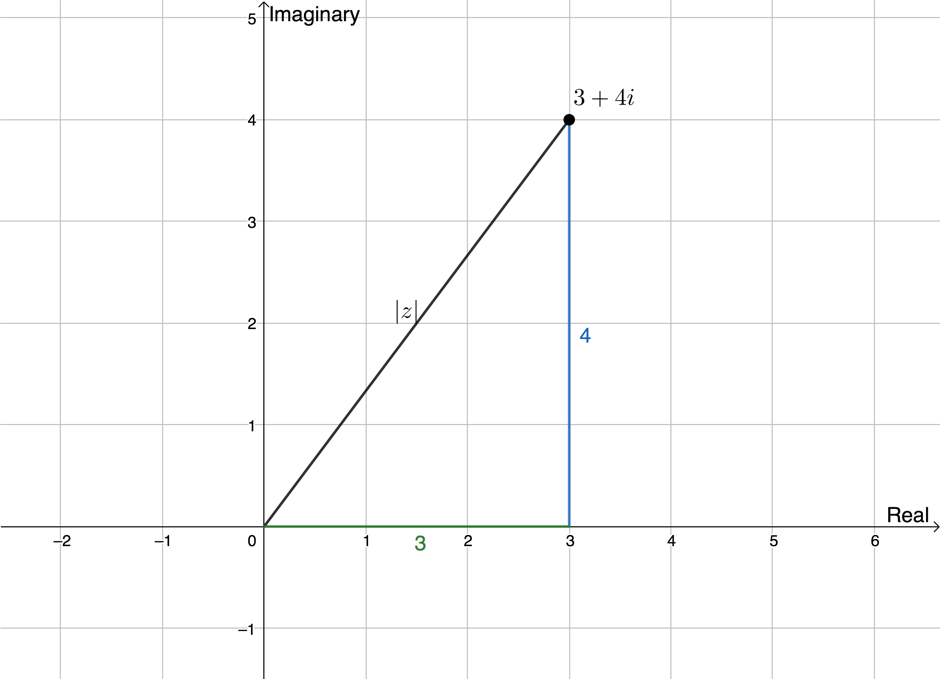
[latex]\scriptsize \begin{align*}{{z}^{2}} & ={{3}^{3}}+{{4}^{2}}\\ & =9+16=25\\\therefore \left| z \right| & =\sqrt{{25}}=5\end{align*}[/latex]
The modulus is always represented as an absolute value with [latex]\scriptsize \left| {} \right|[/latex] signs because it is a length and so always taken as the postive value. In the calculation of [latex]\scriptsize \left| z \right|[/latex] above, we ignore [latex]\scriptsize -5[/latex] as a possible solution.
Example 2.1
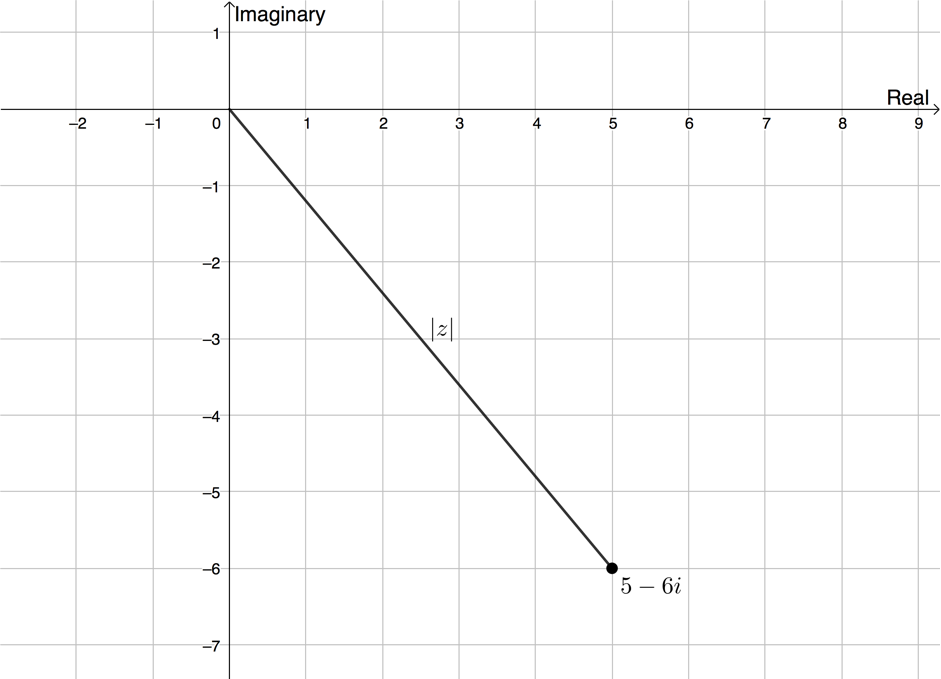
Given [latex]\scriptsize z=5-6i[/latex], find [latex]\scriptsize \left| z \right|[/latex].
Solution
We can plot the complex number [latex]\scriptsize z=5-6i[/latex] on the complex plane.
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{x}^{2}}+{{y}^{2}}}}\quad x\text{ is the real part and }y\text{ is the imaginary part}\\&=\sqrt{{{{5}^{2}}+{{{(-6)}}^{2}}}}\\&=\sqrt{{25+36}}\\&=\sqrt{{61}}\end{align*}[/latex]
Exercise 2.2
Find [latex]\scriptsize \left| z \right|[/latex] in each case:
- [latex]\scriptsize z=1+7i[/latex]
- [latex]\scriptsize z=-3-5i[/latex]
- [latex]\scriptsize z=-4+\displaystyle \frac{3}{2}i[/latex]
- [latex]\scriptsize z=-\sqrt{5}-\sqrt{{-6}}[/latex]
The full solutions are at the end of the unit.
The modulus is not enough to fully define the position of a complex number on the complex plane. Figure 5 shows two complex numbers, [latex]\scriptsize {{z}_{1}}=4+3i[/latex] and [latex]\scriptsize {{z}_{2}}=3-4i[/latex]. For each, [latex]\scriptsize \left| z \right|=5[/latex].
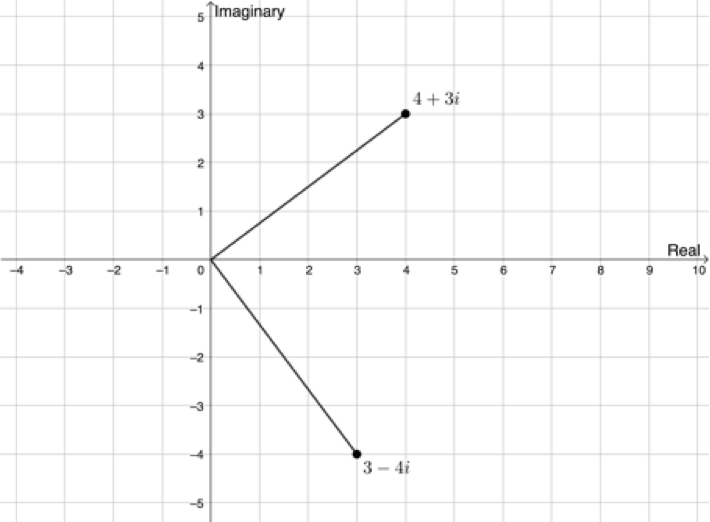
We also need to know the argument, the angle the line representing the modulus makes with the positive x-axis (see Figure 6).
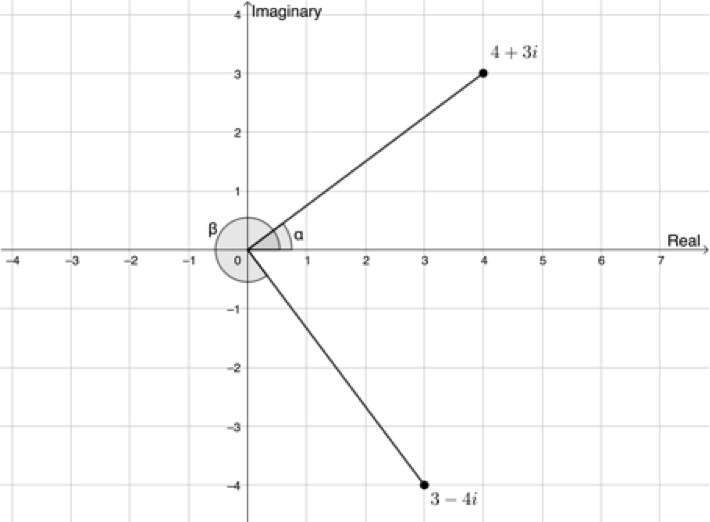
In Figure 6 we see that [latex]\scriptsize \sin \alpha =\displaystyle \frac{y}{r}=\displaystyle \frac{3}{5}[/latex] or that [latex]\scriptsize \cos \alpha =\displaystyle \frac{x}{r}=\displaystyle \frac{4}{5}[/latex]. Therefore, [latex]\scriptsize \alpha ={{36.870}^\circ}[/latex]. This answer makes sense because [latex]\scriptsize {{z}_{1}}=4+3i[/latex] is in the first quadrant.
Also, we can say that [latex]\scriptsize \sin \beta =\displaystyle \frac{y}{r}=\displaystyle \frac{{-4}}{5}[/latex] or that [latex]\scriptsize \cos \beta =\displaystyle \frac{x}{r}=\displaystyle \frac{3}{5}[/latex]. Therefore, [latex]\scriptsize \beta =-{{53.130}^\circ}[/latex]. This makes sense because [latex]\scriptsize {{z}_{2}}=3-4i[/latex] is in the fourth quadrant.
With the modulus and the argument, we can uniquely specify the position of any complex number on the complex plane.
Take note!
The value of the modulus [latex]\scriptsize \left| z \right|[/latex] is the same as the value of [latex]\scriptsize r[/latex] in [latex]\scriptsize \sin \theta =\displaystyle \frac{y}{r}[/latex] or [latex]\scriptsize \cos \theta =\displaystyle \frac{x}{r}[/latex].
Take note!
When calculating the argument, it is important that you draw a sketch of the position of [latex]\scriptsize z[/latex] on the complex plane to determine which quadrant the point is in. The three trigonometric ratios still follow the CAST diagram on the complex plane (see Figure 7).

Example 2.2
Determine the modulus and the argument of [latex]\scriptsize z=-2-\sqrt{{-3}}[/latex].
Solution
First, write the complex number in standard form [latex]\scriptsize a+bi[/latex].
[latex]\scriptsize z=-2-\sqrt{{-3}}=-2-\sqrt{3}i[/latex]
[latex]\scriptsize z[/latex] lies in the third quadrant because [latex]\scriptsize x[/latex] ([latex]\scriptsize -2[/latex]) and [latex]\scriptsize y[/latex] ([latex]\scriptsize -\sqrt{3}[/latex]) are both negative.
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\&=\sqrt{{{{{(-2)}}^{2}}+{{{\left( {-\sqrt{3}} \right)}}^{2}}}}\\&=\sqrt{{4+3}}\\&=\sqrt{7}\end{align*}[/latex]
To find the argument, start by finding a reference angle ([latex]\scriptsize \alpha[/latex]) using a positive ratio of sine or cosine.
[latex]\scriptsize \begin{align*}\sin \alpha & =\displaystyle \frac{y}{r}=\displaystyle \frac{{\sqrt{3}}}{{\sqrt{7}}}\\\therefore \alpha & ={{40.89}^\circ}\end{align*}[/latex]
But [latex]\scriptsize z[/latex] lies in the third quadrant. Therefore, [latex]\scriptsize \theta ={{180}^\circ}+{{40.89}^\circ}={{220.89}^\circ}[/latex].
Take note!
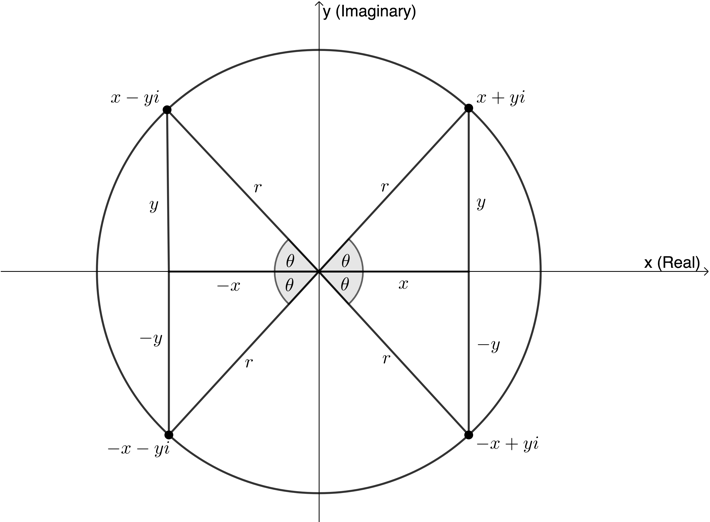
When finding the argument, remember that you need to pay attention to which quadrant the complex number is in. A useful strategy can be to make the ratio for [latex]\scriptsize \sin \theta =\displaystyle \frac{y}{r}[/latex] or [latex]\scriptsize \cos \theta =\displaystyle \frac{x}{r}[/latex] positive initially, in order to find the acute reference angle [latex]\scriptsize \theta[/latex], and then to transfer this angle into the necessary quadrant as indicated in Figure 8. To transfer these angles, use the following identities:
- Second quadrant: [latex]\scriptsize {{180}^\circ}-\theta[/latex]
- Third quadrant: [latex]\scriptsize {{180}^\circ}+\theta[/latex]
- Fourth quadrant: [latex]\scriptsize {{360}^\circ}-\theta[/latex]
Exercise 2.3
Determine the modulus and the argument of the following complex numbers, leaving your moduli in surd form:
- [latex]\scriptsize z=-1-8i[/latex]
- [latex]\scriptsize z=-2+2i[/latex]
- [latex]\scriptsize z=4-3i[/latex]
The full solutions are at the end of the unit.
Polar form
We say that [latex]\scriptsize z=2-3i[/latex] is written in standard or rectangular form where the number is expressed in terms of a real and imaginary component. The polar form of a complex number expresses the number in terms of its modulus and argument.
Suppose we have a complex number [latex]\scriptsize z=x+yi[/latex]. We can represent this with an Argand diagram (see Figure 9).
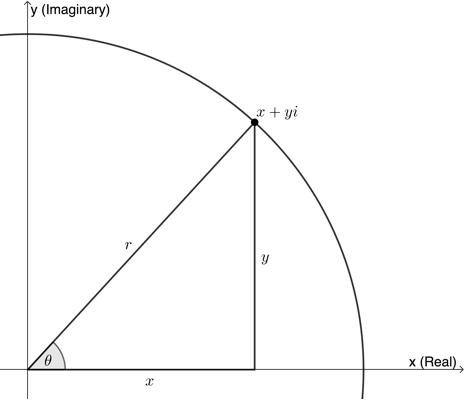
Now we know that [latex]\scriptsize \cos \theta =\displaystyle \frac{x}{r}[/latex] and [latex]\scriptsize \sin \theta =\displaystyle \frac{y}{r}[/latex]. Therefore, [latex]\scriptsize x=r\cos \theta[/latex] and [latex]\scriptsize y=r\sin \theta[/latex].
So, the point [latex]\scriptsize (x,y)[/latex] has coordinates given by [latex]\scriptsize x=r\cos \theta[/latex] and [latex]\scriptsize y=r\sin \theta[/latex] where [latex]\scriptsize r=\sqrt{{{{x}^{2}}+{{y}^{2}}}}[/latex]. Therefore:
[latex]\scriptsize \begin{align*}z&=x+yi\\&=r\cos \theta +(r\sin \theta )i\\&=r(\cos \theta +i\sin \theta )\end{align*}[/latex]
Take note!
The polar form of a complex number:
[latex]\scriptsize \begin{align*}z&=x+yi\\&=r\cos \theta +(r\sin \theta )i\\&=r(\cos \theta +i\sin \theta )\\&=r\text{cis}\theta \end{align*}[/latex]
where [latex]\scriptsize r=\left| z \right|[/latex] and [latex]\scriptsize \theta[/latex] is the argument.
Example 2.3
Find the polar form of [latex]\scriptsize z=-4-4i[/latex].
Solution
Step 1: Determine [latex]\scriptsize r[/latex] (or [latex]\scriptsize \left| z \right|[/latex])
[latex]\scriptsize \begin{align*}r&=\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\&=\sqrt{{{{{(-4)}}^{2}}+{{{(-4)}}^{2}}}}\\&=\sqrt{{16+16}}\\&=\sqrt{{32}}\\&=4\sqrt{2}\end{align*}[/latex]
Step 2: Determine [latex]\scriptsize \theta[/latex]
[latex]\scriptsize z[/latex] is in the third quadrant. Find reference angle [latex]\scriptsize \alpha[/latex].
[latex]\scriptsize \begin{align*}\cos \alpha & =\displaystyle \frac{x}{r}=\displaystyle \frac{4}{{4\sqrt{2}}}=\displaystyle \frac{1}{{\sqrt{2}}}\\\therefore \alpha & ={{45}^\circ}\end{align*}[/latex]
Therefore [latex]\scriptsize \theta ={{180}^\circ}+{{45}^\circ}={{225}^\circ}[/latex].
Step 3: Write the solution
[latex]\scriptsize \begin{align*}z&=r(\cos \theta +i\sin \theta )\\&=4\sqrt{2}(\cos {{225}^\circ}+i\sin {{225}^\circ})\\&=4\sqrt{2}\text{cis22}{{5}^\circ}\end{align*}[/latex]
Exercise 2.4
Write the following complex numbers in polar form:
- [latex]\scriptsize z=5+12i[/latex]
- [latex]\scriptsize z=-7-3i[/latex]
- [latex]\scriptsize z=\sqrt{5}-\sqrt{{-6}}[/latex]
The full solutions are at the end of the unit.
Convert polar form to rectangular form
Sometimes it is necessary to convert a complex number in polar form into standard or rectangular form. To do this, we need to first evaluate the trigonometric functions [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \sin \theta[/latex], then multiply through by [latex]\scriptsize r[/latex].
Example 2.4
Convert [latex]\scriptsize z=12\text{cis4}{{\text{5}}^\circ}[/latex] into standard/rectangular form.
Solution
Step 1: Evaluate [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \sin \theta[/latex]
We can use the fact that [latex]\scriptsize {{45}^\circ}[/latex] is a special angle to evaluate without a calculator.
[latex]\scriptsize \cos {{45}^\circ}=\displaystyle \frac{1}{{\sqrt{2}}}[/latex]
[latex]\scriptsize \sin {{45}^\circ}=\displaystyle \frac{1}{{\sqrt{2}}}[/latex]
Step 2: Find the standard form
[latex]\scriptsize z[/latex] is in the first quadrant where cosine and sine are positive.
[latex]\scriptsize \begin{align*}z&=12(\cos {{45}^\circ}+i\sin {{45}^\circ})\\&=12\left( {\displaystyle \frac{1}{{\sqrt{2}}}+\displaystyle \frac{1}{{\sqrt{2}}}i} \right)\\&=\displaystyle \frac{{12}}{{\sqrt{2}}}+\displaystyle \frac{{12}}{{\sqrt{2}}}i\\&=\displaystyle \frac{{12\sqrt{2}}}{2}+\displaystyle \frac{{12\sqrt{2}}}{2}i\\&=6\sqrt{2}+6\sqrt{2}i\end{align*}[/latex]
The complex number in standard form is [latex]\scriptsize z=6\sqrt{2}+6\sqrt{2}i[/latex].
Example 2.5
Convert [latex]\scriptsize z=4\text{cis15}{{\text{0}}^\circ}[/latex] into standard/rectangular form.
Solution
Step 1: Evaluate [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \sin \theta[/latex]
[latex]\scriptsize {{120}^\circ}[/latex] is not a special angle but [latex]\scriptsize {{180}^\circ}-{{150}^\circ}={{30}^\circ}[/latex] is a special angle. Therefore, we can evaluate [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \sin \theta[/latex] without a calculator and transfer the angle into the correct quadrant, in this case, the second quadrant.
[latex]\scriptsize \cos {{30}^\circ}=\displaystyle \frac{{\sqrt{3}}}{2}[/latex]
[latex]\scriptsize \sin {{30}^\circ}=\displaystyle \frac{1}{2}[/latex]
Step 2: Find the standard form
We know that the complex number is in the second quadrant where cosine is negative and sine is positive.
[latex]\scriptsize \begin{align*}z&=4(\cos {{150}^\circ}+i\sin {{150}^\circ})\\&=4\left( {-\displaystyle \frac{{\sqrt{3}}}{2}+\displaystyle \frac{1}{2}i} \right)\quad \text{Remember that cosine is negative in the second quadrant}\\&=-2\sqrt{3}+2i\end{align*}[/latex]
The complex number in standard form is [latex]\scriptsize z=-2\sqrt{3}+2i[/latex].
Example 2.6
Convert [latex]\scriptsize z=3\text{cis24}{{\text{3}}^\circ}[/latex] into standard/rectangular form.
Solution
Step 1: Evaluate [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \sin \theta[/latex]
[latex]\scriptsize {{243}^\circ}[/latex] is not a special angle and cannot be reduced to a special angle. Therefore, we have to evaluate [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \sin \theta[/latex] with a calculator. The complex number is in the third quadrant.
[latex]\scriptsize \cos {{243}^\circ}=-0.454[/latex]
[latex]\scriptsize \sin {{243}^\circ}=-0.891[/latex]
Step 2: Find the standard form
We know that the complex number is in the third quadrant where cosine and sine are negative.
[latex]\scriptsize \begin{align*}z&=3(\cos {{243}^\circ}+i\sin {{243}^\circ})\\&=3\left( {-0.454-0.891i} \right)\\&=-1.362-2.673i\end{align*}[/latex]
The complex number in standard form is [latex]\scriptsize z=-1.362-2.673i[/latex].
Exercise 2.5
Convert the following complex numbers into standard/rectangular form:
- [latex]\scriptsize z=\sqrt{3}\text{cis}{{45}^\circ}[/latex]
- [latex]\scriptsize z=\sqrt{7}\text{cis21}{{\text{0}}^\circ}[/latex]
- [latex]\scriptsize z=3\text{cis3}{{40}^\circ}[/latex]
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- How to plot a complex number on the complex plane.
- How to find the absolute value or modulus of a complex number.
- How to convert a complex number from standard (or rectangular) form to polar form.
- How to convert a complex number from polar form to standard (or rectangular) form.
- How to use the [latex]\scriptsize \text{cis}[/latex] shorthand for the polar form.
Unit 2: Assessment
Suggested time to complete: 25 minutes
- Given [latex]\scriptsize z=-1+\sqrt{3}i[/latex]:
- Write down the conjugate of [latex]\scriptsize z[/latex].
- Calculate the modulus of [latex]\scriptsize z[/latex].
- Determine the argument of [latex]\scriptsize z[/latex].
- Write [latex]\scriptsize z[/latex] in polar form.
- Write the following complex numbers in polar form:
- [latex]\scriptsize z=\displaystyle \frac{3}{2}-7i[/latex]
- [latex]\scriptsize z=-4+\sqrt{{-8}}[/latex]
- [latex]\scriptsize z=\sqrt{{13}}-\sqrt{{-13}}[/latex]
- [latex]\scriptsize z=-6+3.543i[/latex]
- Write the following complex numbers in standard form:
- [latex]\scriptsize z=13\text{cis}{{330}^\circ}[/latex]
- [latex]\scriptsize z=\sqrt{7}\text{cis22}{{\text{5}}^\circ}[/latex]
- [latex]\scriptsize z=\displaystyle \frac{2}{{\sqrt{3}}}\text{cis12}{{\text{0}}^\circ}[/latex]
- [latex]\scriptsize z=4\text{cis16}{{\text{0}}^\circ}[/latex]
The full solutions are at the end of the unit.
Unit 2: Solutions
Exercise 2.1
Exercise 2.2
- .
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{1}^{2}}+{{7}^{2}}}}\\&=\sqrt{{1+49}}\\&=\sqrt{{50}}\\&=5\sqrt{2}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{{(-3)}}^{2}}+{{{(-5)}}^{2}}}}\text{ }\\&=\sqrt{{9+25}}\\&=\sqrt{{34}}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\mid z\mid&=\sqrt{(-4)^2+\left(\displaystyle \frac{3}{2}\right)^2}\\ &=\sqrt{16+\displaystyle \frac{9}{4}}\\ &=\sqrt{\displaystyle \frac{64+9}{4}}\\ &=\sqrt{\displaystyle \frac{73}{4}}\\ &=\displaystyle \frac{\sqrt{73}}{2}\end{align*}[/latex] - .
[latex]\scriptsize z=-\sqrt{5}-\sqrt{{-6}}=-\sqrt{5}-\sqrt{6}i[/latex]
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{{\left( {-\sqrt{5}} \right)}}^{2}}+{{{\left( {-\sqrt{6}} \right)}}^{2}}}}\\&=\sqrt{{5+6}}\\&=\sqrt{{11}}\end{align*}[/latex]
Exercise 2.3
- [latex]\scriptsize z=-1-8i[/latex]
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{{(-1)}}^{2}}+{{{(-8)}}^{2}}}}\\&=\sqrt{{1+64}}\\&=\sqrt{{65}}\end{align*}[/latex]
[latex]\scriptsize z[/latex] is in the third quadrant. Find reference angle [latex]\scriptsize \alpha[/latex].
[latex]\scriptsize \begin{align*}\sin \alpha & =\displaystyle \frac{8}{{\sqrt{{65}}}}\\\therefore \alpha & ={{82.87}^\circ}\end{align*}[/latex]
Therefore, [latex]\scriptsize \theta ={{180}^\circ}+\alpha ={{262.87}^\circ}[/latex]. - [latex]\scriptsize z=-2+2i[/latex]
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{{(-2)}}^{2}}+{{2}^{2}}}}\\&=\sqrt{{4+4}}\\&=\sqrt{8}\\&=2\sqrt{2}\end{align*}[/latex]
[latex]\scriptsize z[/latex] is in the second quadrant. Find reference angle [latex]\scriptsize \alpha[/latex].
[latex]\scriptsize \begin{align*}\sin \alpha & =\displaystyle \frac{2}{{2\sqrt{2}}}=\displaystyle \frac{1}{{\sqrt{2}}}\\\therefore \alpha & ={{45}^\circ}\end{align*}[/latex]
Therefore, [latex]\scriptsize \theta ={{180}^\circ}-\alpha ={{135}^\circ}[/latex]. - [latex]\scriptsize z=4-3i[/latex]
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{{(4)}}^{2}}+{{{(-3)}}^{2}}}}\\&=\sqrt{{16+9}}\\&=\sqrt{{25}}\\&=5\end{align*}[/latex]
[latex]\scriptsize z[/latex] is in the fourth quadrant. Find reference angle [latex]\scriptsize \alpha[/latex].
[latex]\scriptsize \begin{align*}\sin \alpha & =\displaystyle \frac{3}{5}\\\therefore \alpha & ={{36.87}^\circ}\end{align*}[/latex]
Therefore, [latex]\scriptsize \theta ={{360}^\circ}-\alpha ={{323.13}^\circ}[/latex].
Exercise 2.4
- [latex]\scriptsize z=5+12i[/latex]
[latex]\scriptsize \begin{align*}r&=\sqrt{{{{{(5)}}^{2}}+{{{(12)}}^{2}}}}\\&=\sqrt{{25+144}}\\&=\sqrt{{169}}\\&=13\end{align*}[/latex]
[latex]\scriptsize z[/latex] is in the first quadrant.
[latex]\scriptsize \begin{align*}\sin \theta & =\displaystyle \frac{{12}}{{13}}\\\therefore \theta & ={{67.38}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}z&=r(\cos \theta +i\sin \theta )\\&=13(\cos {{67.38}^\circ}+i\sin {{67.38}^\circ})\\&=13\text{cis}{{67.38}^\circ}\end{align*}[/latex] - [latex]\scriptsize z=-7-3i[/latex]
[latex]\scriptsize \begin{align*}r&=\sqrt{{{{{(-7)}}^{2}}+{{{(-3)}}^{2}}}}\\&=\sqrt{{49+9}}\\&=\sqrt{{58}}\end{align*}[/latex]
[latex]\scriptsize z[/latex] is in the third quadrant.
[latex]\scriptsize \begin{align*}\sin \alpha & =\displaystyle \frac{3}{{\sqrt{{58}}}}\\\therefore \alpha &={{23.20}^\circ}\end{align*}[/latex]
Therefore, [latex]\scriptsize \theta ={{180}^\circ}+{{23.20}^\circ}={{203.20}^\circ}[/latex]
[latex]\scriptsize \begin{align*}z&=r(\cos \theta +i\sin \theta )\\&=\sqrt{{58}}(\cos {{203.30}^\circ}+i\sin {{203.20}^\circ})\\&=\sqrt{{58}}\text{cis}{{203.20}^\circ}\end{align*}[/latex] - [latex]\scriptsize z=\sqrt{5}-\sqrt{{-6}}=\sqrt{5}-\sqrt{6}i[/latex]
[latex]\scriptsize \begin{align*}r&=\sqrt{{{{{\left( {\sqrt{5}} \right)}}^{2}}+{{{\left( {\sqrt{6}} \right)}}^{2}}}}\\&=\sqrt{{5+6}}\\&=\sqrt{{11}}\end{align*}[/latex]
[latex]\scriptsize z[/latex] is in the fourth quadrant.
[latex]\scriptsize \begin{align*}\sin \alpha & =\displaystyle \frac{{\sqrt{6}}}{{\sqrt{{11}}}}\\\therefore \alpha &={{47.61}^\circ}\end{align*}[/latex]
Therefore, [latex]\scriptsize \theta ={{360}^\circ}-{{47.61}^\circ}={{312.39}^\circ}[/latex].
[latex]\scriptsize \begin{align*}z&=r(\cos \theta +i\sin \theta )\\&=\sqrt{{11}}(\cos {{312.39}^\circ}+i\sin {{312.39}^\circ})\\&=\sqrt{{11}}\text{cis}{{312.39}^\circ}\end{align*}[/latex]
Exercise 2.5
- [latex]\scriptsize z=\sqrt{3}\text{cis}{{45}^\circ}[/latex]
[latex]\scriptsize \cos {{45}^\circ}=\displaystyle \frac{1}{{\sqrt{2}}}[/latex]
[latex]\scriptsize \sin {{45}^\circ}=\displaystyle \frac{1}{{\sqrt{2}}}[/latex]
[latex]\scriptsize \begin{align*}z&=\sqrt{3}\left( {\displaystyle \frac{1}{{\sqrt{2}}}+\displaystyle \frac{1}{{\sqrt{2}}}i} \right)\\&=\displaystyle \frac{{\sqrt{3}}}{{\sqrt{2}}}+\displaystyle \frac{{\sqrt{3}}}{{\sqrt{2}}}i\\&=\displaystyle \frac{{\sqrt{2}\sqrt{3}}}{2}+\displaystyle \frac{{\sqrt{2}\sqrt{3}}}{2}i\end{align*}[/latex] - [latex]\scriptsize z=\sqrt{7}\text{cis21}{{\text{0}}^\circ}[/latex]
[latex]\scriptsize \cos {{210}^\circ}=\cos ({{180}^\circ}+{{30}^\circ})=-\cos {{30}^\circ}=-\displaystyle \frac{{\sqrt{3}}}{2}[/latex]
[latex]\scriptsize \sin {{210}^\circ}=\sin ({{180}^\circ}+{{30}^\circ})=-\sin {{30}^\circ}=-\displaystyle \frac{1}{2}[/latex]
[latex]\scriptsize \begin{align*}z&=\sqrt{7}\left( {-\displaystyle \frac{{\sqrt{3}}}{2}-\displaystyle \frac{1}{2}i} \right)\\&=\displaystyle \frac{{\sqrt{{21}}}}{2}-\displaystyle \frac{{\sqrt{7}}}{2}i\end{align*}[/latex] - [latex]\scriptsize z=3\text{cis3}{{40}^\circ}[/latex]
[latex]\scriptsize \cos {{340}^\circ}=0.940[/latex]
[latex]\scriptsize \sin {{340}^\circ}=-0.342[/latex]
[latex]\scriptsize \begin{align*}z&=3\left( {0.940-0.342i} \right)\\&=2.82-1.026i\end{align*}[/latex]
Unit 2: Assessment
- [latex]\scriptsize z=-1+\sqrt{3}i[/latex]
- [latex]\scriptsize -1-\sqrt{3}i[/latex]
- .
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{{\left( {-1} \right)}}^{2}}+{{{\left( {\sqrt{3}} \right)}}^{2}}}}\\&=\sqrt{{1+3}}\\&=\sqrt{4}\\&=2\end{align*}[/latex] - [latex]\scriptsize z[/latex] is in the second quadrant.
[latex]\scriptsize \begin{align*}\sin \alpha &=\displaystyle \frac{{\sqrt{3}}}{2}\\\therefore \alpha &={{60}^\circ}\end{align*}[/latex]
[latex]\scriptsize \theta ={{180}^\circ}-{{60}^\circ}={{120}^\circ}[/latex] - .
EQU
- .
- [latex]\scriptsize z=\displaystyle \frac{3}{2}-7i[/latex]
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{{\left( {\displaystyle \frac{3}{2}} \right)}}^{2}}+{{{\left( {-7} \right)}}^{2}}}}\\&=\sqrt{{\displaystyle \frac{9}{4}+49}}\\&=\sqrt{{\displaystyle \frac{{9+196}}{4}}}\\&=\sqrt{{\displaystyle \frac{{205}}{4}}}\\&=\displaystyle \frac{{\sqrt{{205}}}}{2}\end{align*}[/latex]
[latex]\scriptsize z[/latex] is in the fourth quadrant.
[latex]\scriptsize \begin{align*}\sin \alpha &=\displaystyle \frac{7}{{\displaystyle \frac{{\sqrt{{205}}}}{2}}}\\\therefore \alpha &={{77.91}^\circ}\end{align*}[/latex]
[latex]\scriptsize \theta ={{360}^\circ}-{{77.91}^\circ}={{282.09}^\circ}[/latex]
[latex]\scriptsize \begin{align*}z&=\displaystyle \frac{{\sqrt{{205}}}}{2}(\cos {{282.09}^\circ}+i\sin {{282.09}^\circ})\\&=\displaystyle \frac{{\sqrt{{205}}}}{2}\text{cis}{{282.09}^\circ}\end{align*}[/latex] - [latex]\scriptsize z=-4+\sqrt{{-8}}=-4+\sqrt{8}i[/latex]
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{{(-4)}}^{2}}+{{8}^{2}}}}\\&=\sqrt{{16+64}}\\&=\sqrt{{80}}\\&=4\sqrt{5}\end{align*}[/latex]
[latex]\scriptsize z[/latex] is in the second quadrant.
[latex]\scriptsize \begin{align*}\sin \alpha &=\displaystyle \frac{{\sqrt{8}}}{{4\sqrt{5}}}\\\therefore \alpha &={{18.43}^\circ}\end{align*}[/latex]
[latex]\scriptsize \theta ={{180}^\circ}-{{18.43}^\circ}={{161.57}^\circ}[/latex]
[latex]\scriptsize \begin{align*}z&=4\sqrt{5}(\cos {{161.57}^\circ}+i\sin {{161.57}^\circ})\\&=4\sqrt{5}\text{cis}{{161.57}^\circ}\end{align*}[/latex] - [latex]\scriptsize z=\sqrt{{13}}-\sqrt{{-13}}=\sqrt{{13}}-\sqrt{{13}}i[/latex]
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{{\left( {\sqrt{{13}}} \right)}}^{2}}+{{{\left( {-\sqrt{{13}}} \right)}}^{2}}}}\\&=\sqrt{{13+13}}\\&=\sqrt{{26}}\end{align*}[/latex]
[latex]\scriptsize z[/latex] is in the fourth quadrant.
[latex]\scriptsize \begin{align*}\sin \alpha &=\displaystyle \frac{{\sqrt{{13}}}}{{\sqrt{{26}}}}=\displaystyle \frac{{\sqrt{{13}}}}{{\sqrt{2}\sqrt{{13}}}}=\displaystyle \frac{1}{{\sqrt{2}}}\\\therefore \alpha &={{45}^\circ}\end{align*}[/latex]
[latex]\scriptsize \theta ={{360}^\circ}-{{45}^\circ}={{315}^\circ}[/latex]
[latex]\scriptsize \begin{align*}z&=\sqrt{{26}}(\cos {{315}^\circ}+i\sin {{315}^\circ})\\&=\sqrt{{26}}\text{cis31}{{\text{5}}^\circ}\end{align*}[/latex] - [latex]\scriptsize z=-6+3.543i[/latex]
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{{(-6)}}^{2}}+{{{3.543}}^{2}}}}\\&=\sqrt{{36+12.55}}\\&=\sqrt{{48.55}}\end{align*}[/latex]
[latex]\scriptsize z[/latex] is in the second quadrant.
[latex]\scriptsize \begin{align*}\sin \alpha &=\displaystyle \frac{{3.543}}{{\sqrt{{48.55}}}}\\\therefore \alpha &={{30.56}^\circ}\end{align*}[/latex]
[latex]\scriptsize \theta ={{180}^\circ}-{{30.56}^\circ}={{149.44}^\circ}[/latex]
[latex]\scriptsize \begin{align*}z&=\sqrt{{48.55}}(\cos {{149.44}^\circ}+i\sin {{149.44}^\circ})\\&=\sqrt{{48.55}}\text{cis}{{149.44}^\circ}\end{align*}[/latex]
- [latex]\scriptsize z=\displaystyle \frac{3}{2}-7i[/latex]
- .
- [latex]\scriptsize z=13\text{cis}{{330}^\circ}[/latex]
[latex]\scriptsize \cos {{330}^\circ}=\cos ({{360}^\circ}-{{30}^\circ})=\cos {{30}^\circ}=\displaystyle \frac{{\sqrt{3}}}{2}[/latex]
[latex]\scriptsize \sin {{330}^\circ}=\sin ({{360}^\circ}-{{30}^\circ})=-\sin {{30}^\circ}=-\displaystyle \frac{1}{2}[/latex]
[latex]\scriptsize \begin{align*}z&=13\left( {\displaystyle \frac{{\sqrt{3}}}{2}-\displaystyle \frac{1}{2}i} \right)\\&=\displaystyle \frac{{13\sqrt{3}}}{2}-\displaystyle \frac{{13}}{2}i\end{align*}[/latex] - [latex]\scriptsize z=\sqrt{7}\text{cis22}{{\text{5}}^\circ}[/latex]
[latex]\scriptsize \cos {{225}^\circ}=\cos ({{180}^\circ}+{{45}^\circ})=-\cos {{45}^\circ}=-\displaystyle \frac{1}{{\sqrt{2}}}[/latex]
[latex]\scriptsize \sin {{225}^\circ}=\sin ({{180}^\circ}+{{45}^\circ})=-\sin {{45}^\circ}=-\displaystyle \frac{1}{{\sqrt{2}}}[/latex]
[latex]\scriptsize \begin{align*}z&=\sqrt{7}\left( {-\displaystyle \frac{1}{{\sqrt{2}}}-\displaystyle \frac{1}{{\sqrt{2}}}i} \right)\\&=-\displaystyle \frac{{\sqrt{7}}}{{\sqrt{2}}}-\displaystyle \frac{{\sqrt{7}}}{{\sqrt{2}}}i\end{align*}[/latex] - [latex]\scriptsize z=\displaystyle \frac{2}{{\sqrt{3}}}\text{cis12}{{\text{0}}^\circ}[/latex]
[latex]\scriptsize \cos {{120}^\circ}=\cos ({{180}^\circ}-{{60}^\circ})=-\cos {{60}^\circ}=-\displaystyle \frac{1}{2}[/latex]
[latex]\scriptsize \sin {{120}^\circ}=\sin ({{180}^\circ}-{{60}^\circ})=\sin {{60}^\circ}=\displaystyle \frac{{\sqrt{3}}}{2}[/latex]
[latex]\scriptsize \begin{align*}z&=\displaystyle \frac{2}{{\sqrt{3}}}\left( {-\displaystyle \frac{1}{2}+\displaystyle \frac{{\sqrt{3}}}{2}i} \right)\\&=-\displaystyle \frac{1}{{\sqrt{3}}}+i\end{align*}[/latex] - [latex]\scriptsize z=4\text{cis16}{{\text{0}}^\circ}[/latex]
[latex]\scriptsize \cos {{160}^\circ}=-0.940[/latex]
[latex]\scriptsize \sin {{160}^\circ}=0.342[/latex]
[latex]\scriptsize \begin{align*}z&=4\left( {-0.940+0.342i} \right)\\&=-3.76+1.368i\end{align*}[/latex]
- [latex]\scriptsize z=13\text{cis}{{330}^\circ}[/latex]
Media Attributions
- figure1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example2.1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure6 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure7 © DHET is licensed under a CC BY (Attribution) license
- transformation © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- takenotecis © DHET is licensed under a CC BY (Attribution) license
- exercise2.1A © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license