Space, shape and measurement: Explore, interpret and justify geometric relationships
Unit 1: Finding angles of straight lines and triangles
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Use properties of angles on straight lines and angles in a triangle to find unknown angles including:
- angles of a triangle
- exterior angles
- straight lines
- vertically opposite angles
- corresponding angles
- co-interior angles
- alternate angles
What you should know
Before you start this unit, make sure you can:
- Work with triangles and the measurement of angles. Level 2 subject outcome 3.2 will remind you of these basics.
Introduction
The word ‘geometry’ comes from two Greek words ‘geo’ meaning earth and ‘metria’ meaning measure. It is the area of mathematics that deals with objects and spatial arrangements. Analytical geometry, as we studied in subject outcome 3.1, deals with these objects and their spatial arrangements by using the Cartesian coordinate system and algebra.
Euclidean geometry, on the other hand, deals with these objects and their spatial arrangement using a system of reasoning and logical deductions.
Euclidean geometry was first developed to solve surveying problems and is still used widely for this purpose today. Euclidean geometry principles are also used in architectural design and art. Some of the most interesting applications of Euclidean geometry are used to help us determine the best packing arrangement for various types of objects.
Did you know?
Euclid, the ‘Father of Geometry’ was a Greek mathematician from the third century BC. He wrote a book on geometry called the Elements which is still considered one of the most important and influential books on mathematics. The Elements also dealt with number theory, factorisation and common divisors.
Euclidean geometry is not the only kind of geometry. Spherical geometry, for example, deals with the geometry of spheres. In spherical geometry, the angles inside a triangle do not add up to [latex]\scriptsize {{180}^\circ}[/latex]. They add up to more than [latex]\scriptsize {{180}^\circ}[/latex]. How much more depends on the size and shape of the triangle. These alternative geometries are called non-Euclidean geometries.
Watch the video called “5-Sided Square” if you are interested in learning more about spherical geometry.
In this subject outcome, we will focus on a section of Euclidean geometry called circle geometry which considers the relationships between circles, triangles (three-sided figures) and quadrilaterals (four-sided figures).
Studying geometry in general and circle geometry in particular is an excellent way to help us develop and hone our logic, reasoning and argumentation skills. Being able to reason logically and express our reasons and arguments clearly and concisely is an important and valuable life skill.
Angles and lines
Many of the properties of angles and lines you will most likely be familiar with already, but we will list them all in this section for completeness.
We know that an angle is formed when two lines meet or intersect at a point (called a vertex). We measure the size of the angle between the two lines in degrees. Here is some of the basic terminology used to describe and work with angles.
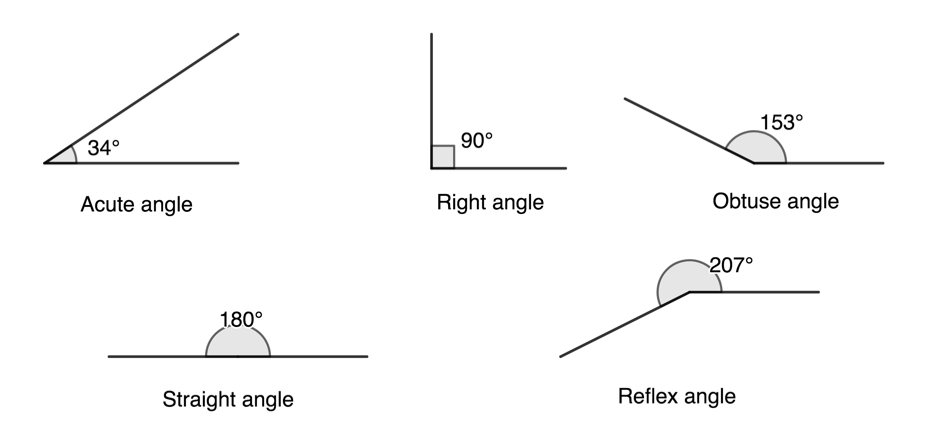
- Angles smaller than [latex]\scriptsize {{90}^\circ}[/latex] are called acute angles.
- Angles of [latex]\scriptsize {{90}^\circ}[/latex] are called right angles
- Angles between [latex]\scriptsize {{90}^\circ}[/latex] and [latex]\scriptsize {{180}^\circ}[/latex] are called obtuse angles.
- Angles of [latex]\scriptsize {{180}^\circ}[/latex] are called straight angles and are on a straight line.
- Angles between [latex]\scriptsize {{180}^\circ}[/latex] and [latex]\scriptsize {{360}^\circ}[/latex] are called reflex angles.
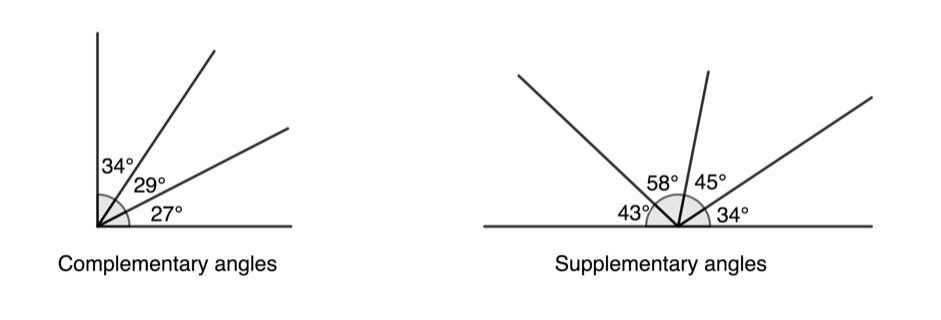
- Angles that add up to [latex]\scriptsize {{90}^\circ}[/latex] are called complementary angles.
- Angles that add up to [latex]\scriptsize {{180}^\circ}[/latex] are called supplementary angles.
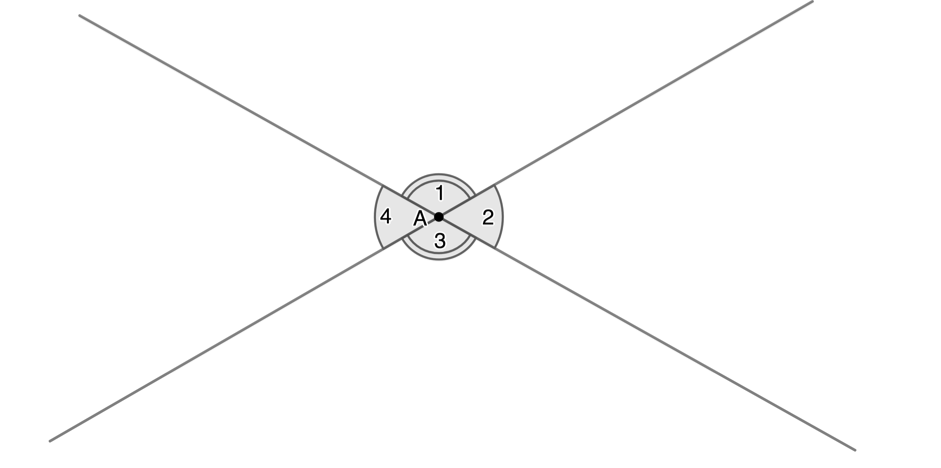
If two straight lines intersect each other, four angles are created. The vertically opposite angles in this case are equal. In other words, [latex]\scriptsize {{\hat{A}}_{1}}={{\hat{A}}_{3}}[/latex] and [latex]\scriptsize {{\hat{A}}_{2}}={{\hat{A}}_{4}}[/latex] (see figure 3).
Angles and parallel lines
Often, we need to work with the angles formed by a transversal line ([latex]\scriptsize EF[/latex]) cutting two or more other lines ([latex]\scriptsize AB[/latex] and [latex]\scriptsize BC[/latex]) (see figure 4). This situation creates a number of important angles.
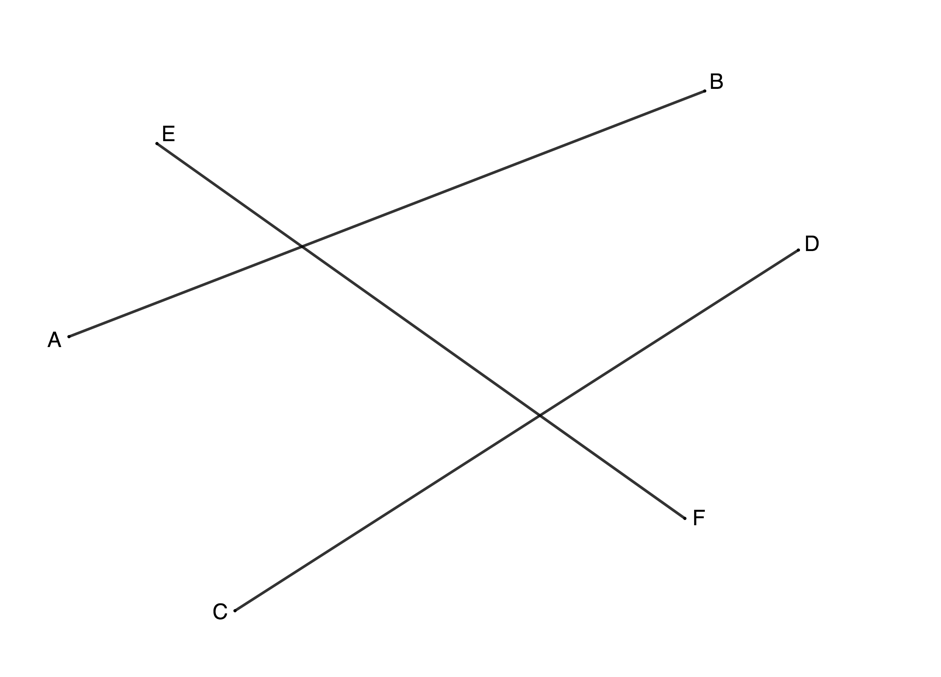
Corresponding angles are formed such as [latex]\scriptsize {{\hat{G}}_{1}}[/latex] and [latex]\scriptsize {{\hat{H}}_{1}}[/latex] (see figure 5). Corresponding angles are on the corresponding side of the lines and the same side of the transversal.
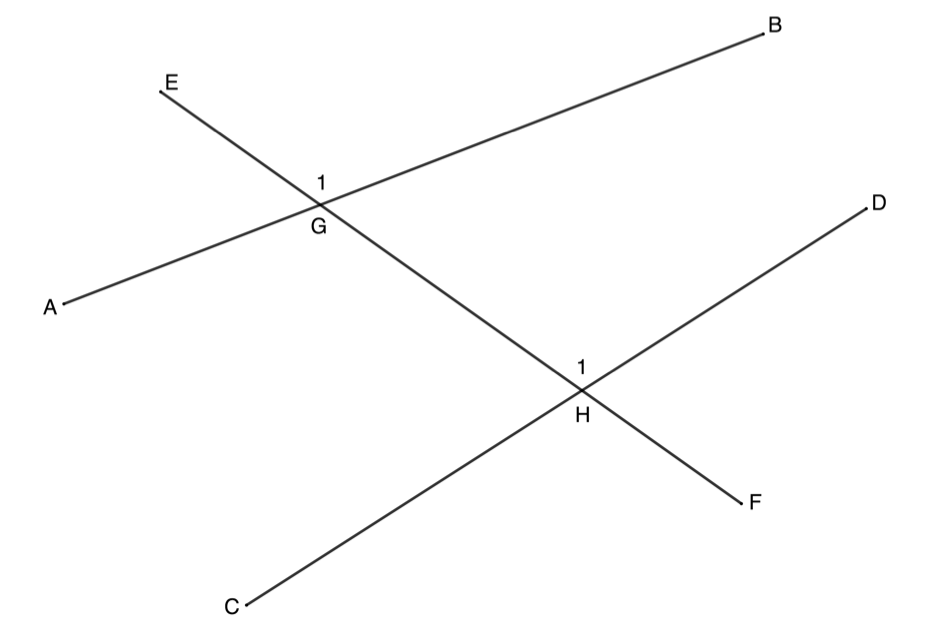
Alternate angles are formed such as [latex]\scriptsize {{\hat{G}}_{2}}[/latex] and [latex]\scriptsize {{\hat{H}}_{1}}[/latex] (see figure 6). Alternate angles lie between the lines and on opposite sides of the transversal.
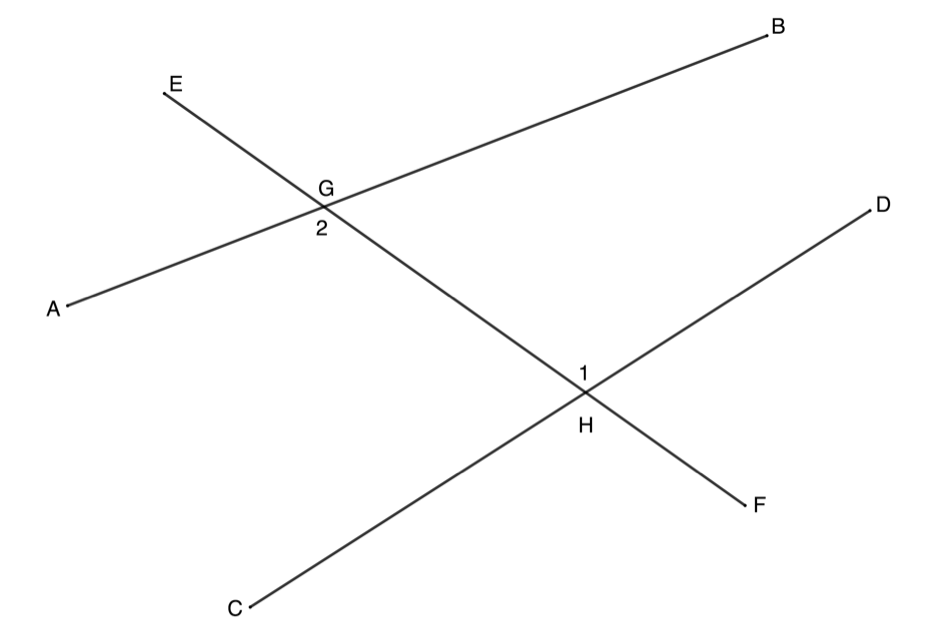
Co-interior angles are formed such as [latex]\scriptsize {{\hat{G}}_{3}}[/latex] and [latex]\scriptsize {{\hat{H}}_{1}}[/latex] (see figure 7). Co-interior angles lie between the lines and on the same side of the transversal.
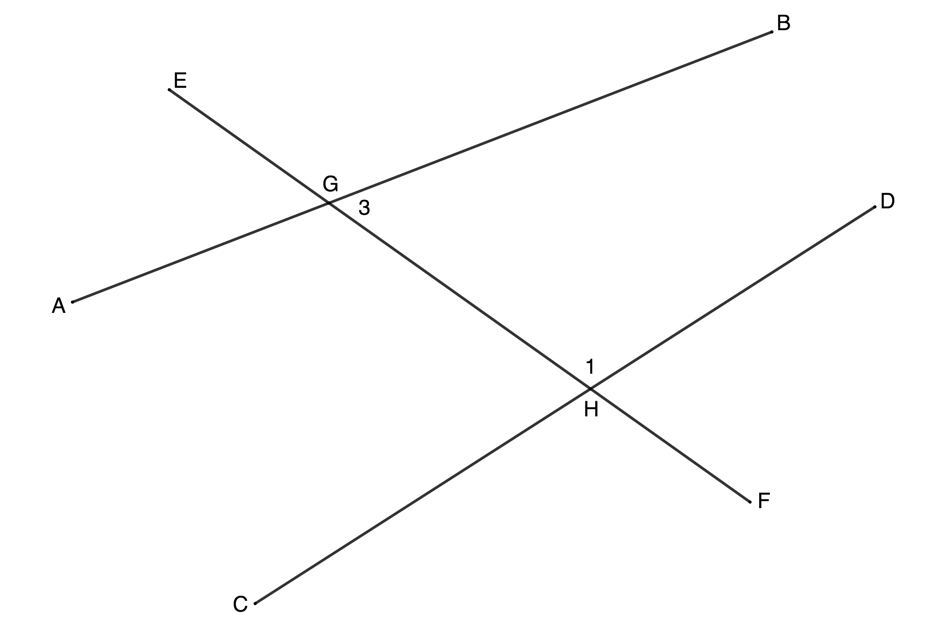
When those two (or more) lines cut by the transversal are parallel, these three angle pairs have special properties. In figure 8, [latex]\scriptsize AB\parallel CD[/latex] and so:
- the corresponding angles are equal ([latex]\scriptsize {{\hat{G}}_{1}}={{\hat{H}}_{1}}[/latex])
- the alternate angles are equal ([latex]\scriptsize {{\hat{G}}_{2}}={{\hat{H}}_{1}}[/latex])
- the co-interior angles are supplementary ([latex]\scriptsize {{\hat{G}}_{3}}+{{\hat{H}}_{1}}={{180}^\circ}[/latex]).
Note in figure 8 that we know that [latex]\scriptsize {{\hat{G}}_{1}}={{\hat{G}}_{2}}[/latex] because these angles are also vertically opposite. Also note that [latex]\scriptsize \displaystyle {{\hat{G}}_{1}}+{{\hat{G}}_{3}}={{180}^\circ}[/latex] because they are angles on the same straight line ([latex]\scriptsize EF[/latex]). Therefore, it makes sense that if [latex]\scriptsize \displaystyle {{\hat{G}}_{1}}+{{\hat{G}}_{3}}={{180}^\circ}[/latex] and [latex]\scriptsize {{\hat{G}}_{1}}={{\hat{H}}_{1}}[/latex], then [latex]\scriptsize {{\hat{G}}_{3}}+{{\hat{H}}_{1}}={{180}^\circ}[/latex].
Take note!
When two lines are cut by a transversal, corresponding, alternate and co-interior angles are always created.
If lines being cut by the transversal are parallel, then the corresponding angles are equal, the alternate angles are equal and the co-interior angles are supplementary.
By the same logic, if the corresponding angles are equal, or the alternate angles are equal or the co-interior angles are supplementary, then the lines are parallel.
Note
If you would like an excellent summary of the angles created by parallel lines, watch the video called “Angles In Parallel Lines”.
Example 1.1
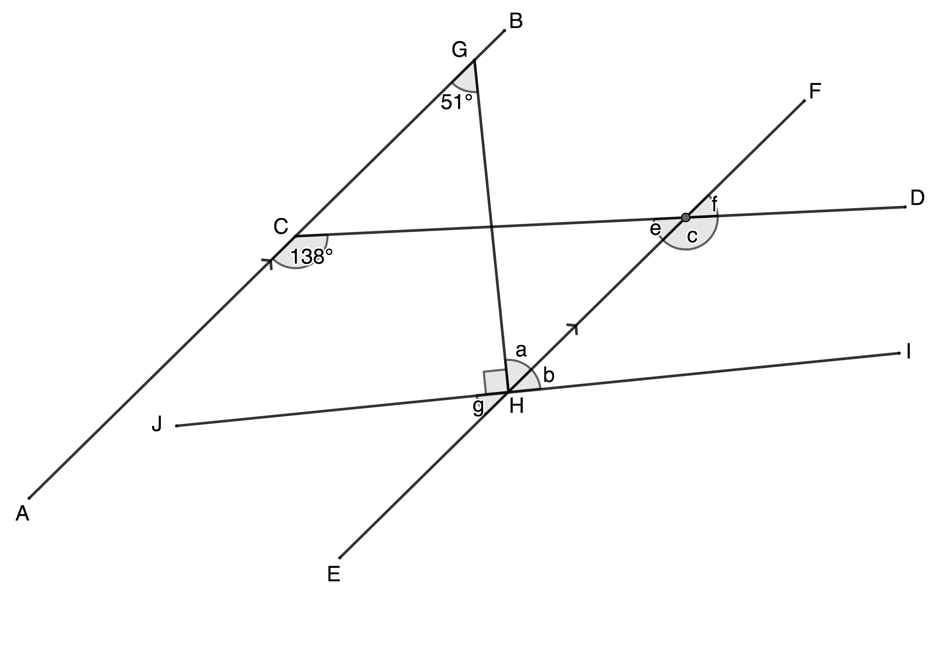
Find all the unknown angles if [latex]\scriptsize AB\parallel EF[/latex].
Solution
The most important thing when answering Euclidean geometry questions is to provide reasons for each statement you make. Remember, you are constructing a logical argument. Each step in your argument needs to have a logical reason so that the entire argument is true. If just one step is false, the entire argument falls down. Pay special attention to how the reasons for each assertion made below are provided.
We have been told that [latex]\scriptsize AB\parallel EF[/latex]. Therefore, we need to look for corresponding, alternate and co-interior angles.
[latex]\scriptsize \hat{a}={{51}^\circ}\quad \text{alt angles are equal};AB\parallel EF[/latex]
You must state which parallel lines make the alternate angles equal.
[latex]\scriptsize \begin{align*}G\hat{H}J+\hat{a}+\hat{b} & ={{180}^\circ}\quad \text{angles on a str line suppl}\\\text{But }G\hat{H}J & ={{90}^\circ}\quad \text{given}\\\therefore \hat{a}+\hat{b} & ={{90}^\circ}\\\therefore \hat{b} & ={{90}^\circ}-{{51}^\circ}={{39}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}A\hat{C}D+\hat{e} & ={{180}^\circ}\quad \text{co-int angles are supplementary; }AB\parallel EF\\\therefore \hat{e} & ={{180}^\circ}-{{138}^\circ}={{42}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}ACD & =\hat{c}\quad \text{corresp angles }=;AB\parallel EF\\\therefore \hat{c} & ={{138}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}\hat{e} & =\hat{f}\quad \text{vert opp angles }=\\\therefore \hat{f} & ={{42}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}\hat{b} & =\hat{g}\quad \text{vert opp angles }=\\\therefore \hat{g} & ={{39}^\circ}\end{align*}[/latex]
Note: You can use abbreviated words (like ‘alt’ for alternate) or the full word.
Note: Be careful. [latex]\scriptsize \hat{b}[/latex] and [latex]\scriptsize \hat{c}[/latex] are co-interior angles but [latex]\scriptsize CD[/latex] is not parallel to [latex]\scriptsize JI[/latex], therefore these co-interior angles are not supplementary.
Example 1.2
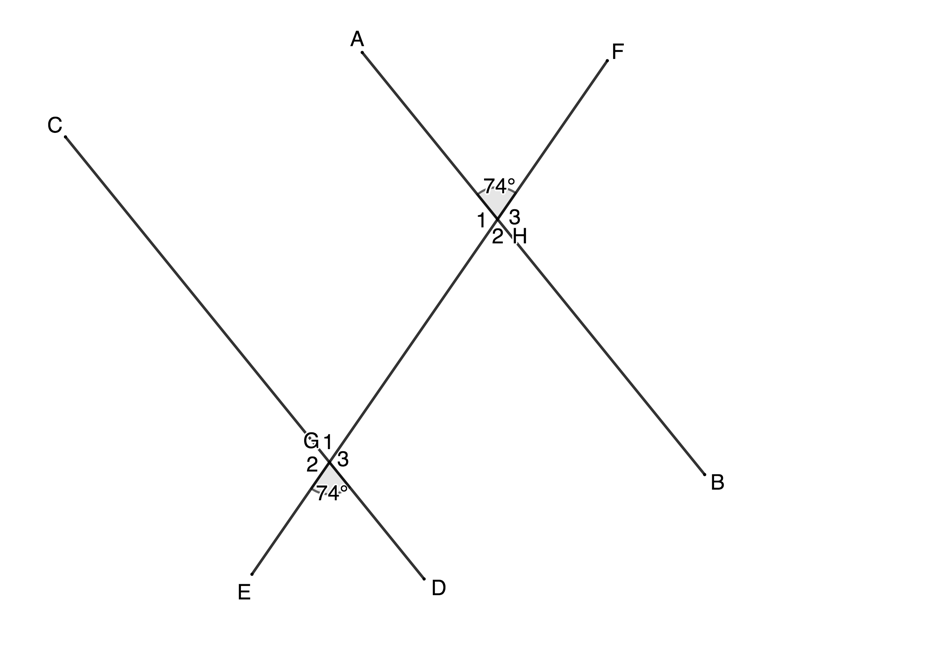
Determine if [latex]\scriptsize AB[/latex] is parallel to [latex]\scriptsize CD[/latex].
Solution
In this case, we need to prove that the lines are parallel by showing that the corresponding angles are equal, or the alternate angles are equal, or the co-interior angles are supplementary.
[latex]\scriptsize \begin{align*}{{{\hat{G}}}_{1}} & ={{74}^\circ}\quad \text{vert opp angles =}\\\therefore {{{\hat{G}}}_{1}} & =A\hat{H}F\\\therefore AB & \parallel CD\quad \text{corresp angles }=\end{align*}[/latex]
Note: This is just one way to prove that [latex]\scriptsize AB\parallel CD[/latex]. We could also have shown that, for example, the alternate angles [latex]\scriptsize {{\hat{G}}_{1}}[/latex] and [latex]\scriptsize {{\hat{H}}_{2}}[/latex] are equal or that the co-interior angles [latex]\scriptsize {{\hat{G}}_{1}}[/latex] and [latex]\scriptsize {{\hat{H}}_{1}}[/latex] are supplementary.
Exercise 1.1
Question 1 adapted from Everything Maths Grade 10 Exercise 7 – 1 question 2
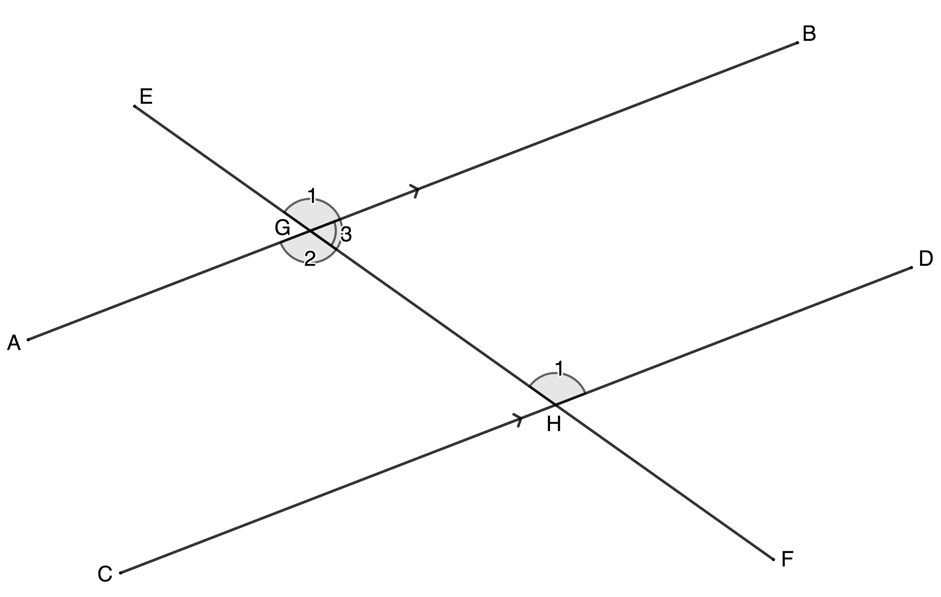
- Find all the unknown angles in the figure below:
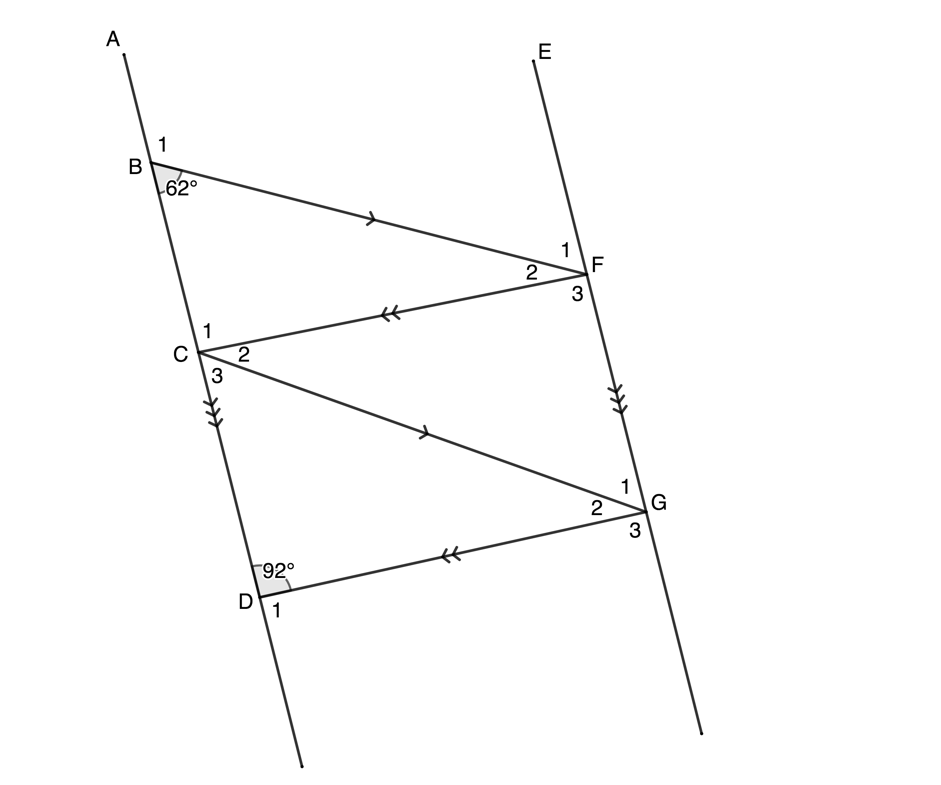
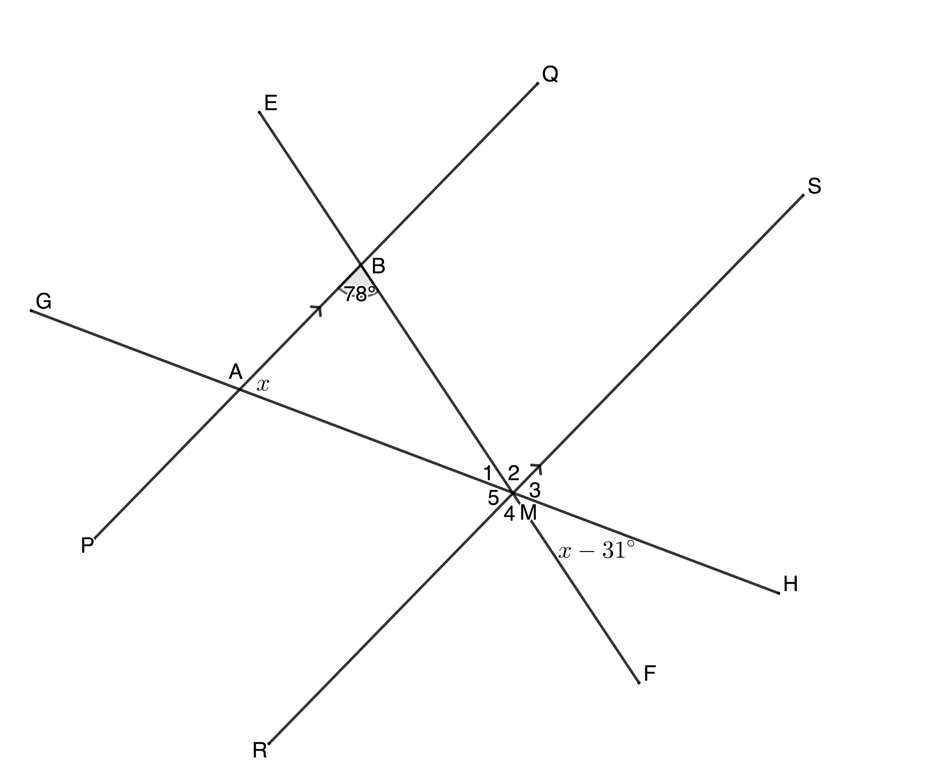
- Determine the value of [latex]\scriptsize x[/latex] in the following diagram:
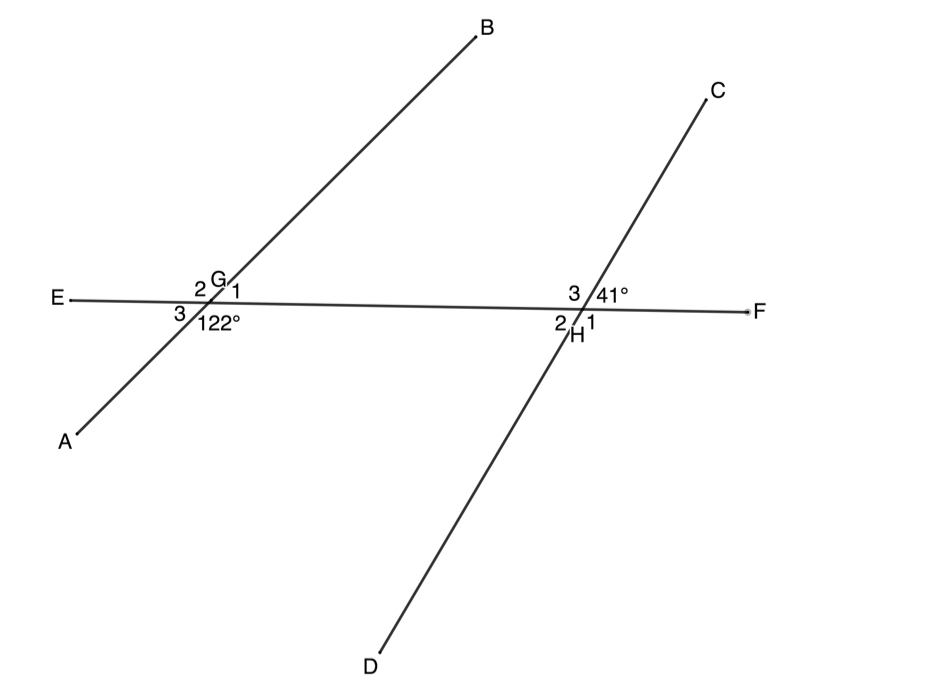
- Determine if [latex]\scriptsize AB[/latex] and [latex]\scriptsize CD[/latex] are parallel:
The full solutions are at the end of the unit.
Angles in triangles
By this stage, you should be very familiar with triangles. There are four types of triangles. These and their characteristics are summarised in figure 9.
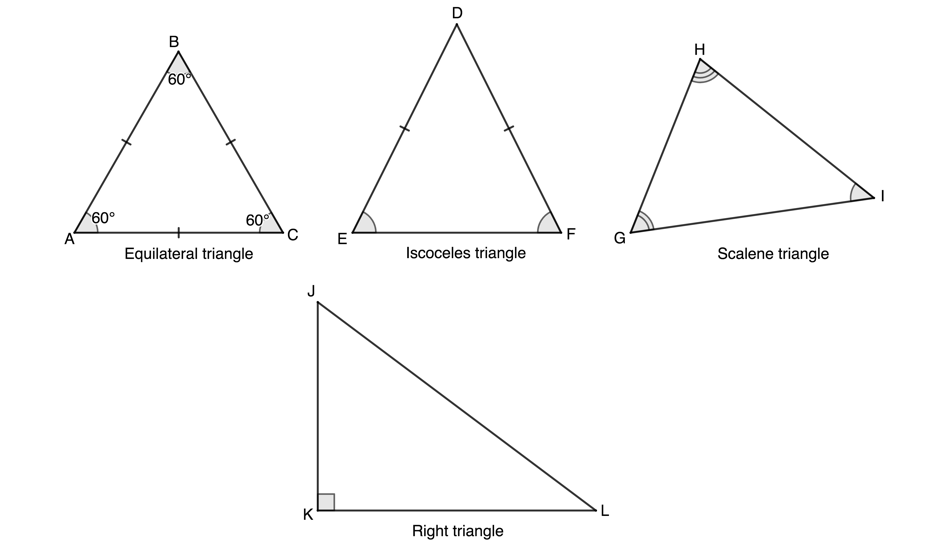
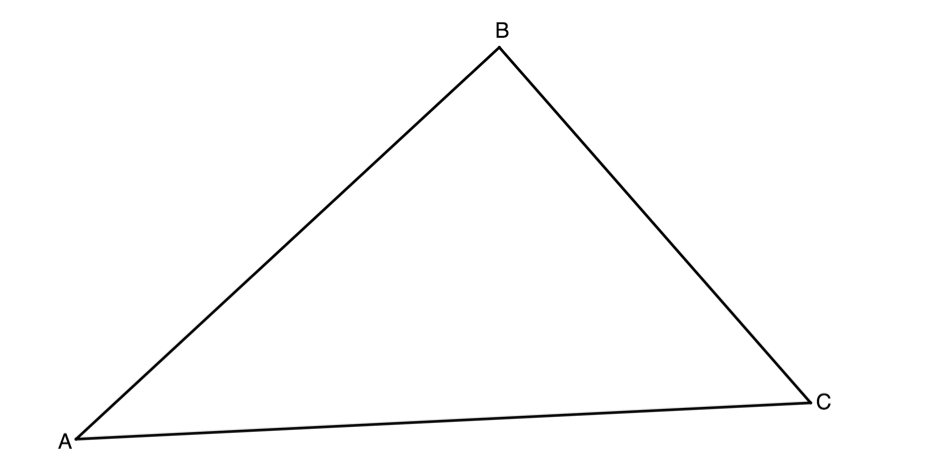
We know that the sum of the interior angles of a triangle is [latex]\scriptsize {{180}^\circ}[/latex]. In other words, in figure 10 [latex]\scriptsize \hat{A}+\hat{B}+\hat{C}={{180}^\circ}[/latex]. The interior angles of a triangle are supplementary.
This is why all the angles in an equilateral triangle are [latex]\scriptsize {{60}^\circ}[/latex] ([latex]\scriptsize \displaystyle \frac{{{{{180}}^\circ}}}{3}={{60}^\circ}[/latex]).
But we also know that the angles on a straight line are supplementary. Therefore, what can we say about angles [latex]\scriptsize \hat{A}[/latex], [latex]\scriptsize \hat{B}[/latex] and [latex]\scriptsize {{\hat{C}}_{2}}[/latex] in figure 11?
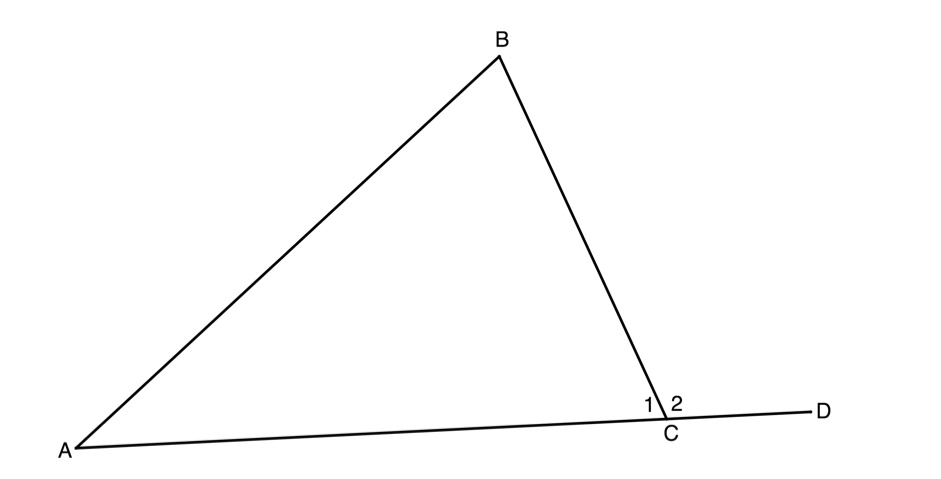
[latex]\scriptsize \begin{align*}\hat{A}+\hat{B}+{{{\hat{C}}}_{1}}&={{180}^\circ}\quad \text{int angles of }\Delta \text{ suppl}\\\text{But }{{{\hat{C}}}_{1}}+{{{\hat{C}}}_{2}}&={{180}^\circ}\quad \text{angles on str line suppl}\\\therefore {{{\hat{C}}}_{2}}&=\hat{A}+\hat{B}\end{align*}[/latex]
We say that the exterior angle of a triangle (the angle made by extending any of the sides of the triangle) is equal to the sum of the two opposite interior angles (ext angle of [latex]\scriptsize \Delta =[/latex] opp int angles).
Exercise 1.2
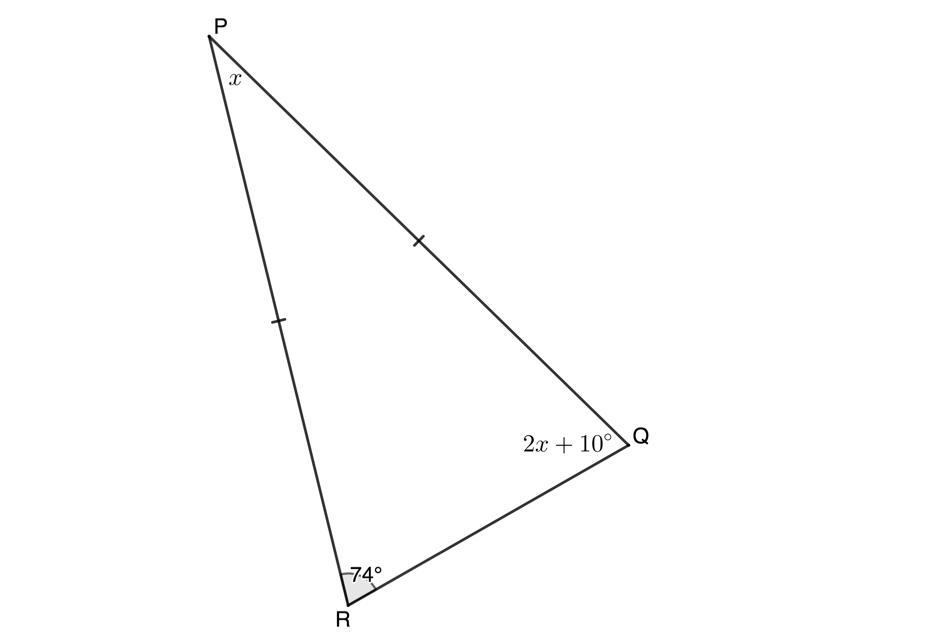
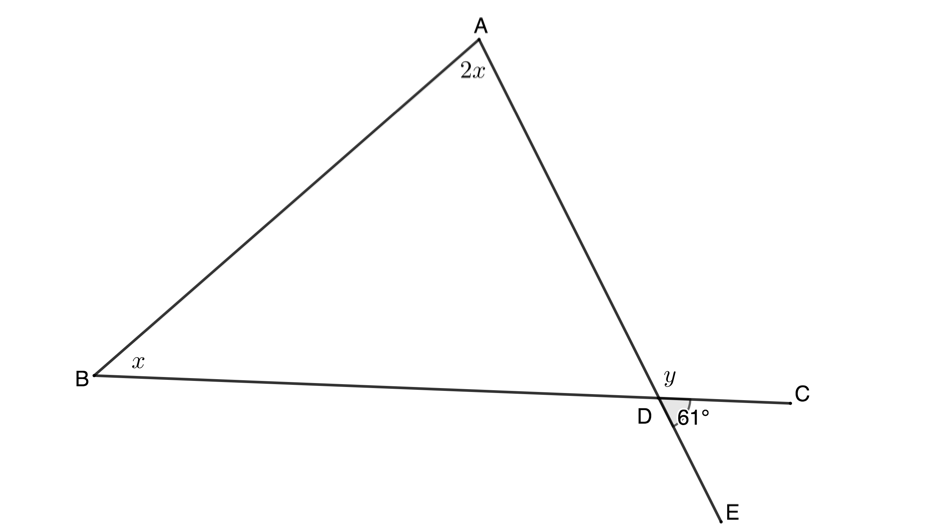
Calculate the unknown variables in each of the following figures:
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- The different kinds of angles are acute, right, obtuse, straight, and reflex.
- Complementary angles add up to [latex]\scriptsize {{90}^\circ}[/latex].
- Supplementary angles add up to [latex]\scriptsize {{180}^\circ}[/latex].
- That when lines cut by a transversal are parallel, the alternate angles are equal, the corresponding angles are equal and the co-interior angles are supplementary.
- The different kinds of triangles are equilateral, isosceles, scalene and right.
- That the interior angles of a triangle add up to [latex]\scriptsize {{180}^\circ}[/latex].
- That the exterior angle of a triangle is equal to the sum of the opposite interior angles.
Unit 1: Assessment
Suggested time to complete: 25 minutes
Question 1 adapted from NC(V) Mathematics Level 4 Paper 2 November 2016 question 1.1
- In the diagram given below, [latex]\scriptsize AB\parallel CD[/latex] and [latex]\scriptsize EFGH[/latex] is a transversal with [latex]\scriptsize F[/latex] on [latex]\scriptsize AB[/latex] and [latex]\scriptsize G[/latex] on [latex]\scriptsize CD[/latex]. [latex]\scriptsize F\hat{G}C=2x+{{22}^\circ}[/latex] and [latex]\scriptsize H\hat{G}D=3x-{{20}^\circ}[/latex].
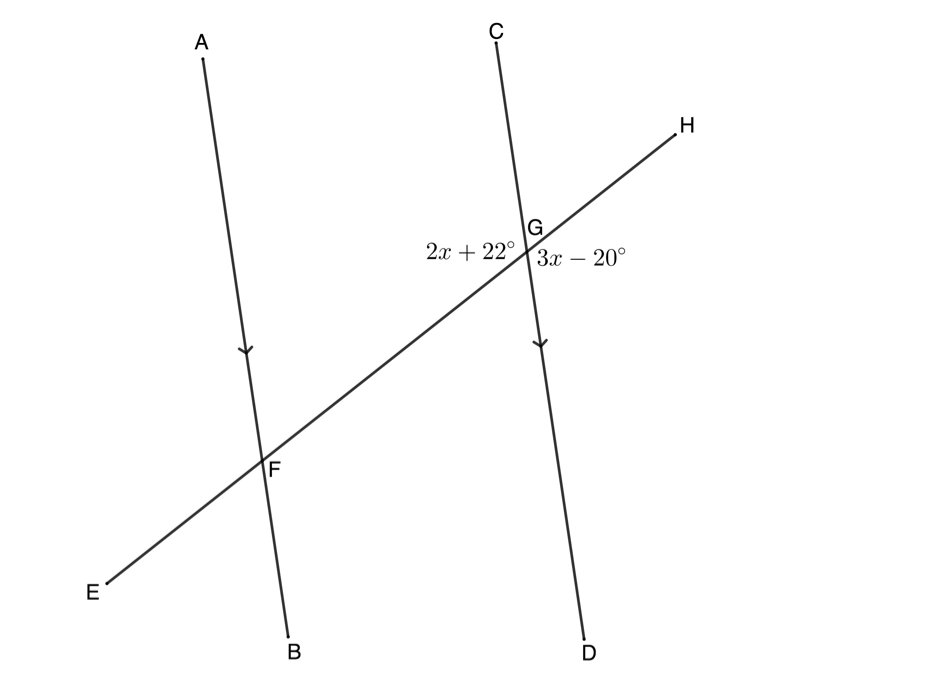
- Determine the value of [latex]\scriptsize x[/latex].
- Determine the magnitude of [latex]\scriptsize E\hat{F}B[/latex].
Question 2 adapted from NC(V) Mathematics Level 4 Paper 2 November 2015 question 1.1
- In the diagram below [latex]\scriptsize PQ\parallel RS\parallel TU\parallel VW[/latex]. [latex]\scriptsize PR[/latex], [latex]\scriptsize SU[/latex] and [latex]\scriptsize TW[/latex] are drawn and [latex]\scriptsize MN\parallel PR[/latex]. Also, [latex]\scriptsize \hat{P}={{105}^\circ}[/latex], [latex]\scriptsize \hat{S}={{76}^\circ}[/latex] and [latex]\scriptsize \hat{T}={{29}^\circ}[/latex].
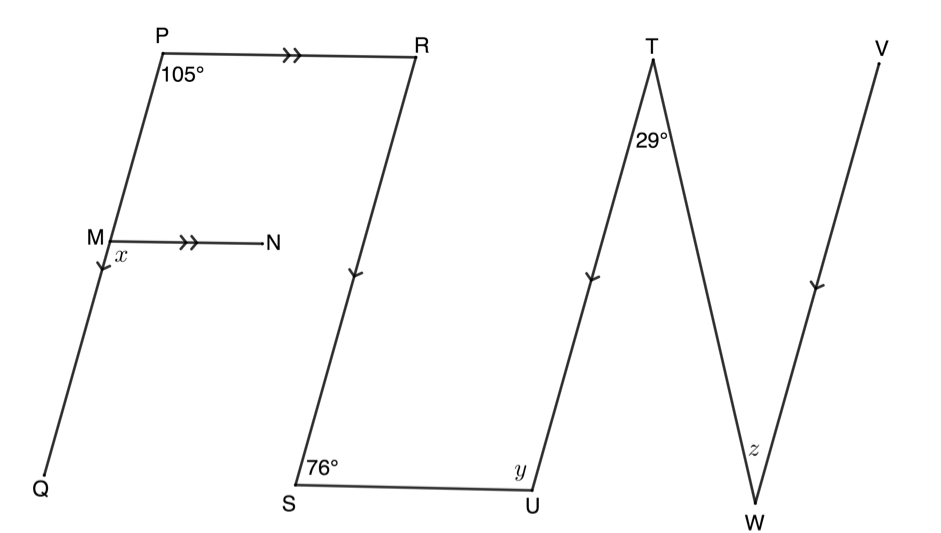
Determine, with reasons, the sizes of [latex]\scriptsize x[/latex], [latex]\scriptsize y[/latex] and [latex]\scriptsize z[/latex].
Question 3 adapted from NC(V) Mathematics Level 4 Paper 2 November 2014 question 1.2
- In the diagram below, parallel lines [latex]\scriptsize AB[/latex] and [latex]\scriptsize CD[/latex] are cut by two transversals [latex]\scriptsize SPQ[/latex] and [latex]\scriptsize TPR[/latex]. Both transversals intersect [latex]\scriptsize CD[/latex] at [latex]\scriptsize P[/latex]. If [latex]\scriptsize P\hat{R}Q=y[/latex], [latex]\scriptsize P\hat{Q}R={{60}^\circ}[/latex] and [latex]\scriptsize S\hat{P}T=y-{{20}^\circ}[/latex], determine the value of [latex]\scriptsize y[/latex].
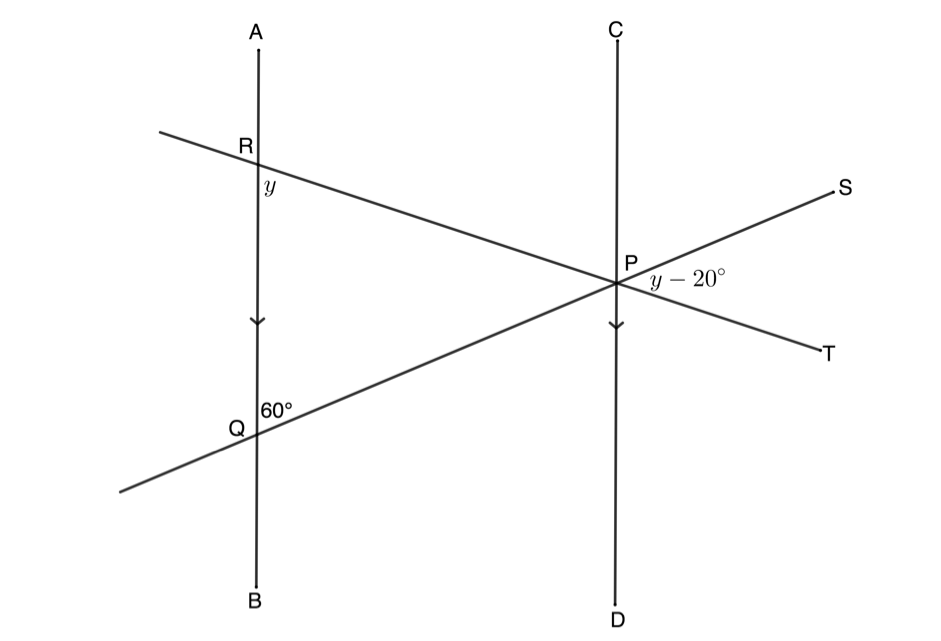
Question 4 adapted from NC(V) Mathematics Level 4 Paper 2 November 2013 question 1.1
- In the figure below, [latex]\scriptsize AC\parallel EG[/latex], [latex]\scriptsize BD=CD[/latex] and [latex]\scriptsize C\hat{B}D={{50}^\circ}[/latex].
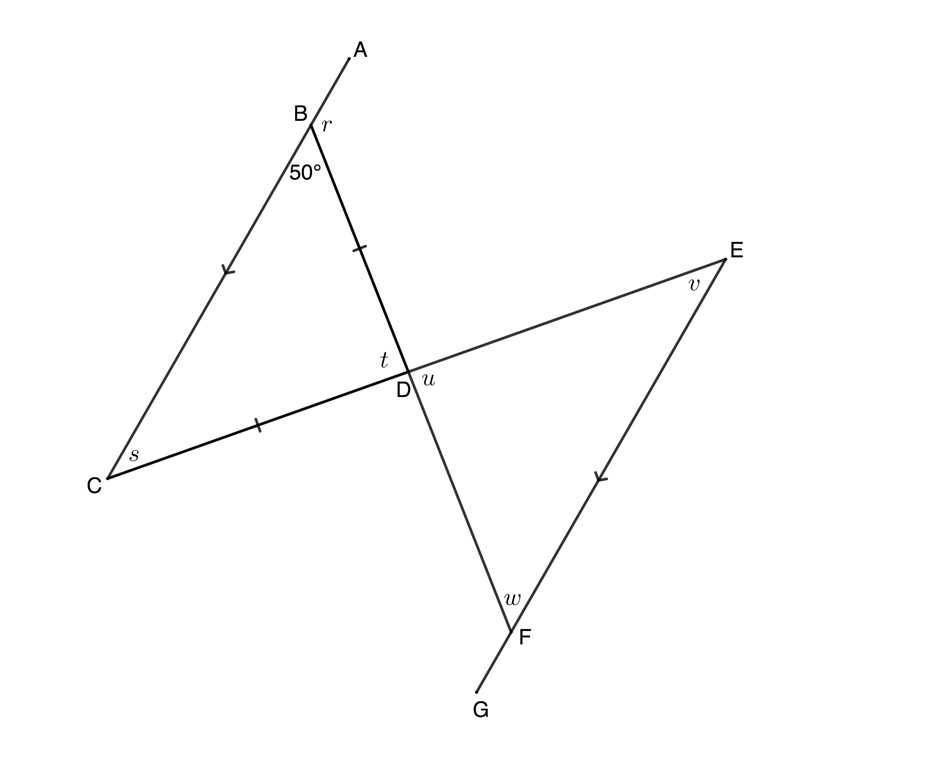
Determine, giving reasons, the value of [latex]\scriptsize r[/latex], [latex]\scriptsize s[/latex], [latex]\scriptsize t[/latex], [latex]\scriptsize u[/latex], [latex]\scriptsize v[/latex] and [latex]\scriptsize w[/latex]. - In the diagram, [latex]\scriptsize AB\parallel CD[/latex]. Calculate the sizes of [latex]\scriptsize F\hat{H}G[/latex], [latex]\scriptsize \hat{F}[/latex], [latex]\scriptsize \hat{C}[/latex] and [latex]\scriptsize \hat{D}[/latex]. Give reasons for your answers.
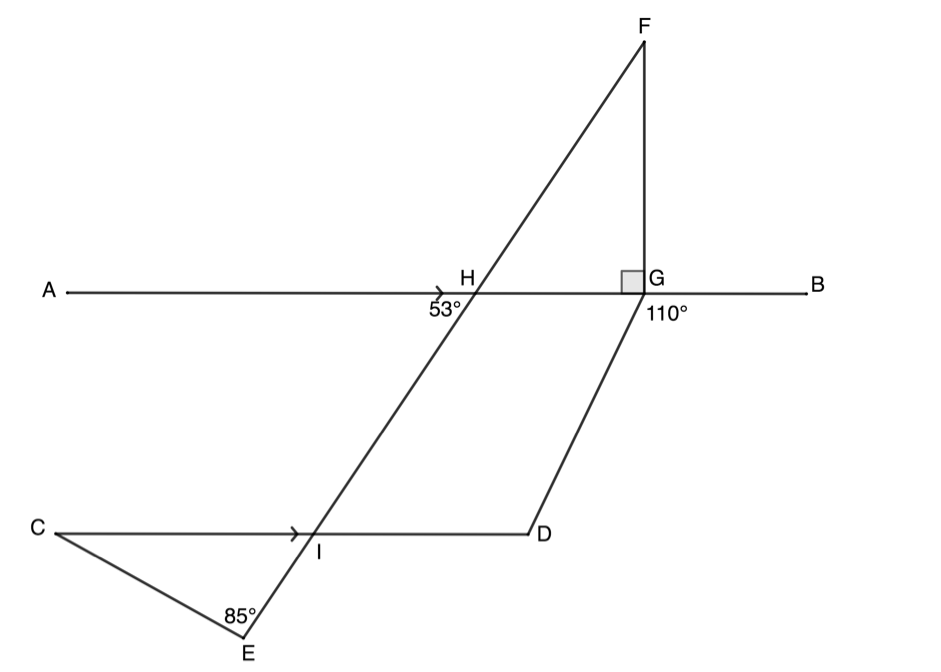
The full solutions are at the end of the unit.
Unit 1: Solutions
Exercise 1.1
- .
[latex]\scriptsize {{\hat{D}}_{1}}={{180}^\circ}-{{92}^\circ}={{88}^\circ}\quad \text{angles on a str line suppl}[/latex]
[latex]\scriptsize {{\hat{B}}_{1}}={{180}^\circ}-{{62}^\circ}={{118}^\circ}\quad \text{angles on a str line suppl}[/latex]
[latex]\scriptsize {{\hat{F}}_{1}}={{62}^\circ}\quad \text{alt angles }=;AD\parallel EG[/latex]
[latex]\scriptsize \begin{align*}{{{\hat{F}}}_{1}} & ={{{\hat{G}}}_{1}}\quad \text{corresp angles }=;BF\parallel CG\\\therefore {{{\hat{G}}}_{1}} & ={{62}^\circ}\end{align*}[/latex]
[latex]\scriptsize {{\hat{C}}_{1}}={{92}^\circ}\quad \text{corresp angles }=;CF\parallel DG[/latex]
[latex]\scriptsize \begin{align*}{{{\hat{F}}}_{3}} & ={{{\hat{C}}}_{1}}\quad \text{alt angles }=;AD\parallel EG\\\therefore {{{\hat{F}}}_{3}} & ={{92}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{{\hat{C}}}_{1}}+{{{\hat{F}}}_{1}}+{{{\hat{F}}}_{2}} & ={{180}^\circ}\quad \text{co-int angles suppl; }AD\parallel EG\\\therefore {{{\hat{F}}}_{2}} & ={{180}^\circ}-{{62}^\circ}-{{92}^\circ}={{26}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{{\hat{C}}}_{2}} & ={{{\hat{F}}}_{2}}\quad \text{alt angles }=;BF\parallel CG\\\therefore {{{\hat{C}}}_{2}} & ={{26}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{{\hat{G}}}_{2}} & ={{{\hat{C}}}_{2}}\quad \text{alt angles }=;BF\parallel CG\\\therefore {{{\hat{G}}}_{2}} & ={{26}^\circ}\end{align*}[/latex]
[latex]\scriptsize {{\hat{C}}_{3}}=C\hat{B}F={{62}^\circ}\quad \text{corresp angles }=;BF\parallel CG[/latex]
[latex]\scriptsize {{\hat{G}}_{3}}={{92}^\circ}\quad \text{alt angles }=;AD\parallel EG[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}{{{\hat{M}}}_{5}} & =x\quad \text{alt angles }=;PQ\parallel RS\\{{{\hat{M}}}_{2}} & ={{78}^\circ}\quad \text{alt angles }=;PQ\parallel RS\\{{{\hat{M}}}_{1}} & =x-{{31}^\circ}\quad \text{vert opp angles }=\\{{{\hat{M}}}_{1}}+{{{\hat{M}}}_{2}}+{{{\hat{M}}}_{5}} & ={{180}^\circ}\quad \text{angles on str line suppl}\\\therefore x-{{31}^\circ}+{{78}^\circ}+x & ={{180}^\circ}\\\therefore 2x & ={{133}^\circ}\\\therefore x & ={{66.5}^\circ}\end{align*}[/latex] - .
Note: You cannot make a conclusion based on what the diagram looks like. You must work with the angles to see if they provide a condition for the lines being parallel or not.
[latex]\scriptsize \begin{align*}{{{\hat{G}}}_{1}}+{{122}^\circ} & ={{180}^\circ}\quad \text{angles on str line suppl}\\\therefore {{{\hat{G}}}_{1}} & ={{180}^\circ}-{{122}^\circ}={{58}^\circ}\\\therefore {{{\hat{G}}}_{1}} & \ne {{41}^\circ}\\\therefore \text{corresp } & \text{angles not equal}\\\therefore AB\text{ not } & \text{parallel to }CD\end{align*}[/latex]
Exercise 1.2
- .
[latex]\scriptsize \begin{align*}2x+{{10}^\circ} & ={{74}^\circ}\quad =\text{ sides }=\text{ angles}\\\therefore 2x & ={{64}^\circ}\\\therefore x & ={{32}^\circ}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}y & ={{180}^\circ}-{{61}^\circ}\quad \text{angles on str line suppl}\\\therefore y & ={{119}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}x+2x & =y={{119}^\circ}\quad \text{ext angle of }\Delta =\text{ opp int angles}\\\therefore 3x & ={{119}^\circ}\\\therefore x & ={{39.67}^\circ}\end{align*}[/latex] - .
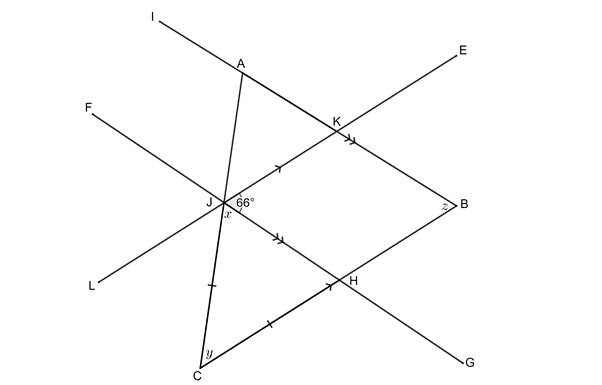
[latex]\scriptsize \begin{align*}x+C\hat{H}J+y & ={{180}^\circ}\quad \text{angles in }\Delta \text{ suppl}\\\therefore y & ={{180}^\circ}-2\times {{66}^\circ}\\\therefore y & ={{48}^\circ}\end{align*}[/latex]
.
[latex]\scriptsize \displaystyle \begin{align*}F\hat{J}A & =x={{66}^\circ}\quad \text{vert opp angles }=\\J\hat{A}K & ={{66}^\circ}\quad \text{alt angles }=;FG\parallel HB\\J\hat{A}K+z+y & ={{180}^\circ}\quad \text{angles in }\Delta \text{ABC suppl}\\\therefore z & ={{180}^\circ}-{{66}^\circ}-{{48}^\circ}={{66}^\circ}\end{align*}[/latex]
Unit 1: Assessment
- .
- .
[latex]\scriptsize \begin{align*}C\hat{G}F & =H\hat{G}D\quad \text{vert opp angles }=\\\therefore 2x+{{22}^\circ} & =3x-{{20}^\circ}\\\therefore x & ={{42}^\circ}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}CGF+AFG&=180^\circ&&\text{co-int angles suppl; }AB\parallel CD\\ \therefore AFG&=180^\circ-(2\times 42^\circ + 22^\circ)\\ \therefore AFG&=180^\circ-106^\circ=74^\circ\\ \text{But }AFG&=EFB&&\text{vert opp angles =}\\\therefore EFB&=74^\circ \end{align*}[/latex]
- .
- [latex]\scriptsize x={{105}^\circ}\quad \text{corresp angles }=;PR\parallel MN[/latex]
[latex]\scriptsize y={{180}^\circ}-{{76}^\circ}={{104}^\circ}\quad \text{co-int angles suppl};RS\parallel TU[/latex]
[latex]\scriptsize z={{29}^\circ}\quad \text{alt angles }=;TU\parallel VW[/latex] - .
[latex]\scriptsize \begin{align*}Q\hat{P}R & =y-{{20}^\circ}\quad \text{vert opp angles }=\\Q\hat{P}R+P\hat{R}Q+R\hat{Q}P & ={{180}^\circ}\quad \text{angles in }\Delta \text{ suppl}\\\therefore y-{{20}^\circ}+y+{{60}^\circ} & ={{180}^\circ}\\\therefore 2y & ={{140}^\circ}\\\therefore y & ={{70}^\circ}\end{align*}[/latex] - [latex]\scriptsize r={{180}^\circ}-{{50}^\circ}={{130}^\circ}\quad \text{angles in str line suppl}[/latex]
[latex]\scriptsize s={{50}^\circ}\quad \text{equal sides equal angles}[/latex]
[latex]\scriptsize \begin{align*}t+s+{{50}^\circ} & ={{180}^\circ}\quad \text{angles in }\Delta \text{ suppl}\\\therefore t & ={{180}^\circ}-{{50}^\circ}-{{50}^\circ}={{80}^\circ}\end{align*}[/latex]
OR
[latex]\scriptsize \begin{align*}r & =s+t\quad \text{ext angle of }\Delta \text{ }=\text{ opp int angles}\\\therefore t & ={{130}^\circ}-{{50}^\circ}={{80}^\circ}\end{align*}[/latex]
[latex]\scriptsize u={{80}^\circ}\quad \text{vert opp angles }=[/latex]
[latex]\scriptsize \begin{align*}v & =s\quad \text{alt angles }=;AC\parallel EG\\\therefore v & ={{50}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}w & =C\hat{B}D\quad \text{alt angles }=;AC\parallel EG\\\therefore w & ={{50}^\circ}\end{align*}[/latex] - [latex]\scriptsize F\hat{H}G={{53}^\circ}\quad \text{vert opp angles }=[/latex]
[latex]\scriptsize \begin{align*}\hat{F}+F\hat{H}G+F\hat{G}H & ={{180}^\circ}\quad \text{angles in }\Delta \text{ suppl}\\\therefore \hat{F} & ={{180}^\circ}-{{53}^\circ}-{{90}^\circ}={{37}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}H\hat{I}D & ={{53}^\circ}\quad \text{alt angles }=;AB\parallel CD\\\therefore C\hat{I}E & ={{53}^\circ}\quad \text{vert opp angles }=\\\therefore \hat{C} & ={{180}^\circ}-{{85}^\circ}-{{53}^\circ}\quad \text{angles in }\Delta \text{ suppl}\\\therefore \hat{C} & ={{42}^\circ}\end{align*}[/latex]
[latex]\scriptsize D={{110}^\circ}\quad \text{alt angles }=;AB\parallel CD[/latex]
Media Attributions
- figure1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure6 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure7 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure8 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example1.1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example1.2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure9 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure10 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure11 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.2 Q1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.2 Q2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.2 Q3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license