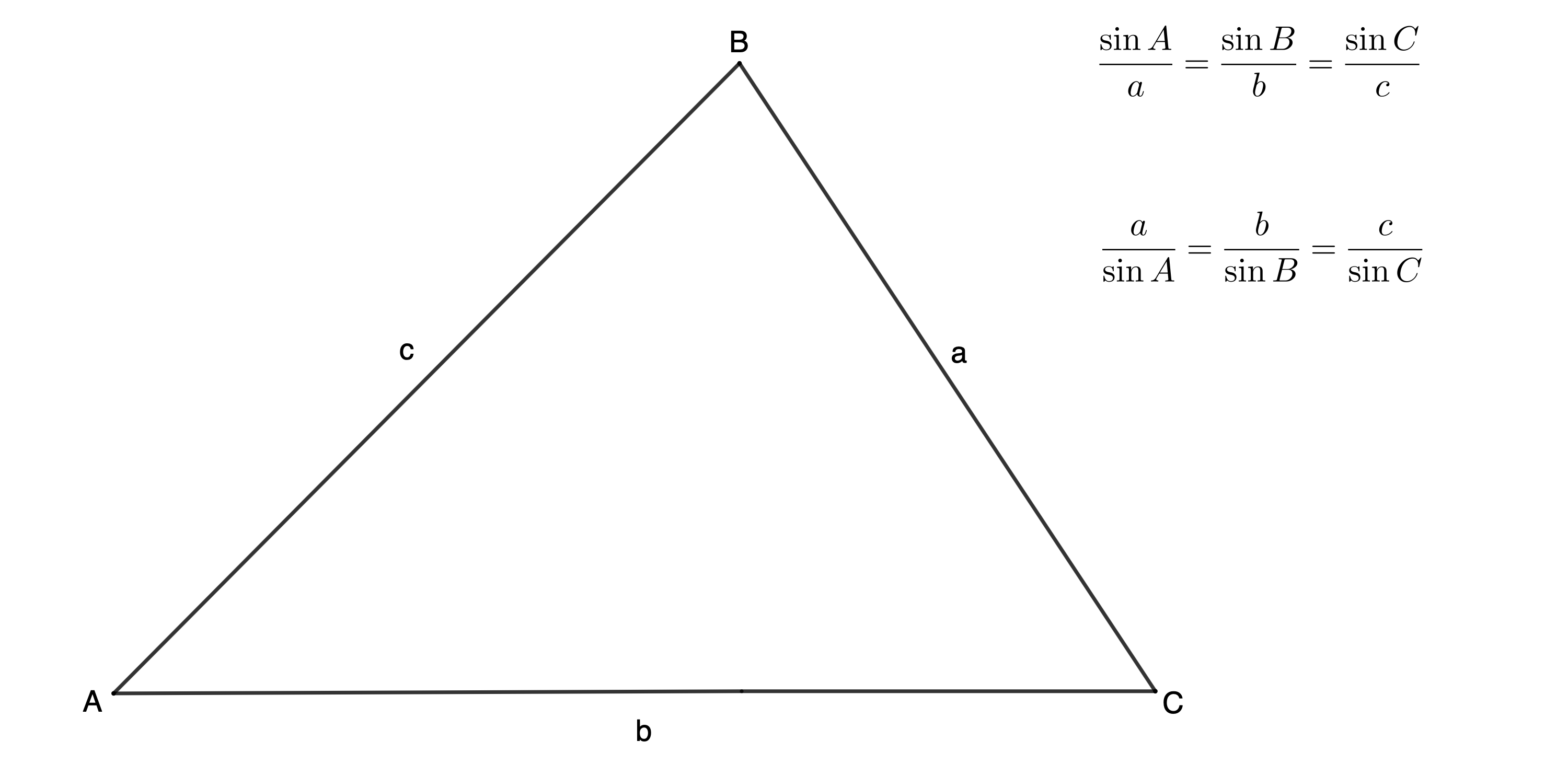
Space, shape and measurement: Solve problems by constructing and interpreting trigonometric models
Unit 3: Solve 2-D and 3-D trigonometry problems using sine and cosine rules
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Apply the sine rule correctly to solve 2-D and 3-D problems.
- Apply the cosine rule correctly to solve 2-D and 3-D problems.
What you should know
Before you start this unit, make sure you can:
- Determine the sides and angles in a right-angled triangle using the three basic trigonometric ratios. Refer to level 2 subject outcome 3.6 units 1 and 2 if you need help with this.
- Use the reduction formulae to simplify trigonometric ratios. Refer to level 3 subject outcome 3.3 units 1 and 2 if you need help with this.
- State and use the sine rule to solve 2-D problems. Refer to level 3 subject outcome 3.3 units 6 and 8 if you need help with this.
- State and use the cosine rule to solve 2-D problems. Refer to level 3 subject outcome 3.3 units 7 and 8 if you need help with this.
- State and use the compound and double angle formulae. Refer to unit 1 of this subject outcome if you need help with this.
Introduction
We learnt about the sine rule and the cosine rule in level 3 subject outcome 3.3 units 6 and 7. Remember that these rules give us a way to find the lengths of unknown sides and the sizes of unknown angles in non-right-angled triangles.
You should revise level 3 subject outcome 3.3 units 6, 7 and 8 before continuing.
Revise the sine and cosine rules
Before we learn anything new, let us revise what we already know.
Take note!
Use the sine rule if:
- no right angle is given
- two sides and an angle are given (not the included angle)
- two angles and a side are given.
Use the cosine rule if:
- no right angle is given
- two sides and the included angle are given
- three sides are given.
The difference between level 3 and level 4 is that we will use these rules to solve problems in two and three dimensions.
Revise using the sine and cosine rules to solve 2-D problems by completing the following exercise.
Exercise 3.1
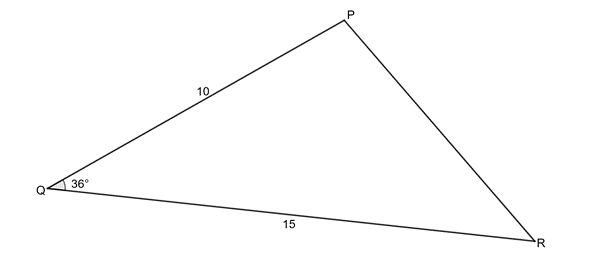
- In [latex]\scriptsize \Delta PQR[/latex], [latex]\scriptsize \hat{Q}={{36}^\circ}[/latex], [latex]\scriptsize p=15[/latex] and [latex]\scriptsize r=10[/latex]. Solve the triangle:
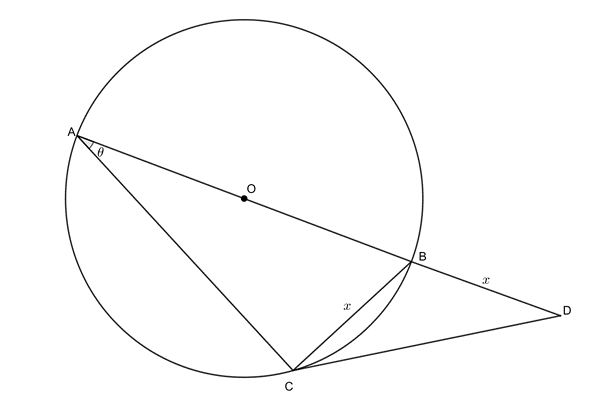
- In the diagram below, [latex]\scriptsize ABD[/latex] is a straight line through the centre of the circle. [latex]\scriptsize BD=BC=x[/latex] and [latex]\scriptsize B\hat{A}C=\theta[/latex]. Show that [latex]\scriptsize CD=2{{x}^{2}}(1+\sin \theta )[/latex].
Question 3 adapted from Everything Maths Grade 12 Exercise 4-5 question 1
- In the diagram below, [latex]\scriptsize O[/latex] is the centre of the semi-circle [latex]\scriptsize BAE[/latex]:

- Find [latex]\scriptsize A\hat{O}C[/latex] in terms of [latex]\scriptsize \theta[/latex].
- In [latex]\scriptsize \Delta ABE[/latex], determine an expression for [latex]\scriptsize \cos \theta[/latex].
- In [latex]\scriptsize \Delta ACE[/latex], determine an expression for [latex]\scriptsize \sin \theta[/latex].
- In [latex]\scriptsize \Delta ACO[/latex], determine an expression for [latex]\scriptsize \sin 2\theta[/latex].
- Use the results from the previous questions to show that [latex]\scriptsize \sin 2\theta =2\sin \theta \cos \theta[/latex].
- Two vertical towers [latex]\scriptsize AC[/latex] and [latex]\scriptsize BD[/latex] are [latex]\scriptsize \text{7 m}[/latex] and [latex]\scriptsize \text{10 m}[/latex] high, respectively. Point [latex]\scriptsize E[/latex] lies between the two towers. The angle of elevation from [latex]\scriptsize E[/latex] to [latex]\scriptsize C[/latex] is [latex]\scriptsize {{35}^\circ}[/latex]and [latex]\scriptsize E[/latex] to [latex]\scriptsize D[/latex] is [latex]\scriptsize {{55}^\circ}[/latex]. A cable is needed to connect [latex]\scriptsize C[/latex] and [latex]\scriptsize D[/latex].
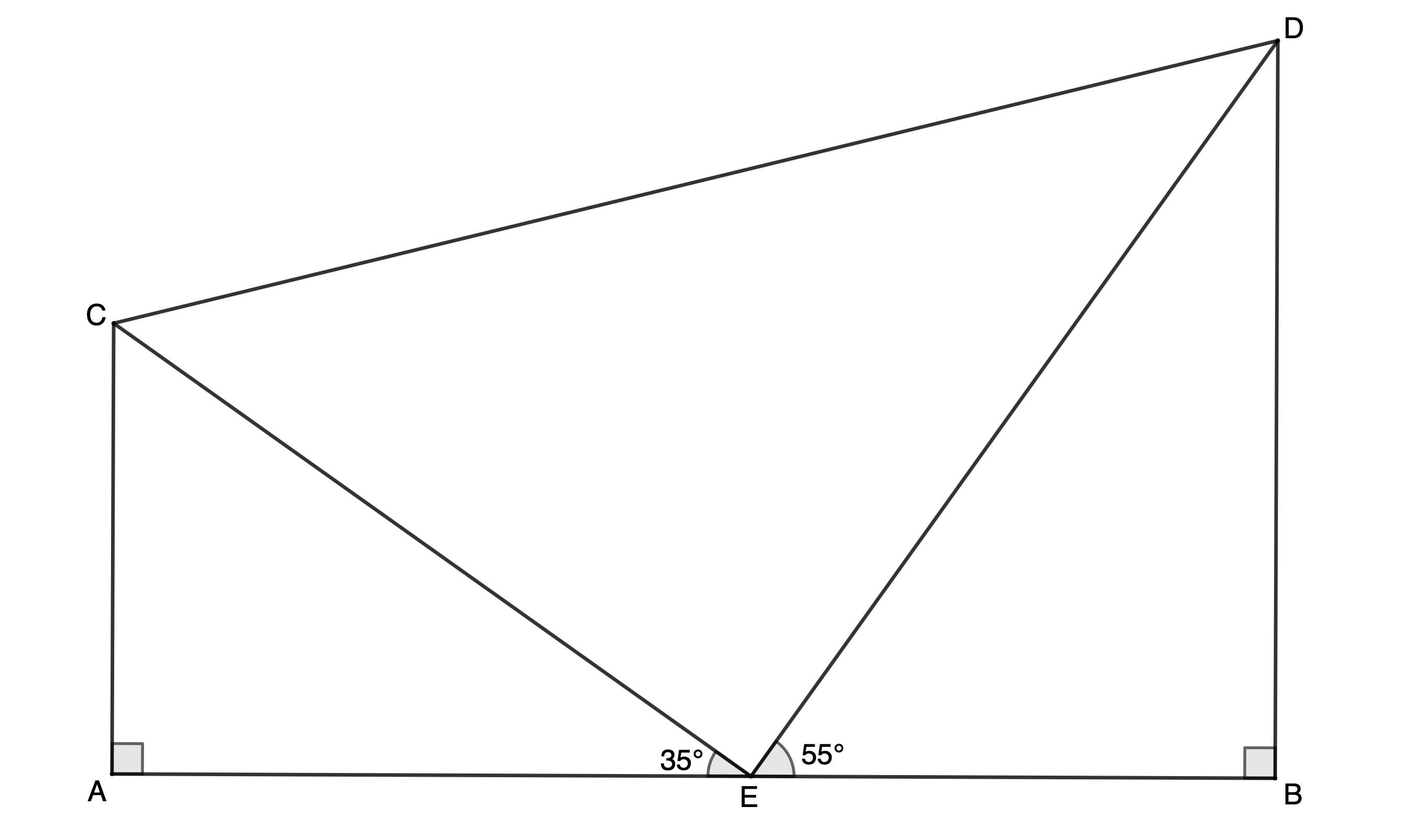
- Determine the minimum length of cable needed to connect [latex]\scriptsize C[/latex] and [latex]\scriptsize D[/latex] (to the nearest metre).
- How far apart are the bases of the two towers (to the nearest metre)?
The full solutions are at the end of the unit.
Problems in three dimensions
As we have seen, we can use the sine and cosine rules to find the lengths sides and sizes of angles in non-right-angled triangles in two dimensions. We can apply these same techniques to work in three dimensions. This means that we can start to solve more real-world problems.
But working in three dimensions (especially visualising three dimensions on a two-dimensional screen or piece of paper) takes time and practise for most of us. If at first, you find it hard, don’t give up. Working in three dimensions can be learnt. It just needs practise.
Example 3.1
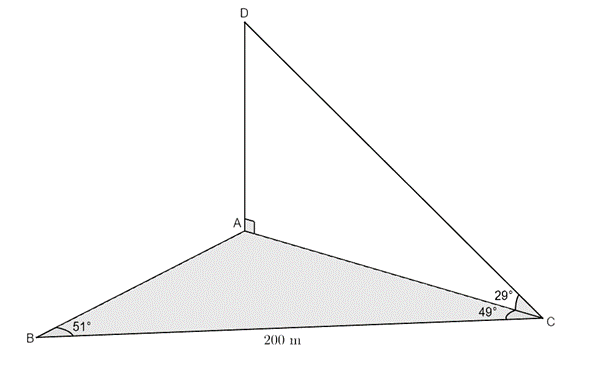
[latex]\scriptsize AD[/latex] is a vertical flagpole and its base, [latex]\scriptsize A[/latex], is in the same horizontal plane as the points [latex]\scriptsize B[/latex] and [latex]\scriptsize C[/latex]. The angle of elevation from point [latex]\scriptsize C[/latex] to the top of the flagpole is [latex]\scriptsize {{29}^\circ}[/latex]. The distance [latex]\scriptsize BC[/latex] is [latex]\scriptsize 200\text{ m}[/latex], [latex]\scriptsize A\hat{B}C={{51}^\circ}[/latex] and [latex]\scriptsize A\hat{C}B={{49}^\circ}[/latex]. Determine the height of the flagpole.
Solution
In this example, a sketch of the situation has been given. Sometimes, you will need to create your own sketch. Notice how [latex]\scriptsize \Delta ABC[/latex] has been shaded. This helps us see that this triangle lies on the ground and is at right angles to the triangle formed by points [latex]\scriptsize A[/latex], [latex]\scriptsize C[/latex] and [latex]\scriptsize D[/latex]. Remember that the flagpole is vertical (meaning it is at right-angles to the ground). The given lengths and angles have been filled in.
We need to calculate the length of [latex]\scriptsize AD[/latex]. We have one angle inside this triangle, and it is a right-angled triangle. Therefore, if we can find the length of [latex]\scriptsize AC[/latex], we can use the tangent ratio to find [latex]\scriptsize AD[/latex]. We choose [latex]\scriptsize AC[/latex] because it is the side shared by both triangles.
We can use the sine rule to calculate [latex]\scriptsize AC[/latex] but, to do so, we first need to calculate the size of [latex]\scriptsize B\hat{A}C[/latex].
[latex]\scriptsize \begin{align*}B\hat{A}C & ={{180}^\circ}-A\hat{B}C-A\hat{C}B\quad (\angle \text{s in }\Delta \text{ suppl)}\\\therefore B\hat{A}C & ={{180}^\circ}-{{51}^\circ}-{{49}^\circ}={{80}^\circ}\\\displaystyle \frac{{AC}}{{\sin {{{51}}^\circ}}} & =\displaystyle \frac{{BC}}{{\sin {{{80}}^\circ}}}\\\therefore AC & =\displaystyle \frac{{200\times \sin {{{51}}^\circ}}}{{\sin {{{80}}^\circ}}}\\\therefore AC & =157.83\end{align*}[/latex]
Remember to keep the full answer for [latex]\scriptsize AC[/latex] in your calculator’s memory. Don’t round off as this will affect the accuracy of your final answer.
Now that we know [latex]\scriptsize AC[/latex], we can find [latex]\scriptsize AD[/latex]:
[latex]\scriptsize \begin{align*}\tan {{29}^\circ} & =\displaystyle \frac{{AD}}{{BC}}\\\therefore AD & =157.83\times \tan {{29}^\circ}\\&=87.48\text{ m}\end{align*}[/latex]
If you are still having difficulty picturing the above situation in your mind, visit this “interactive version of the diagram“. You can click and drag to view the situation from different angles.
Example 3.2
Example adapted from Everything Maths Grade 12 Worked example 16
[latex]\scriptsize D[/latex] is the top of a building of height [latex]\scriptsize h[/latex]. The base of the building is at [latex]\scriptsize A[/latex] and [latex]\scriptsize \Delta ABC[/latex] lies on the ground (a horizontal plane). [latex]\scriptsize BC=b[/latex],[latex]\scriptsize D\hat{B}A=\alpha[/latex], [latex]\scriptsize D\hat{B}C=\beta[/latex] and [latex]\scriptsize D\hat{C}B=\theta[/latex].
Show that [latex]\scriptsize h=\displaystyle \frac{{b\sin \alpha \sin \theta }}{{\sin (\beta +\theta )}}[/latex].
Solution
We are asked to find an expression for [latex]\scriptsize h[/latex]. Because we have been given an angle in [latex]\scriptsize \Delta ABD[/latex], this is the triangle we will focus on. To find [latex]\scriptsize h[/latex], we need to find either[latex]\scriptsize AB[/latex] or [latex]\scriptsize BD[/latex]. [latex]\scriptsize DB[/latex] is a shared side between [latex]\scriptsize \Delta ABD[/latex] and [latex]\scriptsize \Delta BCD[/latex], and [latex]\scriptsize \Delta BCD[/latex] is a good triangle to work in because we have been give information about it. Let’s start by writing an expression for [latex]\scriptsize h[/latex] in [latex]\scriptsize \Delta ABD[/latex].
[latex]\scriptsize \begin{align*}\sin \alpha &=\displaystyle \frac{h}{{BD}}\\\therefore h&=BD\times \sin \alpha \end{align*}[/latex]
Now, let’s find an expression for [latex]\scriptsize BD[/latex] in [latex]\scriptsize \Delta BCD[/latex].
[latex]\scriptsize \begin{align*}\displaystyle \frac{{BD}}{{\sin \theta }} & =\displaystyle \frac{b}{{\sin B\hat{D}C}}\\\therefore BD & =\displaystyle \frac{{b\times \sin \theta }}{{\sin B\hat{D}C}}\end{align*}[/latex]
But we can work out what [latex]\scriptsize B\hat{D}C[/latex] is:
[latex]\scriptsize \begin{align*}B\hat{D}C & ={{180}^\circ}-B\hat{C}D-C\hat{B}D\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\\therefore B\hat{D}C & ={{180}^\circ}-\beta -\theta \end{align*}[/latex]
Therefore:
[latex]\scriptsize \begin{align*}\sin BDC&=\sin ({{180}^\circ}-\beta -\theta )\\&=\sin \left( {{{{180}}^\circ}-(\beta +\theta )} \right)\\&=\sin (\beta +\theta )\end{align*}[/latex]
Therefore:
[latex]\scriptsize BD =\displaystyle \frac{{b\times \sin \theta }}{{\sin (\beta +\theta )}}[/latex]
Now we can replace [latex]\scriptsize BD[/latex] in our original expression with this new expression for [latex]\scriptsize BD[/latex].
[latex]\scriptsize \begin{align*}h&=BD\times \sin \alpha \\&=\displaystyle \frac{{b\times \sin \theta }}{{\sin (\beta +\theta )}}\times \sin \alpha \\&=\displaystyle \frac{{b\sin \alpha \sin \theta }}{{\sin (\beta +\alpha )}}\end{align*}[/latex]
Exercise 3.2
- A cell tower, [latex]\scriptsize AD[/latex], has its base at [latex]\scriptsize A[/latex]. [latex]\scriptsize \Delta ABC[/latex] is a horizontal plane on the ground. The angle of elevation to the top of the tower from [latex]\scriptsize B[/latex] is [latex]\scriptsize \beta[/latex]. A surveyor is standing at [latex]\scriptsize C[/latex] such that he is the same distance, [latex]\scriptsize y[/latex], from [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex]. [latex]\scriptsize A\hat{B}C=\alpha[/latex].
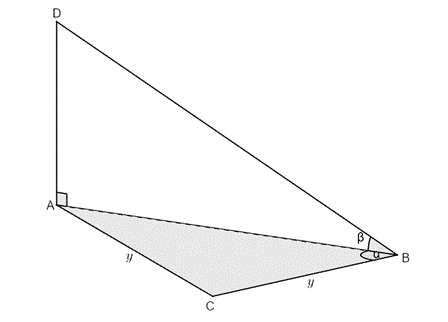
- Find an expression for the height of the tower in terms of [latex]\scriptsize y[/latex], [latex]\scriptsize \alpha[/latex] and [latex]\scriptsize \beta[/latex].
- If it is given that [latex]\scriptsize y=80\text{ m}[/latex], [latex]\scriptsize \alpha ={{39}^\circ}[/latex] and [latex]\scriptsize \beta ={{23}^\circ}[/latex], calculate the height of the tower.
- A building is represented below as [latex]\scriptsize QT[/latex]. [latex]\scriptsize \Delta PQR[/latex] is on the horizontal plane with [latex]\scriptsize Q\hat{P}R={{120}^\circ}[/latex]. [latex]\scriptsize Q\hat{P}T=\beta[/latex] and [latex]\scriptsize P\hat{Q}R=\theta[/latex].

- If [latex]\scriptsize RQ=p[/latex], show that the height of the building, [latex]\scriptsize QT[/latex], is given by [latex]\scriptsize p\tan \beta \left( {\cos \theta -\displaystyle \frac{{\sqrt{3}\sin \theta }}{3}} \right)[/latex].
- If it is further given that [latex]\scriptsize QR=42\text{ m}[/latex], [latex]\scriptsize \theta ={{18}^\circ}[/latex] and [latex]\scriptsize \beta ={{30}^\circ}[/latex], calculate the height of the building to one decimal place.
Question 3 adapted from Everything Maths Grade 12 Exercise 4-6 question 4
- Two ships at sea can see a lighthouse on the shore. The distance from the top of the lighthouse ([latex]\scriptsize H[/latex]) to ship [latex]\scriptsize S[/latex] and to ship [latex]\scriptsize B[/latex] is [latex]\scriptsize 200\text{ m}[/latex]. The angle of elevation from [latex]\scriptsize S[/latex] to [latex]\scriptsize H[/latex] is [latex]\scriptsize \alpha[/latex], [latex]\scriptsize H\hat{B}S=\beta[/latex]and [latex]\scriptsize S\hat{L}B=\theta[/latex].
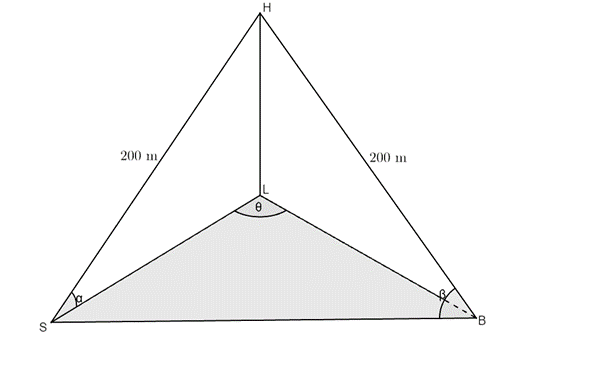
Show that the distance between the two ships is given by [latex]\scriptsize SB=400\cos \beta[/latex].
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- How to use the trigonometric ratios, reduction formulae, compound and double angle formulae, the sine rule, and the cosine rule to solve problems in three dimensions.
Unit 3: Assessment
Suggested time to complete: 35 minutes
Question 1 adapted from NC(V) Level 4 Paper 2 November 2016 question 2.6
- Given below is the side view of a vertical cliff. Points [latex]\scriptsize B[/latex], [latex]\scriptsize C[/latex] and [latex]\scriptsize D[/latex] are on the same horizontal plane. [latex]\scriptsize A[/latex] is a point on the top of the cliff such that [latex]\scriptsize AB\bot BC[/latex]. [latex]\scriptsize BD=30\text{ m}[/latex], [latex]\scriptsize DC=20\text{ m}[/latex], [latex]\scriptsize A\hat{B}C={{90}^\circ}[/latex], [latex]\scriptsize B\hat{D}C={{80}^\circ}[/latex] and [latex]\scriptsize A\hat{C}B={{30}^\circ}[/latex].
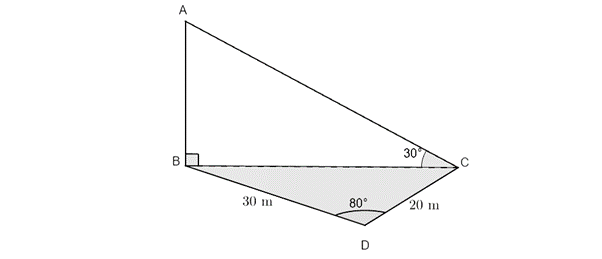
Determine the height of the cliff, [latex]\scriptsize AB[/latex], to one decimal place.
Question 2 adapted from NC(V) Level 4 Paper 2 November 2015 question 2.6
- In the diagram, [latex]\scriptsize AC[/latex] and [latex]\scriptsize BD[/latex] represent the two vertical towers. The points [latex]\scriptsize C[/latex], [latex]\scriptsize D[/latex] and [latex]\scriptsize E[/latex] are on the same horizontal plane. From [latex]\scriptsize E[/latex] the angles of elevation of [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex] are [latex]\scriptsize {{30}^\circ}[/latex] and [latex]\scriptsize {{35}^\circ}[/latex] respectively. [latex]\scriptsize A\hat{E}B={{20}^\circ}[/latex], [latex]\scriptsize CE=5\text{ m}[/latex]and [latex]\scriptsize BD=12\text{ m}[/latex].
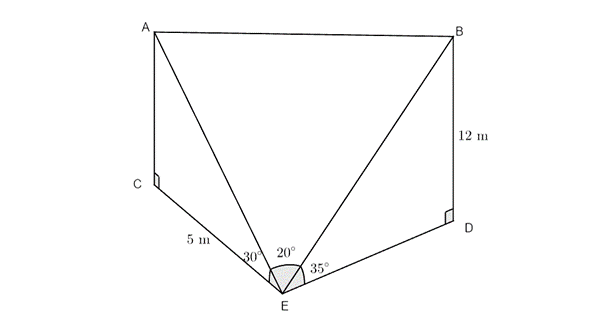
- Calculate the length of [latex]\scriptsize BE[/latex].
- Calculate the length of [latex]\scriptsize AE[/latex].
- Determine the distance, [latex]\scriptsize AB[/latex], between the top of the two towers.
Question 3 adapted from NC(V) Level 4 Paper 2 November 2014 question 2.6
- An eagle, on top of a vertical cliff [latex]\scriptsize AB[/latex], spots two rabbits a distance away. The points [latex]\scriptsize B[/latex], [latex]\scriptsize C[/latex] and [latex]\scriptsize D[/latex] lie in the same horizontal plane. The rabbit at [latex]\scriptsize D[/latex] is [latex]\scriptsize 28.1\text{ m}[/latex] away from the eagle and the angle of elevation from the rabbit at [latex]\scriptsize C[/latex] to the eagle is [latex]\scriptsize {{43}^\circ}[/latex].[latex]\scriptsize BC=20.7\text{ m}[/latex], [latex]\scriptsize B\hat{C}D={{63}^\circ}[/latex] and [latex]\scriptsize C\hat{A}D={{36}^\circ}[/latex].
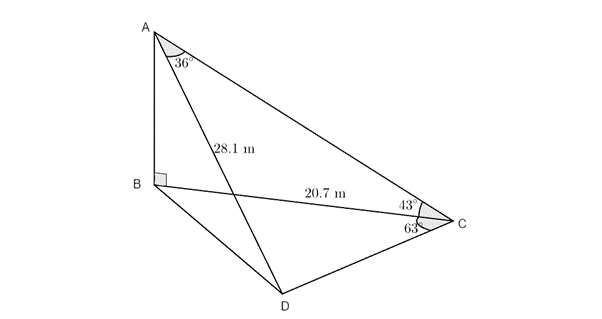
- Calculate the distance between the rabbit at [latex]\scriptsize C[/latex] and the eagle at [latex]\scriptsize A[/latex].
- Calculate the distance between the two rabbits.
The full solutions are at the end of the unit.
Unit 3: Solutions
Exercise 3.1
- .
[latex]\scriptsize \begin{align*}{{q}^{2}} & ={{r}^{2}}+{{p}^{2}}-2rp\cos Q\\\therefore {{q}^{2}} & ={{10}^{2}}+{{15}^{2}}-2\cdot 10\cdot 15\cdot \cos {{36}^\circ}\\\therefore q & =9.07\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin P}}{{15}} & =\displaystyle \frac{{\sin Q}}{{9.07}}\\\therefore \sin P & =\displaystyle \frac{{15\times \sin Q}}{{9.07}}\\\therefore \hat{P} & ={{76.43}^\circ}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}\hat{R} & ={{180}^\circ}-{{36}^\circ}-{{76.43}^\circ}\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\\therefore \hat{R} & ={{67.57}^\circ}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}A\hat{C}B & ={{90}^\circ}\quad \text{(}\angle \text{s in a semi-circle)}\\\therefore C\hat{B}D & ={{90}^\circ}+\theta & \quad \text{(ext }\angle \text{ of }\Delta \text{ = opp int }\angle \text{s)}\\CD & ={{x}^{2}}+{{x}^{2}}-2\cdot x\cdot x\cdot \cos C\hat{B}D\\&=2{{x}^{2}}-2{{x}^{2}}\cos ({{90}^\circ}+\theta )\\&=2{{x}^{2}}-2{{x}^{2}}\left( {-\sin \theta } \right)\\&=2{{x}^{2}}+2{{x}^{2}}\sin \theta \\&=2{{x}^{2}}(1+\sin \theta )\end{align*}[/latex] - .

- .
[latex]\scriptsize \begin{align*}AO & =EO\quad \text{(radii)}\\\therefore O\hat{A}E & =\theta \quad \text{(isos }\Delta \text{)}\\\therefore A\hat{O}C & =2\theta \quad \text{(ext }\angle \text{ of }\Delta \text{ = opp int }\angle \text{s)}\end{align*}[/latex] - In [latex]\scriptsize \Delta ABE[/latex]:
[latex]\scriptsize \cos \theta =\displaystyle \frac{{AE}}{{BE}}[/latex] - In [latex]\scriptsize \Delta ACE[/latex]:
[latex]\scriptsize \sin \theta =\displaystyle \frac{{AC}}{{AE}}[/latex] - In [latex]\scriptsize \Delta ACO[/latex]:
[latex]\scriptsize \sin 2\theta =\displaystyle \frac{{AC}}{{AO}}[/latex] - [latex]\scriptsize \sin 2\theta =\displaystyle \frac{{AC}}{{AO}}[/latex]
But [latex]\scriptsize \sin \theta =\displaystyle \frac{{AC}}{{AE}}[/latex]. Therefore, [latex]\scriptsize AC=AE\sin \theta[/latex]. Therefore, [latex]\scriptsize \sin 2\theta =\displaystyle \frac{{AE\sin \theta }}{{AO}}[/latex].
But [latex]\scriptsize \cos \theta =\displaystyle \frac{{AE}}{{BE}}[/latex]. Therefore, [latex]\scriptsize AE=BE\cos \theta[/latex]. Therefore, [latex]\scriptsize \sin 2\theta =\displaystyle \frac{{BE\cos \theta \sin \theta }}{{AO}}[/latex].
But [latex]\scriptsize BE=2AO[/latex]. Therefore, [latex]\scriptsize \sin 2\theta =\displaystyle \frac{{2AO\cos \theta \sin \theta }}{{AO}}=2\sin \theta \cos \theta[/latex].
- .
- .
- .
[latex]\scriptsize \begin{align*}\sin {{35}^\circ} & =\displaystyle \frac{{AC}}{{CE}}=\displaystyle \frac{7}{{CE}}\\\therefore CE & =\displaystyle \frac{7}{{\sin {{{35}}^\circ}}}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}\sin {{55}^\circ} & =\displaystyle \frac{{BD}}{{DE}}=\displaystyle \frac{{10}}{{DE}}\\\therefore DE & =\displaystyle \frac{{10}}{{\sin {{{55}}^\circ}}}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}C\hat{E}D & ={{180}^\circ}-{{35}^\circ}-{{55}^\circ}={{90}^\circ}\quad \text{(}\angle \text{s on str line suppl)}\\\therefore C{{D}^{2}} & =C{{E}^{2}}+D{{E}^{2}}\quad \text{(Pythagoras)}\\\therefore C{{D}^{2}} & ={{\left( {\displaystyle \frac{7}{{\sin {{{35}}^\circ}}}} \right)}^{2}}+{{\left( {\displaystyle \frac{{10}}{{\sin {{{55}}^\circ}}}} \right)}^{2}}\\\therefore CD & =17.26\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\tan {{35}^\circ} & =\displaystyle \frac{{AC}}{{AE}}=\displaystyle \frac{7}{{AE}}\\\therefore AE & =\displaystyle \frac{7}{{\tan {{{35}}^\circ}}}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}\tan {{55}^\circ} & =\displaystyle \frac{{BD}}{{BE}}=\displaystyle \frac{{10}}{{BE}}\\\therefore BE & =\displaystyle \frac{{10}}{{\tan {{{55}}^\circ}}}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}AB&=AE+BE\\&=\displaystyle \frac{7}{{\tan {{{35}}^\circ}}}+\displaystyle \frac{{10}}{{\tan {{{55}}^\circ}}}\\&=17.00\end{align*}[/latex]
- .
Exercise 3.2
- .
- .
[latex]\scriptsize \begin{align*}\tan \beta & =\displaystyle \frac{{AD}}{{AB}}\\\therefore AD & =AB\times \tan \beta \end{align*}[/latex]
.
In [latex]\scriptsize \Delta ABC[/latex]:
[latex]\scriptsize \begin{align*}B\hat{A}C & =\alpha \quad \text{(isos }\Delta \text{)}\\\therefore A\hat{C}B & ={{180}^\circ}-2\alpha \quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}\displaystyle \frac{{AB}}{{\sin ({{{180}}^\circ}-2\alpha )}} & =\displaystyle \frac{y}{{\sin \alpha }}\\\therefore AB & =\displaystyle \frac{{y\times \sin 2\alpha }}{{\sin \alpha }}\\\therefore AD & =\displaystyle \frac{{y\times \sin 2\alpha }}{{\sin \alpha }}\times \tan \beta \end{align*}[/latex] - [latex]\scriptsize y=80\text{ m}[/latex], [latex]\scriptsize \alpha ={{89}^\circ}[/latex], [latex]\scriptsize \beta ={{23}^\circ}[/latex]:
[latex]\scriptsize \begin{align*}AD & =\displaystyle \frac{{y\times \sin 2\alpha }}{{\sin \alpha }}\times \tan \beta \\&=\displaystyle \frac{{80\sin (2\times {{{39}}^\circ})}}{{\sin {{{39}}^\circ}}}\times \tan {{23}^\circ}\\&=52.78\text{ m}\end{align*}[/latex]
- .
- .
- [latex]\scriptsize p\tan \beta \left( {\cos \theta -\displaystyle \frac{{\sqrt{3}\sin \theta }}{3}} \right)[/latex]
[latex]\scriptsize \begin{align*}\tan \beta & =\displaystyle \frac{{QT}}{{PQ}}\\\therefore QT & =PQ\tan \beta \end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}\hat{R}&={{180}^\circ}-{{120}^\circ}-\theta \quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\&=6{{\text{0}}^\circ}-\theta \end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}\displaystyle \frac{p}{{\sin {{{120}}^\circ}}} & =\displaystyle \frac{{PQ}}{{\sin R}}\\\therefore PQ & =\displaystyle \frac{{p\sin ({{{60}}^\circ}-\theta )}}{{\sin {{{120}}^\circ}}}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}QT & =\displaystyle \frac{{p\sin ({{{60}}^\circ}-\theta )}}{{\sin {{{120}}^\circ}}}\tan \beta \\&=p\tan \beta \left( {\displaystyle \frac{{\sin ({{{60}}^\circ}-\theta )}}{{\sin {{{120}}^\circ}}}} \right)\\&=p\tan \beta \left( {\displaystyle \frac{{\sin {{{60}}^\circ}\cos \theta -\cos {{{60}}^\circ}\sin \theta }}{{\sin {{{60}}^\circ}}}} \right)\\&=p\tan \beta \left( {\displaystyle \frac{{\displaystyle \frac{{\sqrt{3}}}{2}\cos \theta -\displaystyle \frac{1}{2}\sin \theta }}{{\displaystyle \frac{{\sqrt{3}}}{2}}}} \right)\\&=p\tan \beta \left( {\displaystyle \frac{{\displaystyle \frac{{\sqrt{3}\cos \theta -\sin \theta }}{2}}}{{\displaystyle \frac{{\sqrt{3}}}{2}}}} \right)\\&=p\tan \beta \left( {\displaystyle \frac{{\sqrt{3}\cos \theta -\sin \theta }}{2}\times \displaystyle \frac{2}{{\sqrt{3}}}} \right)\\&=p\tan \beta \left( {\displaystyle \frac{{\sqrt{3}\cos \theta -\sin \theta }}{{\sqrt{3}}}} \right)\quad \quad \text{Muliply by }\displaystyle \frac{{\sqrt{3}}}{{\sqrt{3}}}\\&=p\tan \beta \left( {\cos \theta -\displaystyle \frac{{\sqrt{3}\sin \theta }}{3}} \right)\end{align*}[/latex] - [latex]\scriptsize QR=42\text{ m}[/latex], [latex]\scriptsize \theta ={{18}^\circ}[/latex], [latex]\scriptsize \beta ={{30}^\circ}[/latex]:
[latex]\scriptsize \begin{align*}QT&=p\tan \beta \left( {\cos \theta -\displaystyle \frac{{\sqrt{3}\sin \theta }}{3}} \right)\\&=42\tan {{30}^\circ}\left( {\cos {{{18}}^\circ}-\displaystyle \frac{{\sqrt{3}\sin {{{18}}^\circ}}}{3}} \right)\\&=18.7\text{ m}\end{align*}[/latex]
- [latex]\scriptsize p\tan \beta \left( {\cos \theta -\displaystyle \frac{{\sqrt{3}\sin \theta }}{3}} \right)[/latex]
- .
In [latex]\scriptsize \Delta BHS[/latex]:
[latex]\scriptsize \begin{align*}B\hat{S}H & =\beta \quad \text{(isos }\Delta \text{)}\\\therefore B\hat{H}S & ={{180}^\circ}-2\beta \quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\S{{B}^{2}} & ={{200}^{2}}+{{200}^{2}}-2\cdot 200\cdot 200\cdot \cos ({{180}^\circ}-2\beta )\\&=2\times {{200}^{2}}-2\times {{200}^{2}}\times (-\cos 2\beta )\\&=2\times {{200}^{2}}+2\times {{200}^{2}}\times \cos 2\beta \\&=2\times {{200}^{2}}(1+\cos 2\beta )\\&=2\times {{200}^{2}}(1+2{{\cos }^{2}}\beta -1)\\&=2\times {{200}^{2}}(2{{\cos }^{2}}\beta )\\&=4\times {{200}^{2}}{{\cos }^{2}}\beta \\\therefore SB & =2\times 200\times \cos \beta \\&=400\cos \beta \end{align*}[/latex]
Unit 3: Assessment
- .
[latex]\scriptsize \begin{align*}\tan {{30}^\circ} & =\displaystyle \frac{{AB}}{{BC}}\\\therefore AB & =BC\tan {{30}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}B{{C}^{2}} &={{30}^{2}}+{{20}^{2}}-2\cdot 30\cdot 20\cdot \cos {{80}^\circ}\\\therefore BC & =33.04\\\therefore AB &=33.04\tan {{30}^\circ}\\&=19.1\text{ m}\end{align*}[/latex] - .
- .
[latex]\scriptsize \begin{align*}\sin {{35}^\circ} & =\displaystyle \frac{{12}}{{BE}}\\\therefore BE & =\displaystyle \frac{{12}}{{\sin {{{35}}^\circ}}}\\ & =20.92\text{ m}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\cos {{30}^\circ} & =\displaystyle \frac{5}{{AE}}\\\therefore AE & =\displaystyle \frac{5}{{\cos {{{30}}^\circ}}}\\&=5.77\text{ m}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}A{{B}^{2}} & =A{{E}^{2}}+B{{E}^{2}}-2\cdot AE\cdot BE\cdot \cos A\hat{E}B\\&={{5.77}^{2}}+{{20.92}^{2}}-2\cdot 5.77\cdot 20.92\cdot \cos {{20}^\circ}\\\therefore AB & =15.62\text{ m}\end{align*}[/latex]
- .
- .
- .
[latex]\scriptsize \begin{align*}\cos {{43}^\circ} & =\displaystyle \frac{{20.7}}{{AC}}\\\therefore AC & =\displaystyle \frac{{20.7}}{{\cos {{{43}}^\circ}}}\\&=28.30\text{ m}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}C{{D}^{2}} & =A{{D}^{2}}+A{{C}^{2}}-2\cdot AD\cdot AC\cdot \cos C\hat{A}D\\&={{28.1}^{2}}+{{28.3}^{2}}-2\cdot 28.1\cdot 28.3\cdot \cos {{36}^\circ}\\\therefore CD & =17.43\text{ m}\end{align*}[/latex]
- .
Media Attributions
- sinerule © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise 3.1 Q1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise 3.1 Q2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise 3.1 Q3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise 3.1 Q4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example3.1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example3.2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise 3.2 Q1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise 3.2 Q2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise 3.2 Q3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license