Space, shape and measurement: Explore, interpret and justify geometric relationships
Unit 2: Circle geometry theorems
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Apply the following theorems relating to circles:
- Line drawn perpendicular to a chord from the centre of the circle bisects the chord, and its converse (line drawn from the circle centre to the mid-point of chord is perpendicular to the chord).
- Angle at the centre of a circle is twice the size of the angle at the circumference.
- Diameter of a circle subtends a right angle at the circumference, and its converse (if an angle subtended by a chord at a point on the circumference is a right angle, then the chord is a diameter).
- Angles in the same segment of a circle are equal.
What you should know
Before you start this unit, make sure you can:
- Describe the characteristics of the different types of triangles.
- Work with vertically opposite angles and angles on a straight line.
- Work with the alternate, corresponding, and co-interior angles between parallel lines.
Refer to unit 1 of this subject outcome if you need any help with any of these.
Introduction
In the previous unit we learnt about and used the properties of angles on straight lines and in triangles. We noted that studying geometry in general, and circle geometry in particular, is an excellent way to help us develop and hone our logic, reasoning and argumentation skills. Being able to reason logically and express our reasons and arguments clearly and concisely is an important and valuable life skill.
In that unit, we used the basic ‘facts’ of angles on straight lines and in triangles to construct arguments to prove relationships between angles that were not immediately obvious. We used .
These basic ‘facts’ (such as that angles on a straight line add up to [latex]\scriptsize {{180}^\circ}[/latex]) are called axioms – statements that are assumed to be true for the purposes of building further arguments. Axioms are sometimes called self-evident truths or postulates. The whole of mathematics is based on several crucial axioms that, if ever proven untrue, would undo entire branches of mathematics.
One such axiom is called the reflexive axiom and states that a number is equal to itself. In other words, [latex]\scriptsize a=a[/latex]. This seems completely obvious (a self-evident truth or an axiom), but it underpins all of mathematics. Another, that we rely upon in many geometry arguments, is the transitive axiom (if [latex]\scriptsize a=b[/latex] and [latex]\scriptsize b=c[/latex] then [latex]\scriptsize a=c[/latex]).
Did you know?
There are six fundamental axioms for algebra. You can read clear and simple explanations of these axioms of algebra at this link.
Many of these are mirrored in the seven axioms that Euclid stated for geometry. Visit an Introduction to Euclidean Geometry for more details.
Some basics
Sometimes, we use the fundamental axioms to build reusable arguments called theorems. These are non-self-evident statements of truth that we prove once and then keep using to build other arguments without having to prove them each time. Theorems can also be built upon by other theorems. If ever the underlying axioms (or theorems) were proven untrue, the theorem could no longer be taken to be true. This is why mathematicians spend so much time carefully and meticulously proving that every statement they make is true.
Did you know?
There is a famous theorem called Fermat’s last theorem. It says that there are no solutions to the equation [latex]\scriptsize {{a}^{n}}+{{b}^{n}}={{c}^{n}}[/latex] for any value of [latex]\scriptsize n[/latex] greater than [latex]\scriptsize 2[/latex]. You should recognise the case when [latex]\scriptsize n=2[/latex] as the theorem of Pythagoras.
This theorem was assumed to be true for hundreds of years without any formal or official proof. Whole areas of mathematics were built on this theorem that were at risk! Finally, in 1993, a mathematician called Andrew Wiles presented the first proof. It took him almost six years to develop and three days to present!
Unfortunately, there was an error in his proof which took him another year to correct. Finally, in 1995, the final theorem was published in the form of two papers.

Watch the excellent video called “Fermat’s Last Theorem” if you want to learn more.
There are a number of theorems that relate to circles. We will learn about four of them in this unit. In order to understand what they mean, we need to make sure that we know what the different parts of a circle are called. Study figure 2 to learn about the parts of a circle if you don’t know them already.
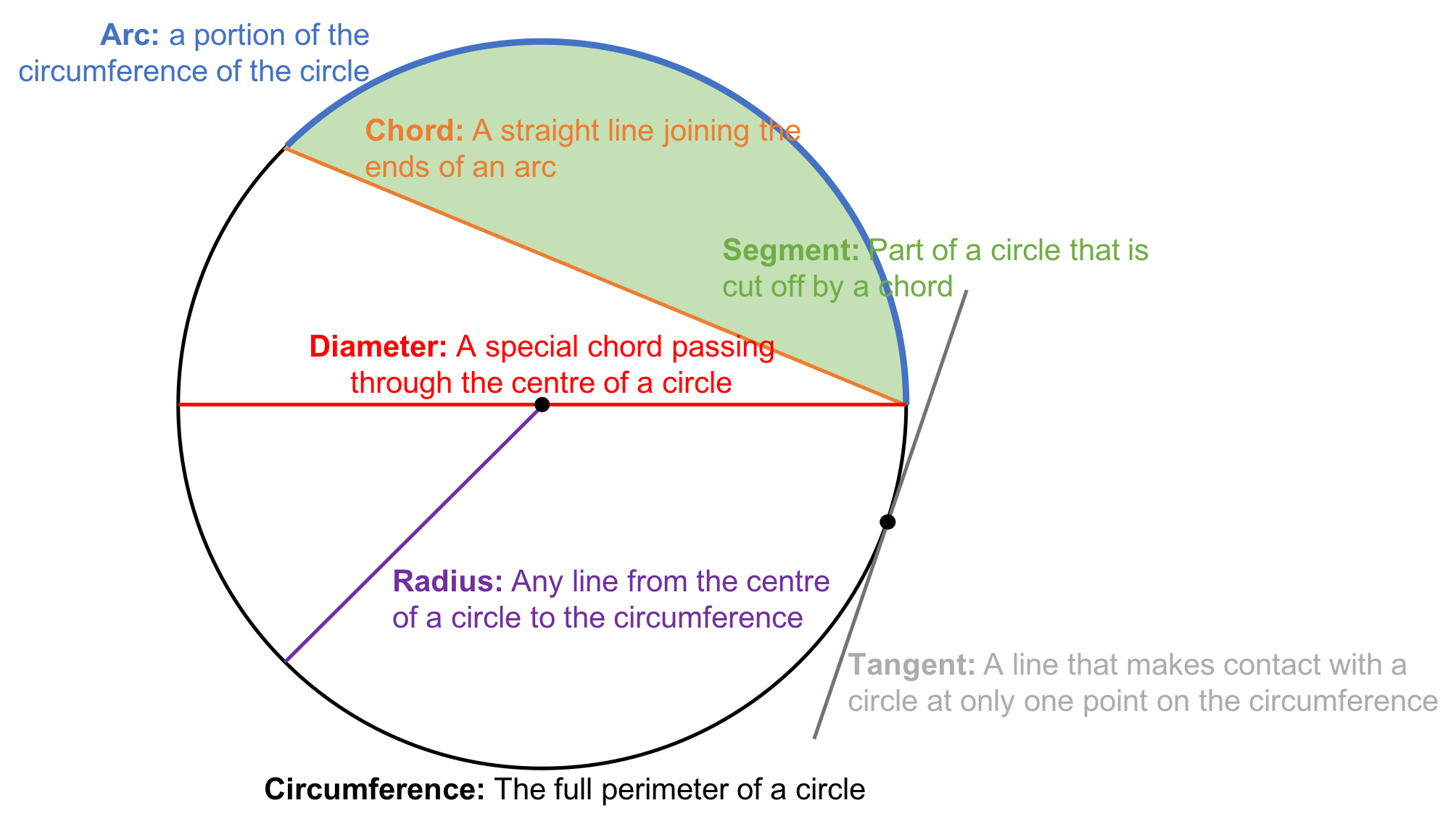
Circle theorems
You do not need to be able to prove any of the circle theorems yourself. You can simply assume that they are true. The following sections explain the theorems that you need to be able to state and use. Note that they are numbered only for reference purposes. These theorems do not have official numbers.
Theorem 1
This circle theorem deals with chords.
Theorem 1: Perpendicular line from circle centre bisects chord
If a line is drawn from the centre of a circle perpendicular (at right angles) to a chord, then it bisects the chord.
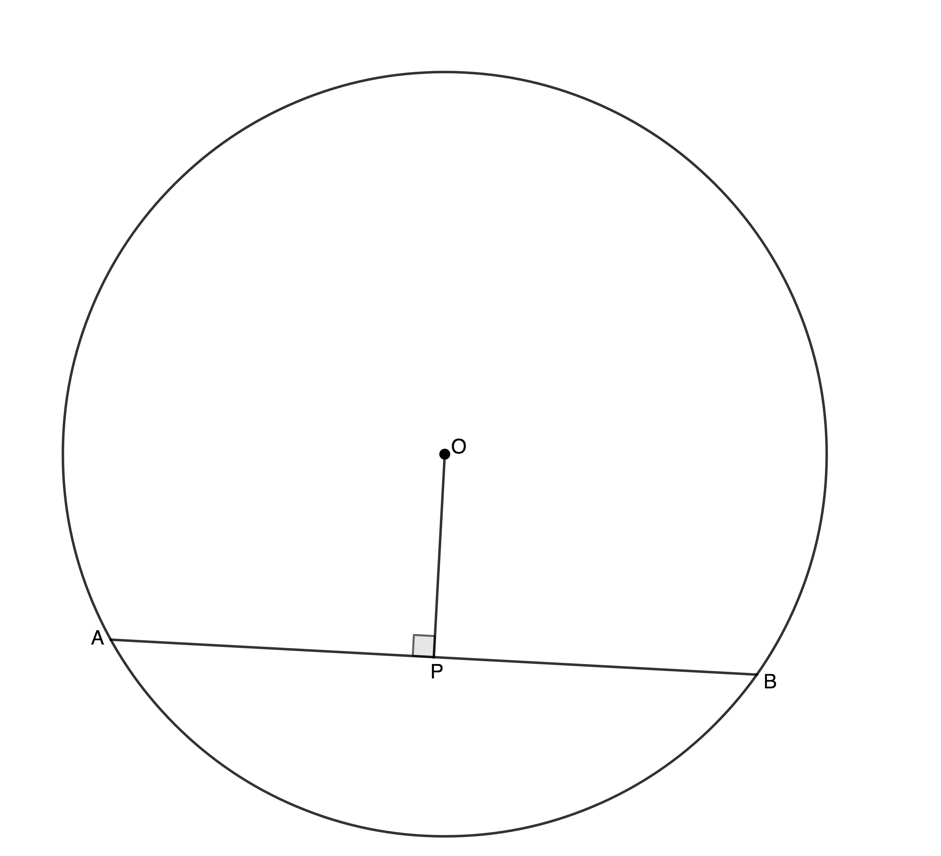
If [latex]\scriptsize OP[/latex] is perpendicular to [latex]\scriptsize AB[/latex], then [latex]\scriptsize OP[/latex] bisects [latex]\scriptsize AB[/latex] (i.e. [latex]\scriptsize \displaystyle AP=BP[/latex] ).
Reason: [latex]\scriptsize \bot[/latex] (or perp) from centre bisects chord
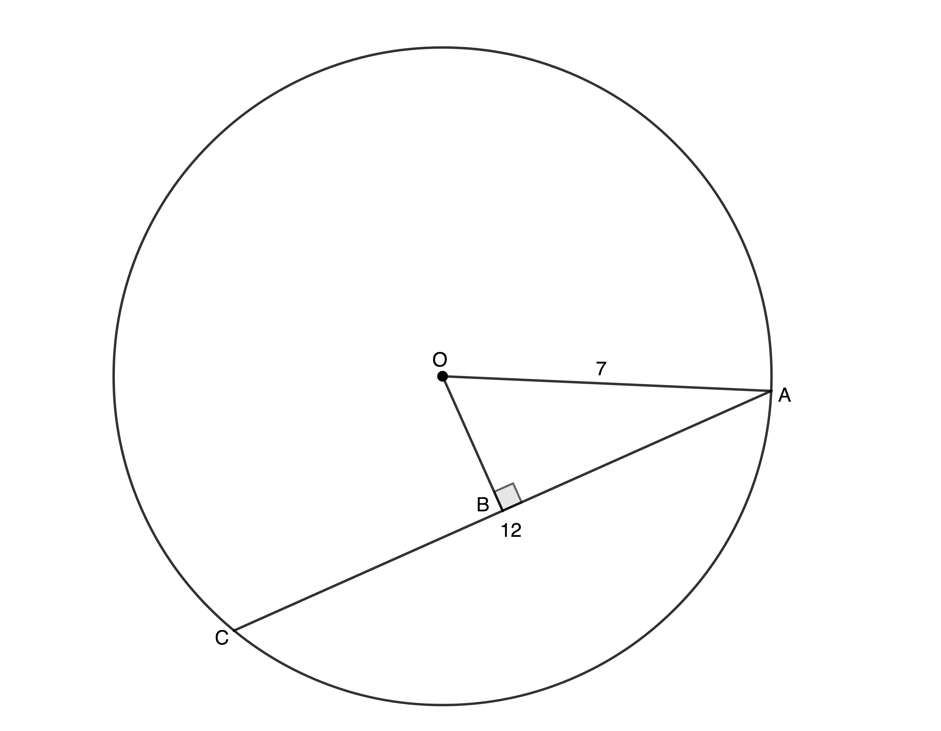
Example 2.1
Given [latex]\scriptsize OB\bot AC[/latex], [latex]\scriptsize OA=7\text{ units}[/latex] and [latex]\scriptsize AC=12\text{ units}[/latex], determine the length of [latex]\scriptsize OB[/latex].
Solution
We need to recognise that the line from the centre meets the chord [latex]\scriptsize AB[/latex] at right angles and bisects the chord or cuts it in half.
[latex]\scriptsize AB=\displaystyle \frac{1}{2}AC=6\text{ units}\quad (\bot \text{ from centre bisects chord)}[/latex]
In [latex]\scriptsize \Delta ABO[/latex]:
[latex]\scriptsize \displaystyle \begin{align*}\hat{B}=90{}^\circ \text{ Given}\\O{{A}^{2}} & =O{{B}^{2}}+A{{B}^{2}}\quad \text{(Pythagoras)}\\\therefore O{{B}^{2}} & =O{{A}^{2}}-A{{B}^{2}}\\\therefore O{{B}^{2}} & ={{7}^{2}}-{{6}^{2}}\\&=49-36\\&=13\\\therefore OB & =\sqrt{{13}}\end{align*}[/latex]
A converse of a theorem can be thought of as the reverse of a theorem. If a theorem states that ‘if [latex]\scriptsize A[/latex] is true then [latex]\scriptsize B[/latex] is true’ then the converse of the theorem says that ‘if [latex]\scriptsize B[/latex] is true then[latex]\scriptsize A[/latex] is true’. Not all theorems have converses that are also true, but many do.
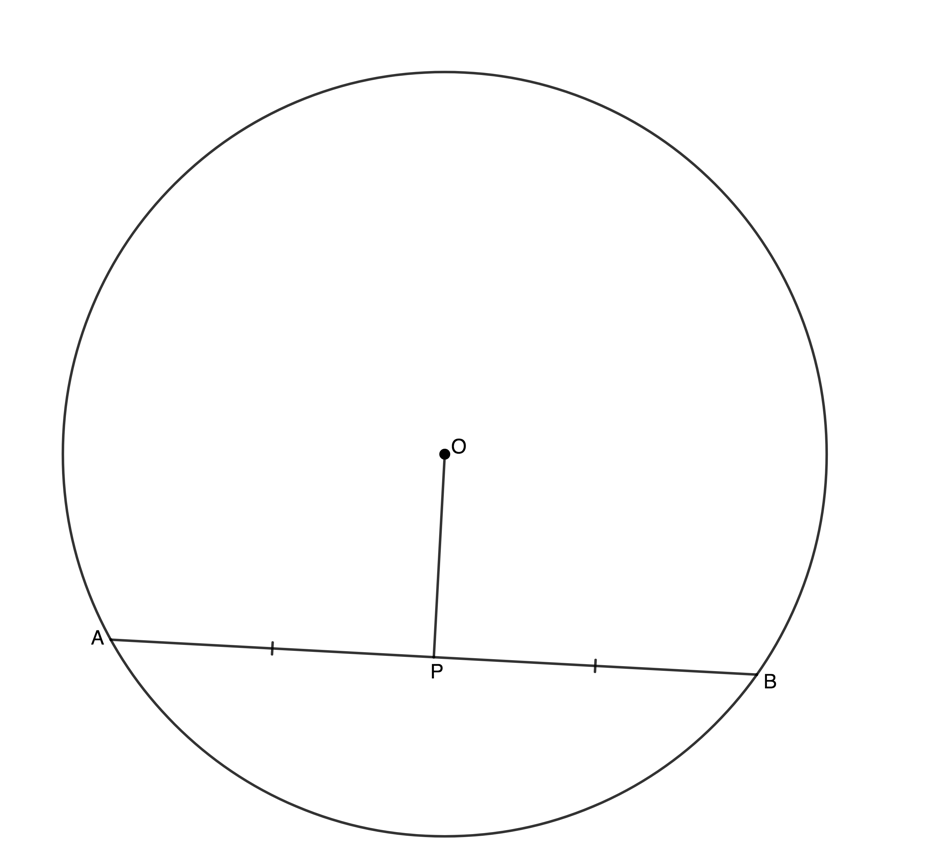
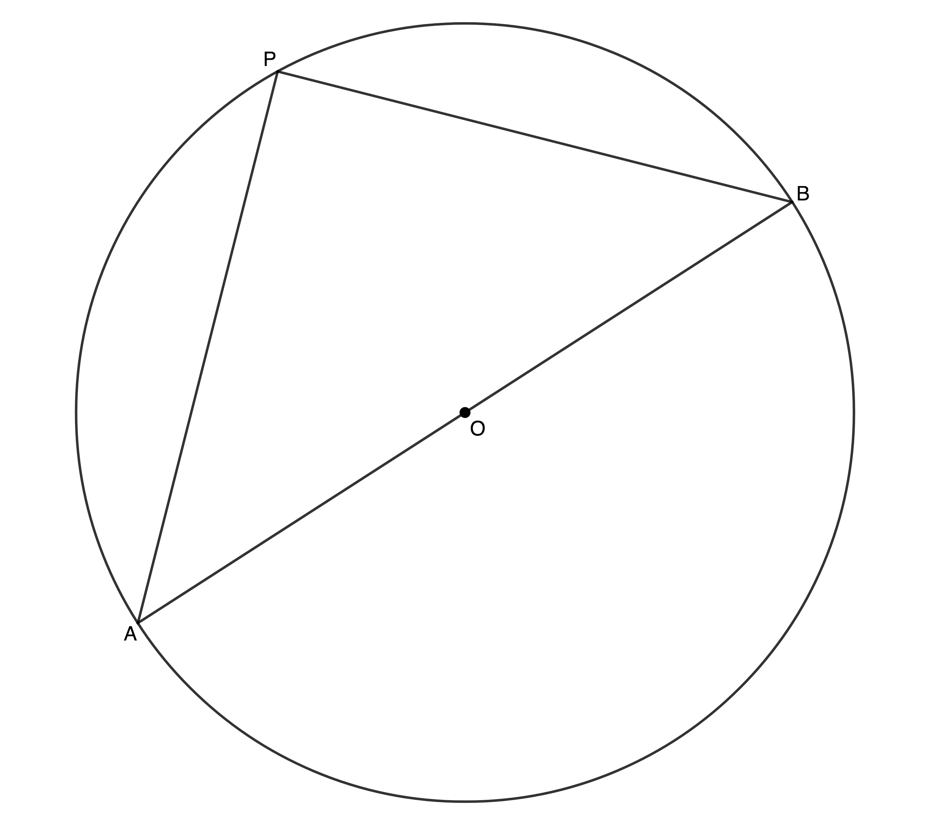
Converse to theorem 1: Line from circle centre to mid-point of chord is perpendicular to the chord
If a line is drawn from the centre of a circle to the mid-point of a chord, then the line is perpendicular to the chord.
If [latex]\scriptsize OP[/latex] bisects [latex]\scriptsize AB[/latex] (i.e. [latex]\scriptsize AP=BP[/latex]), then [latex]\scriptsize OP[/latex] is perpendicular to [latex]\scriptsize AB[/latex].
Reason: Line from centre to mid-point [latex]\scriptsize \bot[/latex] (or perp)
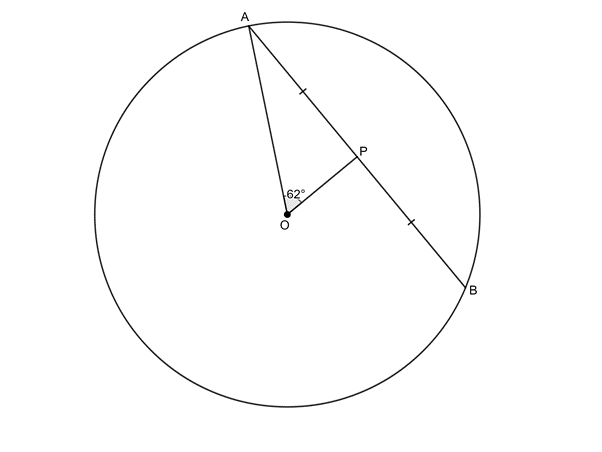
Example 2.2
Given [latex]\scriptsize AP=BP[/latex] and [latex]\scriptsize P\hat{O}A={{62}^\circ}[/latex], determine the [latex]\scriptsize O\hat{A}P[/latex].
Solution
We need to recognise that we are dealing with the converse of theorem 1. If a line from the centre bisects a chord, then it meets the chord at right-angles.
[latex]\scriptsize O\hat{P}A={{90}^\circ}\quad (\text{Line from centre to mid-point }\bot )[/latex]
In [latex]\scriptsize \Delta AOP[/latex]:
[latex]\scriptsize \displaystyle \begin{align*}O\hat{A}P & ={{180}^\circ}-{{90}^\circ}-{{62}^\circ}\quad \left( {\angle \text{s in }\!\!\Delta\!\!\text{ suppl}} \right)\\\therefore O\hat{A}P&={{28}^\circ}\end{align*}[/latex]
Theorems 2 and 3
Let’s now look at two more circle theorems.
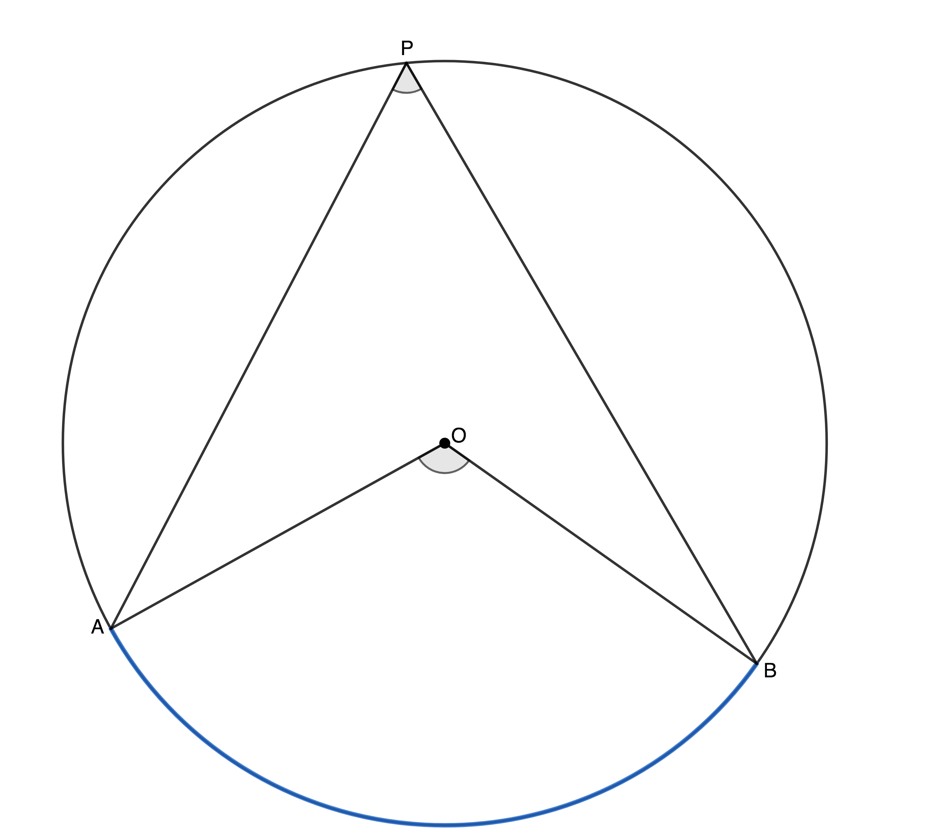
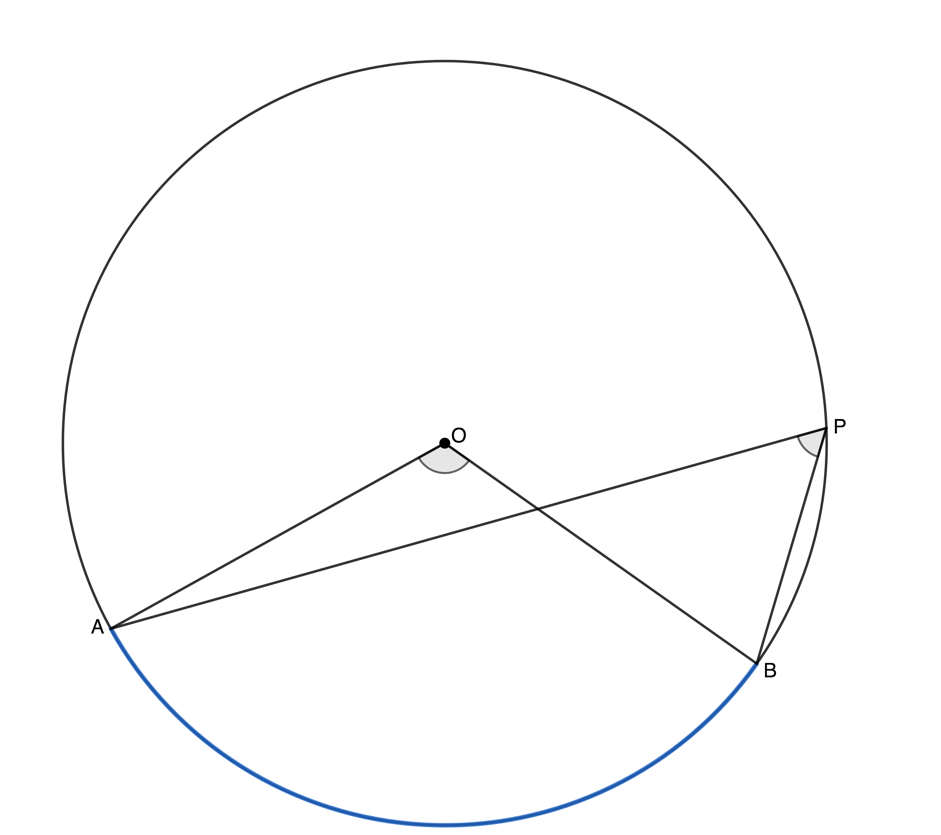
Theorem 2: Angle at the centre of a circle is twice the size of the angle at the circumference
If an arc subtends an angle at the centre of a circle and at the circumference, then the angle at the centre is twice the size of the angle at the circumference.
Note: We say an arc subtends an angle when the lines creating that angle start at either end of the arc. We can also say that the angle is subtended by the relevant chord. Three different possibilities are illustrated.
If arc [latex]\scriptsize AB[/latex] (or chord [latex]\scriptsize AB[/latex]) subtends an angle at the centre and an angle at the circumference, then the angle at the centre ([latex]\scriptsize A\hat{O}B[/latex]) is twice the size of the angle at the circumference ([latex]\scriptsize A\hat{P}B[/latex]).
Reason: [latex]\scriptsize \angle[/latex] at centre = [latex]\scriptsize 2\angle[/latex] at circumference.
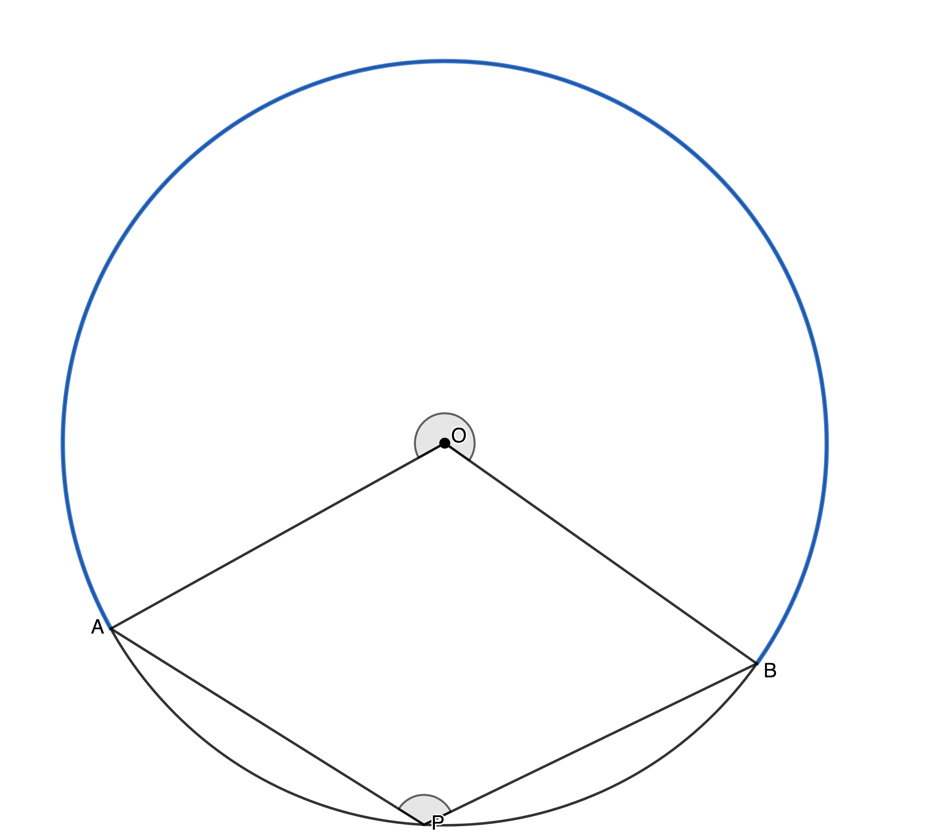
Visit this activity to play with an interactive circle to explore theorem 2 in more detail.
Move point [latex]\scriptsize C[/latex] to change the size of the arc (or chord) and hence the angles created and then drag point A around the circumference of the circle. What happens if you make the arc a diameter?
You should have seen that if the arc subtending an angle is a diameter then the angle at the centre will be [latex]\scriptsize {{180}^\circ}[/latex]. This means that the angle at the circumference will be [latex]\scriptsize {{90}^\circ}[/latex]. Therefore, a diameter will subtend an angle of [latex]\scriptsize {{90}^\circ}[/latex] at the circumference. This is theorem 3.
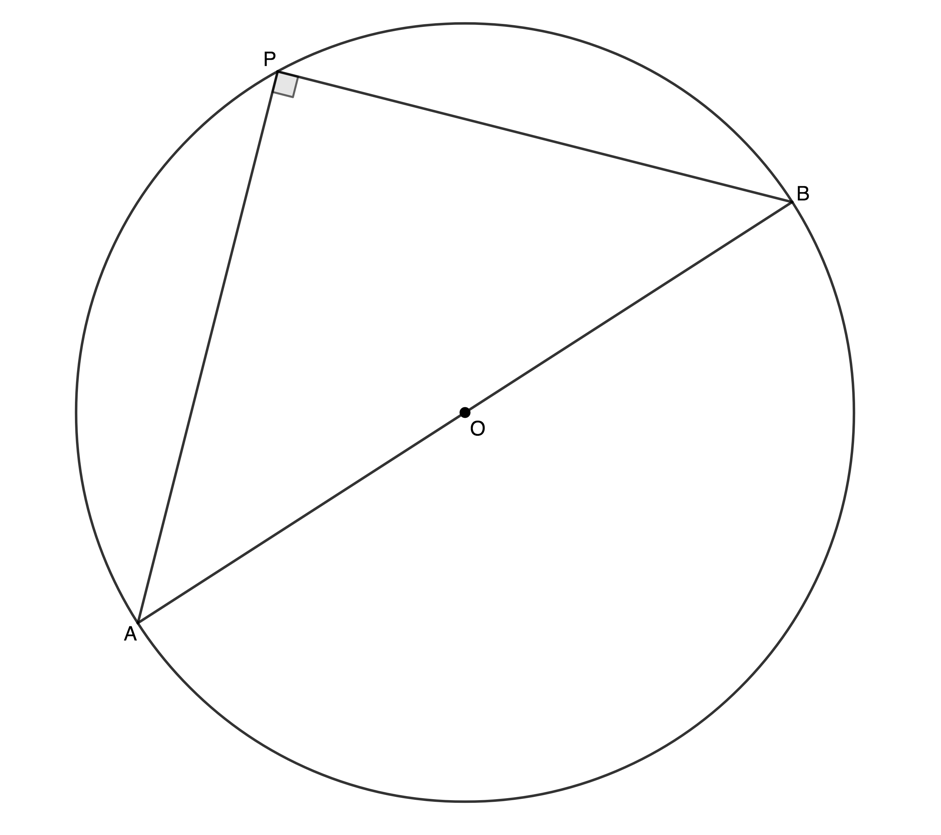
Theorem 3: Diameter of a circle subtends a right angle at the circumference
If a diameter subtends an angle at the circumference, then this angle is a right angle.
If [latex]\scriptsize AB[/latex] is a diameter, then the angle subtended at the circumference ([latex]\scriptsize A\hat{P}B[/latex]) is a right angle.
Reason: Angles in a semi-circle
Converse to theorem 3: If a chord subtends a right angle at the circumference then the chord is a diameter
If an angle subtended by a chord at a point on the circumference is a right angle, then the chord is a diameter.
If [latex]\scriptsize AB[/latex] subtends a right-angle at the circumference, then [latex]\scriptsize AB[/latex] is a diameter.
Reason: Chord subtends right-angle
Example 2.3
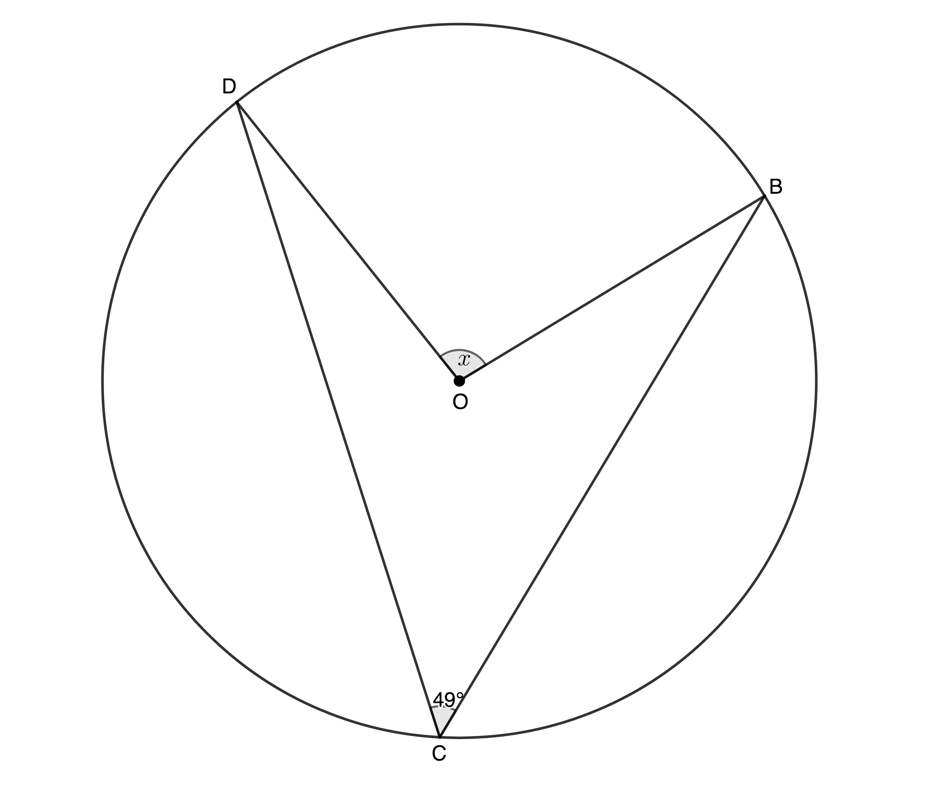
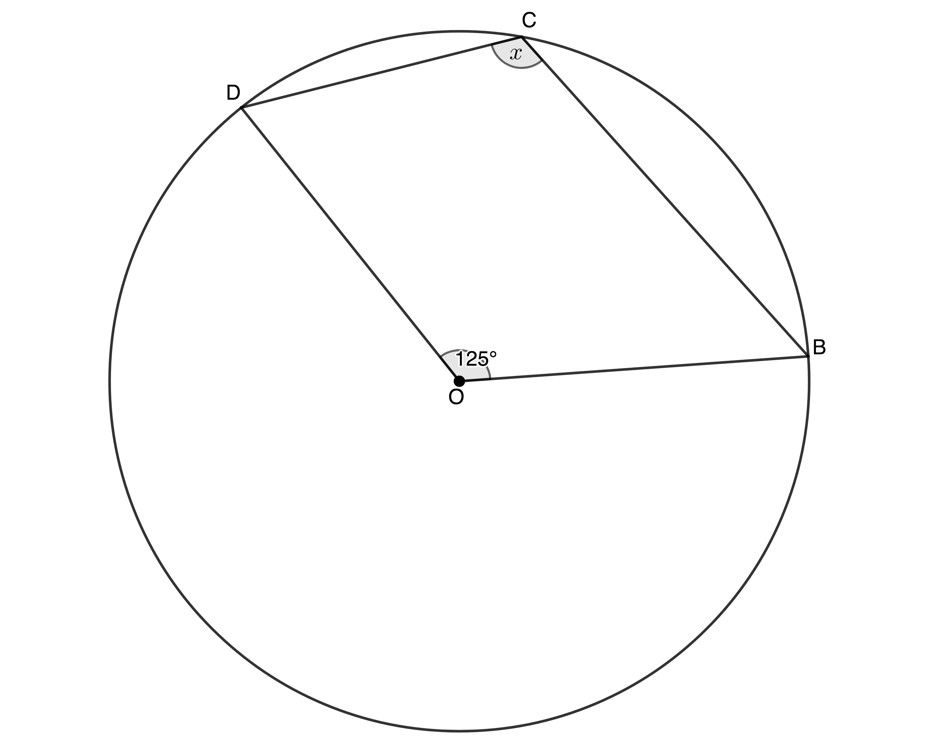
Given [latex]\scriptsize O[/latex] the centre of the circle, determine the value of [latex]\scriptsize x[/latex] in each case.
Solution
- Arc [latex]\scriptsize \displaystyle DB[/latex] (or chord [latex]\scriptsize \displaystyle DB[/latex]) subtends an angle of [latex]\scriptsize {{49}^\circ}[/latex] at the circumference and angle [latex]\scriptsize D\hat{O}B[/latex] at the centre.
.
[latex]\scriptsize D\hat{O}B=x=2\times {{49}^\circ}={{98}^\circ}\quad (\angle \text{ at centre 2}\angle \text{ at circumference)}[/latex] - We need to be careful in this case because the angle at the circumference and the given angle at the centre are not on the same side of the chord [latex]\scriptsize \displaystyle DB[/latex]. Instead, we need to consider the larger arc [latex]\scriptsize \displaystyle DB[/latex] as indicated below. Therefore, the angle at the centre is actually [latex]\scriptsize {{235}^\circ}[/latex].
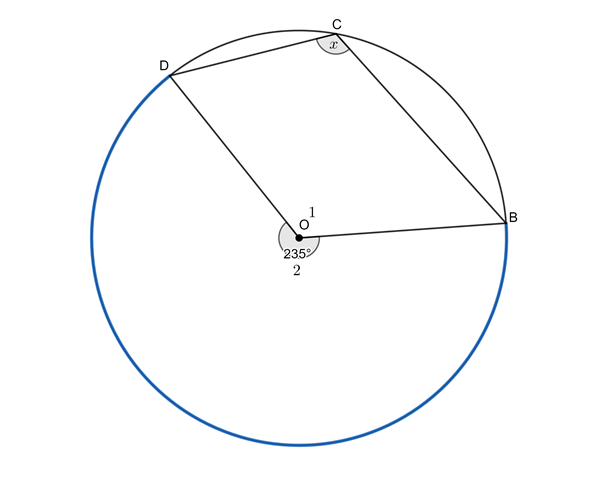
[latex]\scriptsize \begin{align*}{{{\hat{O}}}_{2}}&={{360}^\circ}-{{{\hat{O}}}_{1}}\quad (\text{angles around a point = 36}{{\text{0}}^\circ})\\&={{360}^\circ}-{{125}^\circ}\\&={{235}^\circ}\end{align*}[/latex]
[latex]\scriptsize \displaystyle B\hat{C}D=x={{\displaystyle \frac{{235}}{2}}^\circ}={{117.5}^\circ}\quad \left( {\angle \text{at centre =2}\angle \text{ at circumference}} \right)[/latex]
Example 2.4
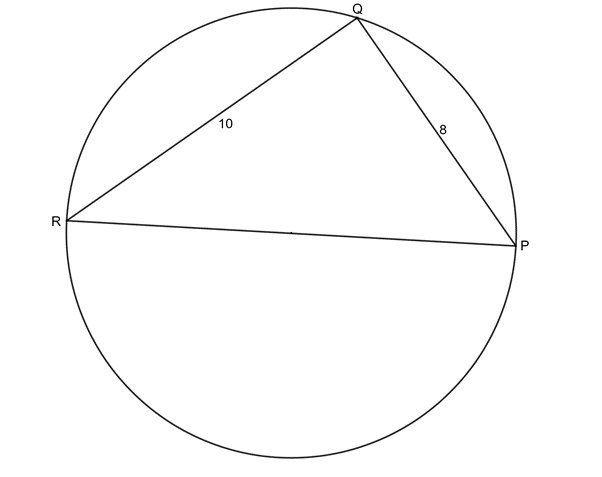
Given [latex]\scriptsize PR[/latex] a diameter of the circle [latex]\scriptsize PQR[/latex], [latex]\scriptsize PQ=8\text{ units}[/latex]and [latex]\scriptsize QR=10\text{ units}[/latex], determine the radius of the circle [latex]\scriptsize PQR[/latex].
Solution
We are told that [latex]\scriptsize PR[/latex] is a diameter. Therefore, it subtends an angle of [latex]\scriptsize {{90}^\circ}[/latex] at the circumference. Therefore, [latex]\scriptsize \Delta PQR[/latex] is a right-angled triangle and we can use Pythagoras to determine the length of the diameter and, hence, the length of the radius.
[latex]\scriptsize PR[/latex] is a diameter (given)
Therefore [latex]\scriptsize P\hat{Q}R={{90}^\circ}\quad \text{(}\angle \text{s in a semi-circle)}[/latex]
In [latex]\scriptsize \Delta PQR[/latex]:
[latex]\scriptsize \begin{align*}P{{R}^{2}} & =P{{Q}^{2}}+Q{{R}^{2}}\quad (\text{Pythagoras})\\&={{8}^{2}}+{{10}^{2}}\\&=164\\\therefore PR & =2\sqrt{{41}}\text{ units}\end{align*}[/latex]
A radius is equal to half the diameter. Therefore, the radius is [latex]\scriptsize \sqrt{{41}}\text{ units}[/latex].
Theorem 4
This next theorem deals with segments of a circle.
Theorem 4: Angles in the same segment of a circle are equal
If the angles subtended by a chord of the circle are on the same side of the chord, then the angles are equal.
If [latex]\scriptsize AB[/latex] subtends angles [latex]\scriptsize \displaystyle A\hat{P}B[/latex] and [latex]\scriptsize A\hat{Q}B[/latex] at the circumference and [latex]\scriptsize \displaystyle A\hat{P}B[/latex] and are both on the same side of the chord [latex]\scriptsize AB[/latex], then [latex]\scriptsize \displaystyle A\hat{P}B=A\hat{Q}B[/latex].
Reason: [latex]\scriptsize \angle[/latex]s in same seg
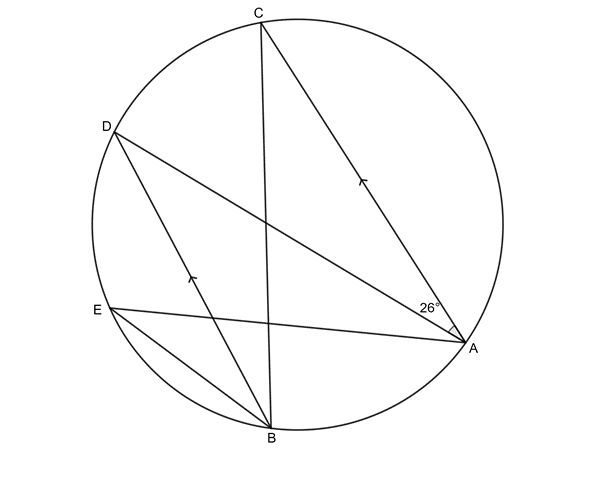
Example 2.5
Given [latex]\scriptsize C\hat{A}D={{26}^\circ}[/latex], determine the sizes of angles [latex]\scriptsize \hat{C}[/latex], [latex]\scriptsize \hat{D}[/latex] and [latex]\scriptsize \hat{E}[/latex].
Solution
[latex]\scriptsize \hat{D}={{26}^\circ}\quad \text{(alt }\angle \text{s =;AC}\parallel \text{BD)}[/latex]
[latex]\scriptsize \hat{C}=\hat{D}={{26}^\circ}\quad \text{(}\angle \text{s in same seg)}[/latex]
[latex]\scriptsize \hat{E}=\hat{D}={{26}^\circ}\quad \text{(}\angle \text{s in same seg)}[/latex]
Exercise 2.1
- Find the values of the unknown angles in each case. Note that where O appears, it is the centre of the circle.
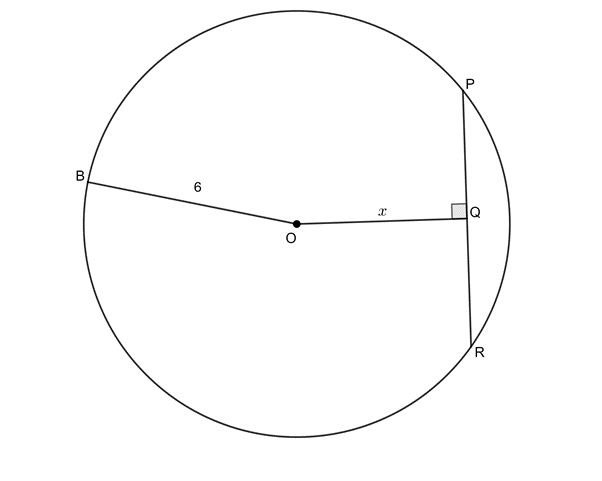
- In the circle with centre [latex]\scriptsize O[/latex], the radius is [latex]\scriptsize \text{6 units}[/latex] [latex]\scriptsize OQ\bot PR[/latex] and [latex]\scriptsize PR=8\text{ units}[/latex]. Determine [latex]\scriptsize x[/latex].
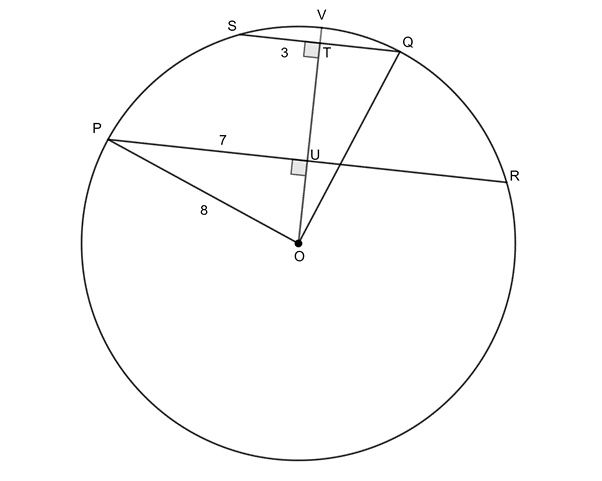
- In the circle with centre [latex]\scriptsize O[/latex], [latex]\scriptsize OT\bot SQ[/latex], [latex]\scriptsize OT\bot PR[/latex], [latex]\scriptsize OP=8\text{ units}[/latex], [latex]\scriptsize ST=3\text{ units}[/latex] and [latex]\scriptsize PU=7\text{ units}[/latex]. Determine [latex]\scriptsize TU[/latex].
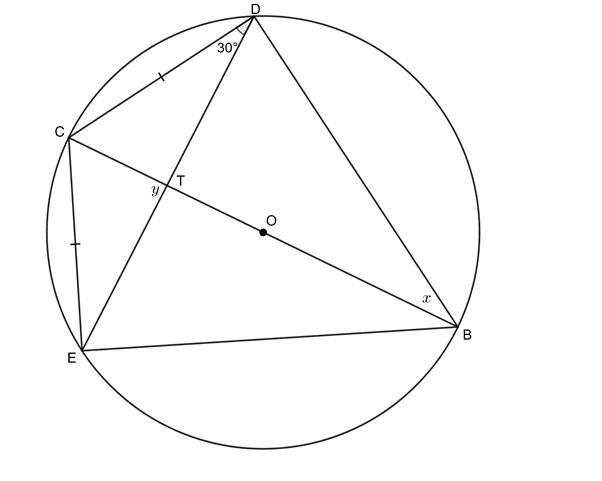
- Given circle with centre [latex]\scriptsize O[/latex], [latex]\scriptsize CD=CE[/latex] and [latex]\scriptsize C\hat{D}T={{30}^\circ}[/latex]. Determine [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex]. Does [latex]\scriptsize OC[/latex] bisect [latex]\scriptsize DE[/latex]?
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- A line drawn perpendicular to a chord from the centre of the circle bisects the chord.
- A line drawn from the circle centre to the mid-point of chord is perpendicular to the chord.
- The angle subtended by an arc or chord at the centre of a circle is twice the size of the angle subtended at the circumference.
- The diameter of a circle subtends a right angle at the circumference.
- If an angle subtended by a chord at a point on the circumference is a right angle, then the chord is a diameter.
- Angles subtended by the same arc or chord in the same segment of a circle (on the same side of the chord) are equal.
Unit 2: Assessment
Suggested time to complete: 40 minutes
Question 1 adapted from NC(V) Mathematics Level 4 Paper 2 November 2011 question 1.2
- AB is a diameter of the circle with centre [latex]\scriptsize E[/latex]. [latex]\scriptsize C\hat{D}E={{50}^\circ}[/latex] and [latex]\scriptsize AB\parallel DC[/latex].
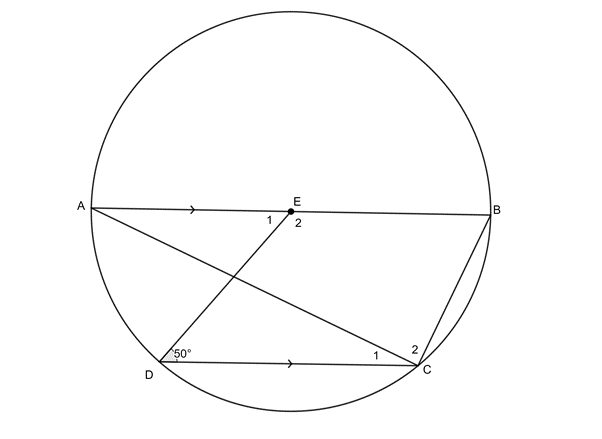
Determine, with reasons, the values of [latex]\scriptsize {{\hat{E}}_{1}}[/latex], [latex]\scriptsize {{\hat{C}}_{1}}[/latex] and [latex]\scriptsize \hat{B}[/latex].
Question 2 adapted from NC(V) Mathematics Level 4 Paper 2 November 2013 question 1.2
- In the diagram below, [latex]\scriptsize O[/latex] is the centre of the circle with diameters [latex]\scriptsize AC[/latex] and [latex]\scriptsize BD[/latex]. [latex]\scriptsize AB\parallel DC[/latex] and [latex]\scriptsize AC[/latex] meets [latex]\scriptsize BD[/latex] at [latex]\scriptsize O[/latex]. [latex]\scriptsize P[/latex] is any point on the minor arc [latex]\scriptsize BC[/latex]. [latex]\scriptsize PB[/latex] and [latex]\scriptsize PC[/latex] are joined.
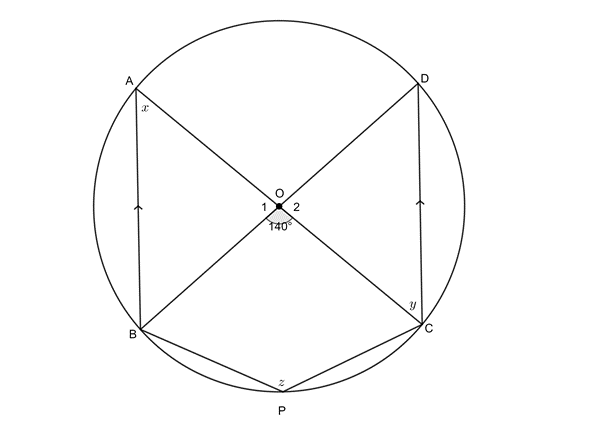
Calculate, with reasons, the values of [latex]\scriptsize x[/latex], [latex]\scriptsize y[/latex] and [latex]\scriptsize z[/latex].
Question 3 adapted from NC(V) Mathematics Level 4 Paper 2 November 2014 question 1.3
- In the figure given below, [latex]\scriptsize O[/latex] is the centre of the circle with diameter [latex]\scriptsize BD[/latex]. [latex]\scriptsize A\hat{O}B={{60}^\circ}[/latex] and [latex]\scriptsize B\hat{D}C={{22}^\circ}[/latex]with [latex]\scriptsize A[/latex] and [latex]\scriptsize C[/latex] any two points on the circle on either side of [latex]\scriptsize BD[/latex].
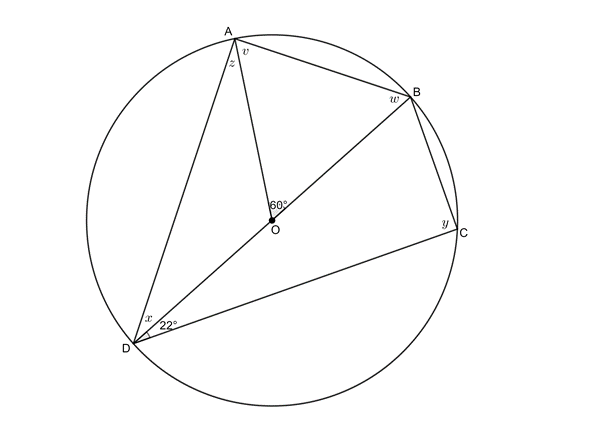
Determine, with reasons, the values of [latex]\scriptsize v[/latex], [latex]\scriptsize w[/latex], [latex]\scriptsize x[/latex], [latex]\scriptsize y[/latex] and [latex]\scriptsize z[/latex].
Question 4 adapted from NC(V) Mathematics Level 4 Paper 2 November 2015 question 1.3
- In the figure below [latex]\scriptsize O[/latex] is the centre of the circle, [latex]\scriptsize AOD[/latex] is a diameter and [latex]\scriptsize AE\parallel CD[/latex], with [latex]\scriptsize E[/latex], [latex]\scriptsize C[/latex] and [latex]\scriptsize B[/latex] on the circumference of the circle. Also, [latex]\scriptsize \hat{A}={{50}^\circ}[/latex].
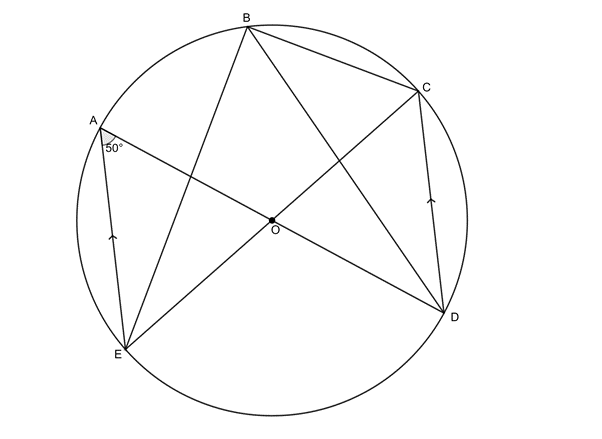
- Why is [latex]\scriptsize A\hat{D}C={{50}^\circ}[/latex]?
- Determine the size of [latex]\scriptsize C\hat{B}D[/latex].
- Prove that [latex]\scriptsize EOC[/latex] is a straight line.
The full solutions are at the end of the unit.
Unit 2: Solutions
Exercise 2.1
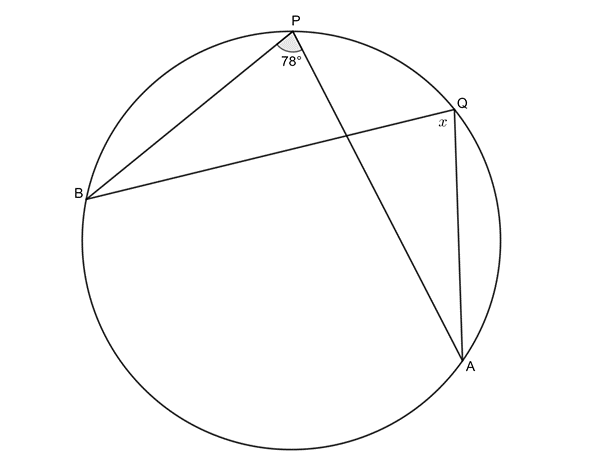
- .
- [latex]\scriptsize x={{78}^\circ}\quad \text{(}\angle \text{s in same seg)}[/latex]
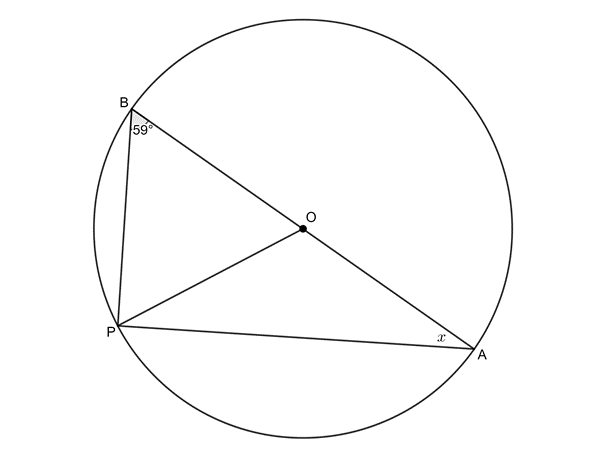
- [latex]\scriptsize AB[/latex] is a diameter (straight line passing through the centre)
Therefore [latex]\scriptsize A\hat{P}B={{90}^\circ}\quad (\angle \text{s in semi-circle)}[/latex]
[latex]\scriptsize \begin{align*}x&={{180}^\circ}-{{90}^\circ}-{{59}^\circ}\quad \text{(}\angle \text{s in a }\Delta \text{)}\\&={{31}^\circ}\end{align*}[/latex] - .
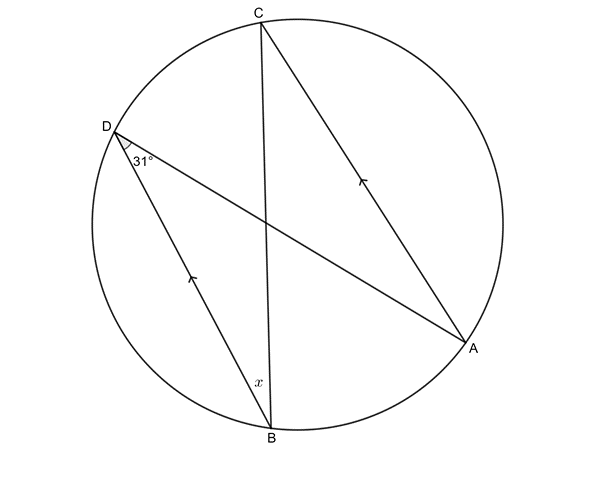
[latex]\scriptsize \begin{align*}C\hat{A}D & ={{31}^\circ}\quad \text{(alt }\angle \text{s =; }AC\parallel BD\text{)}\\x=C\hat{A}D & ={{31}^\circ}\quad \text{(}\angle \text{s in same seg)}\end{align*}[/latex] - .
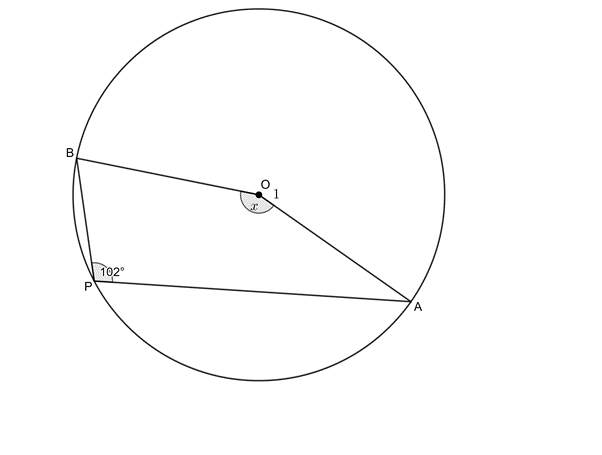
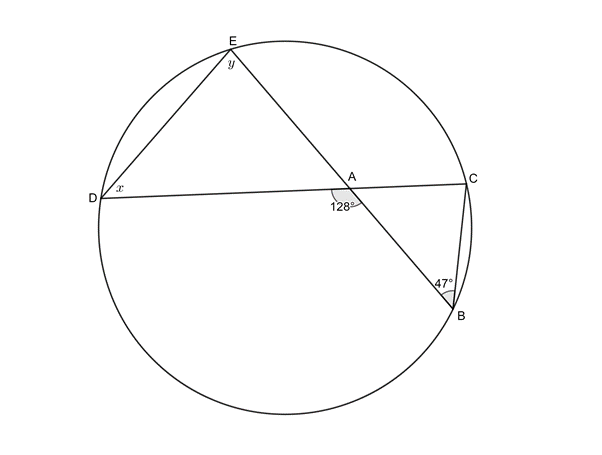
[latex]\scriptsize \begin{align*}{{{\hat{O}}}_{1}} & ={{204}^\circ}\quad \text{(}\angle \text{ at centre =2}\angle \text{ at circumference)}\\\therefore x & ={{360}^\circ}-{{204}^\circ}\quad \text{(}\angle \text{ }\!\!'\!\!\text{ s round a point)}\\ & ={{156}^\circ}\end{align*}[/latex] - [latex]\scriptsize x={{47}^\circ}\quad \text{(}\angle \text{s in same seg)}[/latex]
[latex]\scriptsize \begin{align*}D\hat{A}E & ={{180}^\circ}-{{128}^\circ}\quad \text{(}\angle \text{s on str line suppl)}\\ & ={{52}^\circ}\\\therefore y & ={{180}^\circ}-{{52}^\circ}-{{47}^\circ}\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\ &=8{{\text{1}}^\circ}\end{align*}[/latex]
- [latex]\scriptsize OP=OB=6\text{ units}\quad \text{(both radii)}[/latex]
[latex]\scriptsize \begin{align*}PR & =8\text{ units}\quad \text{(given)}\\\therefore PQ & =4\text{ units}\quad \text{(}\bot \text{ from centre bisects chord)}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{x}^{2}} & =O{{P}^{2}}-P{{Q}^{2}}\quad \text{(Pythagoras)}\\\therefore {{x}^{2}} & ={{6}^{2}}-{{4}^{2}}\\&=36-16\\&=20\\\therefore x & =2\sqrt{5}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}O{{U}^{2}} & =O{{P}^{2}}-P{{U}^{2}}\quad \text{(Pythagoras)}\\\therefore O{{U}^{2}} & ={{8}^{2}}-{{7}^{2}}\\=64-49\\=15\\\therefore OU & =\sqrt{{15}}\end{align*}[/latex]
[latex]\scriptsize OP=OQ=8\text{ units}\quad \text{(both radii)}[/latex]
[latex]\scriptsize QT=ST=3\text{ units}\quad \text{(}\bot \text{ from centre bisects chord)}[/latex]
[latex]\scriptsize \begin{align*}O{{T}^{2}} & =O{{Q}^{2}}-Q{{T}^{2}}\quad \text{(Pythagoras)}\\\therefore O{{T}^{2}} & ={{8}^{2}}-{{3}^{2}}\\=64-9\\=55\\\therefore OT & =\sqrt{{55}}\end{align*}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}TU=OT-OU\\=\sqrt{{55}}-\sqrt{{15}}\end{align*}[/latex] - .
[latex]\scriptsize C\hat{E}D={{30}^\circ}\quad \text{(isos }\Delta \text{)}[/latex]
[latex]\scriptsize x=C\hat{E}D={{30}^\circ}\quad \text{(}\angle \text{s in same seg)}[/latex]
[latex]\scriptsize \begin{align*}B\hat{D}C & ={{90}^\circ}\quad \text{(}CB\text{ passes through centre O; }\angle \text{s in semi-circle)}\\\therefore E\hat{D}B & ={{60}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}E\hat{C}T & ={{60}^\circ}\quad \text{(}\angle \text{s in same seg)}\\\therefore y & ={{180}^\circ}-{{30}^\circ}-{{60}^\circ}\quad \text{(}\angle \text{s in }\Delta \text{ suppl)}\\ & ={{90}^\circ}\end{align*}[/latex]
Therefore [latex]\scriptsize OC[/latex] bisects [latex]\scriptsize DE[/latex] ([latex]\scriptsize \bot[/latex] from centre bisects chord).
Unit 2: Assessment
- .
[latex]\scriptsize {{\hat{E}}_{1}}={{50}^\circ}\quad \text{(alt }\angle \text{s =; }AB\parallel CD\text{)}[/latex]
[latex]\scriptsize \displaystyle {{\hat{C}}_{1}}=\displaystyle \frac{1}{2}{{\hat{E}}_{1}}={{25}^\circ}\quad \text{(}\angle \text{ at centre =2}\angle \text{ at circumference)}[/latex][latex]\scriptsize \begin{align*}{{{\hat{C}}}_{2}} & ={{90}^\circ}\quad \text{(}\angle \text{s in semi-circle)}\\\hat{B}+{{{\hat{C}}}_{1}}+{{{\hat{C}}}_{2}} & ={{180}^\circ}\quad \text{(co-int }\angle \text{s suppl; }AB\parallel CD\text{)}\\\therefore \hat{B} & ={{180}^\circ}-{{90}^\circ}-{{25}^\circ}={{65}^\circ}\end{align*}[/latex] - .
[latex]\scriptsize x={{70}^\circ}\quad \text{(}\angle \text{ at centre =2}\angle \text{ at circumference)}[/latex]
[latex]\scriptsize y=x={{70}^\circ}\quad \text{(alt }\angle \text{ }\!\!'\!\!\text{ s =; }AB\parallel CD\text{)}[/latex]
[latex]\scriptsize \begin{align*}{{{\hat{O}}}_{1}}+{{{\hat{O}}}_{2}}+A\hat{O}D & ={{360}^\circ}-{{140}^\circ}={{220}^\circ}\quad \text{(}\angle \text{s around a point)}\\\therefore z & ={{110}^\circ}\quad \text{(}\angle \text{ at centre =2}\angle \text{ at circumference)}\end{align*}[/latex] - .
In [latex]\scriptsize \Delta ABO[/latex]:
[latex]\scriptsize \begin{align*}OA & =OB\quad \text{(both radii)}\\\therefore v & =w\quad \text{(isosc }\Delta \text{)}\\\therefore 2v & ={{180}^\circ}-{{60}^\circ}={{120}^\circ}\quad \text{(}\angle \text{s in a }\Delta \text{ suppl)}\\\therefore v & ={{60}^\circ}\\\therefore w & ={{60}^\circ}\end{align*}[/latex]
[latex]\scriptsize x={{30}^\circ}\quad \text{(}\angle \text{ at centre= 2}\angle \text{ at circumference)}[/latex]
[latex]\scriptsize y={{90}^\circ}\quad \text{(}\angle \text{s in semi-circle)}[/latex]
[latex]\scriptsize \begin{align*}z+v & ={{90}^\circ}\quad \text{(}\angle \text{s in semi-circle)}\\\therefore z & ={{30}^\circ}\end{align*}[/latex] - .
- [latex]\scriptsize A\hat{D}C={{50}^\circ}\quad \text{(alt }\angle \text{s =; }AE\parallel CD\text{)}[/latex]
- In [latex]\scriptsize \Delta AOE[/latex]:
[latex]\scriptsize \begin{align*}OA & =OE\quad \text{(both radii)}\\\therefore \hat{A}=A\hat{E}O\quad \text{(isosc }\Delta \text{)}\\\therefore A\hat{O}E & ={{180}^\circ}-{{50}^\circ}-{{50}^\circ}={{80}^\circ}\quad \text{(}\angle \text{s in a }\Delta \text{ suppl)}\\A\hat{O}E=C\hat{O}D={{80}^\circ}\text{ (vert opp }\angle \text{s})\\\therefore C\hat{B}D & ={{40}^\circ}\quad \text{(}\angle \text{ at centre =2}\angle \text{ at circumference)}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}E\hat{B}D & ={{50}^\circ}\quad \text{(}\angle \text{s in same seg)}\\E\hat{B}C & =E\hat{B}D+C\hat{B}D\\ & ={{40}^\circ}+{{50}^\circ}\\={{90}^\circ}\\\therefore EOC\text{ } & \text{is a diameter (chord subtend right-angle)}\end{align*}[/latex]
Therefore [latex]\scriptsize EOC[/latex] is a straight line.
Media Attributions
- figure1 © Klaus Barner is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure2 © DHET is licensed under a CC BY (Attribution) license
- theorem1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example2.1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- theorem1converse © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example2.2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- theorem2a © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- theorem2b © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- theorem2c © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- theorem3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- theorem3converse © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example2.3 Q1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example2.3 Q2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example2.3 A2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example2.4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- theorem4 © Geogebra
- example2.5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise2.1 Q1a © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise2.1 Q1b © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise2.1 Q1c © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise2.1 Q1d © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise2.1 Q1e © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise2.1 Q2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise2.1 Q3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise2.1 Q4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
Deductive reasoning (also called deductive logic), is the process of reasoning from one or more statements or premises to reach a logical conclusion. If the premises are true, then the conclusion MUST be true. Deductive reasoning is an example of top-down logic.