Functions and algebra: Investigate and use instantaneous rate of change of a variable when interpreting models both in mathematical and real life situations
Unit 1: Use first principles to find the derivative
Natashia Bearam-Edmunds
Unit outcomes
By the end of this unit you will be able to:
- Define the derivative using limits.
- Calculate the derivative from first principles.
What you should know
Before you start this unit, make sure you can:
- Find limits of a function as shown in level 3 subject outcome 2.5 unit 1. You may also watch this video to revise limits, “Introduction to limits”.
..
- Find the average gradient of a function. To revise this refer to level 3 subject outcome 2.5 unit 2.
Introduction
Cheetahs are the fastest land animal, reaching speeds of up to 113 km/h. But, cheetahs do not run at their top speed at every instant. So, how do we calculate their speed at any given instant?
Before calculus was invented there was no way to calculate instantaneous speed. Calculus makes the study of the smallest rates of change possible. Key to the concept of calculus is finding the limits of functions.
The type of limit we use to find the slope of the tangent line to a function at a point has many applications. It allows us to get the most or the best, out of any deal. This limit occurs so frequently that we give it a special name; the derivative. The process of finding a derivative is called differentiation.
Limits revised
In level 3 subject outcome 2.5 unit 1, we saw that when a function approaches the same y-value from the left and from the right, the limit exists. The limit of a function is shown with the following notation: [latex]\scriptsize \underset{{x\to a}}{\mathop{{\lim }}}\,f(x)=L[/latex].
Example 1.1
Find [latex]\scriptsize \underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{2}}-9}}{{x-3}}[/latex].
Solution
If you substitute [latex]\scriptsize x=3[/latex] directly into the expression you will get [latex]\scriptsize \displaystyle \frac{0}{0}[/latex], which is undefined. To find the limit we must first simplify the expression.
[latex]\scriptsize \begin{align*}\underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{2}}-9}}{{x-3}}&=\underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{\cancel{{(x-3)}}(x+3)}}{{\cancel{{(x-3)}}}}\\&=\underset{{x\to 3}}{\mathop{{\lim }}}\,(x+3)\\&=6\end{align*}[/latex]
Example 1.2
Find: [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{2}}+x}}{{3x-2}}[/latex].
Solution
If the degree of the numerator is greater than the degree of the denominator, then the limit will either be positive infinity or negative infinity. We have to look at the signs of the terms with the largest exponents in both the numerator and denominator.
[latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{2}}+x}}{{3x-2}}=+\infty[/latex]
This is because both [latex]\scriptsize {{x}^{2}}[/latex] in the numerator and [latex]\scriptsize 3x[/latex] in the denominator are positive.
While [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{4{{x}^{2}}-5{{x}^{3}}}}{{3x-2}}=-\infty[/latex] because [latex]\scriptsize \displaystyle \frac{{-5}}{3}[/latex] is negative.
Revise limits by completing the following exercise.
Exercise 1.1
Calculate:
- [latex]\scriptsize \underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{h}^{2}}+4h}}{h}[/latex]
- [latex]\scriptsize \underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{{(2+h)}}^{2}}-4}}{h}[/latex]
- [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{2}}+1}}{{{{x}^{2}}+1}}[/latex]
The full solutions are at the end of the unit.
Average rate of change
Remember that the gradient of a line passing through the points [latex]\scriptsize \text{A}({{x}_{\text{A}}};{{y}_{\text{A}}})[/latex] and [latex]\scriptsize \text{B}({{x}_{\text{B}}};{{y}_{\text{B}}})[/latex] is found using the formula:
[latex]\scriptsize \displaystyle \begin{align*}m&=\displaystyle \frac{{{{y}_{\text{B}}}-{{y}_{\text{A}}}}}{{{{x}_{\text{B}}}-{{x}_{\text{A}}}}}\\&=\displaystyle \frac{{\Delta y}}{{\Delta x}}\end{align*}[/latex].
The gradient of a linear function is constant.
With curved graphs the gradient changes at every point on the curve so we need to work with the average gradient. Remember that the average gradient between two points is equal to the gradient of a straight line, called a secant, drawn between the two points.
To find the average gradient between any two points on a curve we calculate the gradient of the secant line that passes through both points.
Note
The average rate of change tells us whether the new change produced an increase, decrease or no change and how fast the change occurred, on average.
The average rate of change or average gradient of a function between [latex]\scriptsize \text{A}({{x}_{\text{A}}};{{y}_{\text{A}}})[/latex] and [latex]\scriptsize \text{B}({{x}_{\text{B}}};{{y}_{\text{B}}})[/latex] is given by:
[latex]\scriptsize \displaystyle \begin{align*}\displaystyle \frac{{\Delta y}}{{\Delta x}}&=\displaystyle \frac{{{{y}_{\text{B}}}-{{y}_{\text{A}}}}}{{{{x}_{\text{B}}}-{{x}_{\text{A}}}}}\\&=\displaystyle \frac{{f({{x}_{\text{B}}})-f({{x}_{\text{A}}})}}{{{{x}_{\text{B}}}-{{x}_{\text{A}}}}}\end{align*}[/latex]
Remember that [latex]\scriptsize \displaystyle f({{x}_{B}})={{y}_{B}}[/latex]

If we let the change in [latex]\scriptsize x[/latex] values equal [latex]\scriptsize h[/latex] then [latex]\scriptsize \displaystyle {{x}_{B}}-{{x}_{A}}=h[/latex]. Therefore, [latex]\scriptsize \displaystyle {{x}_{B}}=h+{{x}_{A}}[/latex].
So, the average rate of change of a function between [latex]\scriptsize \text{A}({{x}_{\text{A}}};{{y}_{\text{A}}})[/latex] and [latex]\scriptsize \text{B}({{x}_{\text{B}}};{{y}_{\text{B}}})[/latex] can be rewritten as [latex]\scriptsize \displaystyle \displaystyle \frac{{f({{x}_{A}}+h)-f({{x}_{\text{A}}})}}{h}[/latex].
Example 1.3
Use the formula [latex]\scriptsize \displaystyle \displaystyle \frac{{f({{x}_{1}}+h)-f({{x}_{1}})}}{h}[/latex] to determine the average gradient of the curve [latex]\scriptsize \displaystyle f\left( x \right)=x\left( {x\text{ }+\text{ }3} \right)[/latex] between [latex]\scriptsize \displaystyle x=5[/latex] and [latex]\scriptsize \displaystyle x=3[/latex].
Solution
Method 1:
[latex]\scriptsize f(x)={{x}^{2}}+3x[/latex]
[latex]\scriptsize \displaystyle \begin{align*}f({{x}_{1}}+h)&=f(5+h)\\&={{(5+h)}^{2}}+3(5+h)\\&=25+10h+{{h}^{2}}+15+3h\\&={{h}^{2}}+13h+40\end{align*}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}f(5)&={{5}^{2}}+3(5)\\&=40\end{align*}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}\displaystyle \frac{{f({{x}_{1}}+h)-f({{x}_{1}})}}{h}&=\displaystyle \frac{{{{h}^{2}}+13h+40-40}}{h}\\&=\displaystyle \frac{{{{h}^{2}}+13h}}{h}\\&=\displaystyle \frac{{h(h+13)}}{h}\\&=h+13\end{align*}[/latex]
Find [latex]\scriptsize h[/latex]
[latex]\scriptsize \begin{align*}h&=x{}_{B}-{{x}_{A}}\\&=3-5\\&=-2\end{align*}[/latex]
Substitute the value of [latex]\scriptsize h=-2[/latex] into the average gradient expression and the average gradient is [latex]\scriptsize \displaystyle -2+13[/latex], which is equal to [latex]\scriptsize 11[/latex].
Method 2:
We can rewrite the average gradient formula as: [latex]\scriptsize \displaystyle \frac{{f(a+h)-f(a)}}{{(a+h)-a}}=\displaystyle \frac{{f(a+h)-f(a)}}{h}[/latex]where [latex]\scriptsize a[/latex] is the x-value we start from, and [latex]\scriptsize h={{x}_{B}}-{{x}_{A}}[/latex] as in method 1.
Find an expression for the average gradient.
[latex]\scriptsize \displaystyle \begin{align*}\displaystyle \frac{\begin{align*}f(x)={{x}^{2}}+3x\\f(a+h)-f(a)\end{align*}}{h}&=\displaystyle \frac{{{{{(a+h)}}^{2}}+3(a+h)-({{a}^{2}}+3a)}}{h}\\&=\displaystyle \frac{{{{a}^{2}}+2ah+{{h}^{2}}+3a+3h-{{a}^{2}}-3a}}{h}\\&=\displaystyle \frac{{2ah+{{h}^{2}}+3h}}{h}\\&=\displaystyle \frac{{\cancel{h}(2a+h+3)}}{{\cancel{h}}}\\&=2a+h+3\end{align*}[/latex]
Note: we start at [latex]\scriptsize \displaystyle {{x}_{1}}=a=5[/latex] therefore substitute [latex]\scriptsize a=5[/latex].
[latex]\scriptsize \begin{align*}h&=x{}_{B}-{{x}_{A}}\\&=3-5\\&=-2\end{align*}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}\text{Average gradient}&=2a+h+3\\&=2(5)-2+3\\&=11\end{align*}[/latex]
The average rate of change gives the average or net change of a function over an interval and is useful, for example, in the study of climate change, population growth and economics.
Exercise 1.2
Use the formula [latex]\scriptsize \displaystyle \displaystyle \frac{{f(a+h)-f(a)}}{h}[/latex] to find the average gradient of [latex]\scriptsize f(x)={{x}^{2}}-x-2[/latex] between the points with the following x-coordinates:
- [latex]\scriptsize \displaystyle {{x}_{1}}=2[/latex] and [latex]\scriptsize \displaystyle {{x}_{2}}=5[/latex]
- [latex]\scriptsize \displaystyle {{x}_{1}}=5[/latex] and [latex]\scriptsize \displaystyle {{x}_{2}}=2[/latex]
- [latex]\scriptsize \displaystyle {{x}_{1}}=-2[/latex] and [latex]\scriptsize \displaystyle {{x}_{2}}=-1[/latex]
The full solutions are at the end of the unit.
Note
This ‘Applet’ gives an interactive demonstration of gradient between two points.
Gradient at a point
The way a function changes at a single point has even more uses than the average rate of change between two points. The way a function changes at a particular instant is known as the instantaneous rate of change at the point. Limits are used to calculate the gradient of a function at a specific point on a curve.
Make sure you have revised limits of a function (level 3 subject outcome 2.5 unit 1) where the limit is defined. We saw in level 3 subject outcome 2.5 unit 2 that the gradient of any curve at any point is the same as the gradient of the tangent at that point.
Let’s revise what you learnt in level 3 subject outcome 2.5 unit 2 activity 2.1.
Imagine that there is a point B that moves closer and closer to a fixed point [latex]\scriptsize \text{A}(1,6)[/latex] as shown in figure 2.
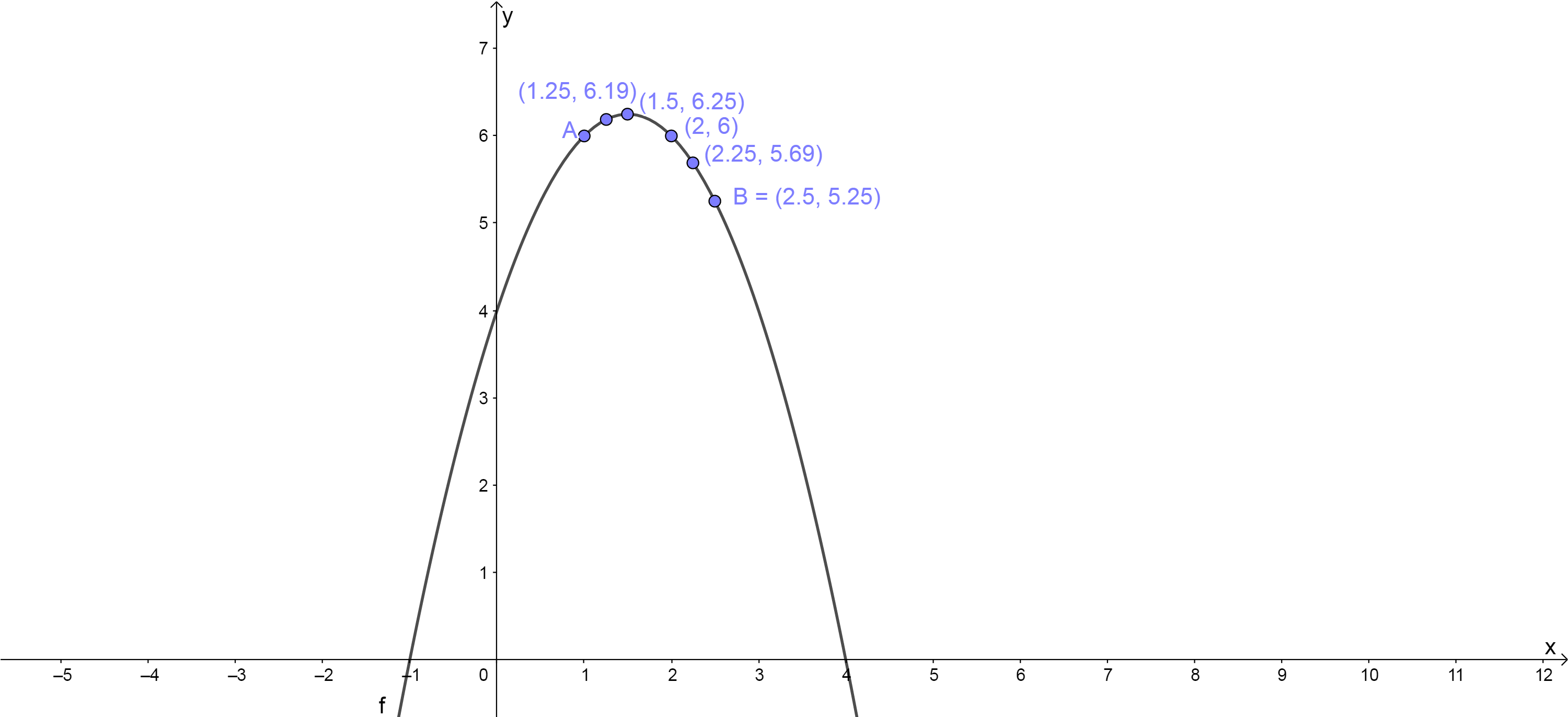
We can find the average gradient between any two points as B moves closer to A. This is shown in the following table:
| Points | Average gradient |
| [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (2.5,\text{ }5.25)[/latex] | [latex]\scriptsize \begin{align*}m&=\displaystyle \frac{{5.25-6}}{{2.5-1}}\\&=-0.5\end{align*}[/latex] |
| [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (2.25,\text{ }5.69)[/latex] | [latex]\scriptsize \begin{align*}m&=\displaystyle \frac{{5.69-6}}{{2.25-1}}\\&=-0.25\end{align*}[/latex] |
| [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (2,\text{ 6})[/latex] | [latex]\scriptsize \begin{align*}m&=\displaystyle \frac{{6-6}}{{2-1}}\\&=0\end{align*}[/latex] |
| [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (1.5,\text{ 6}\text{.25})[/latex] | [latex]\scriptsize \begin{align*}m&=\displaystyle \frac{{6.25-6}}{{1.5-1}}\\&=0.5\end{align*}[/latex] |
| [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (1.25,\text{ 6}\text{.19})[/latex] | [latex]\scriptsize \begin{align*}m&=\displaystyle \frac{{6.19-6}}{{1.25-1}}\\&=0.76\end{align*}[/latex] |
If [latex]\scriptsize h[/latex] is the distance between the x-values at point A and point B then [latex]\scriptsize h[/latex] approaches [latex]\scriptsize 0[/latex] as B moves closer and closer to A. As point B approaches point A the average gradient changes as shown in the table and graph below:
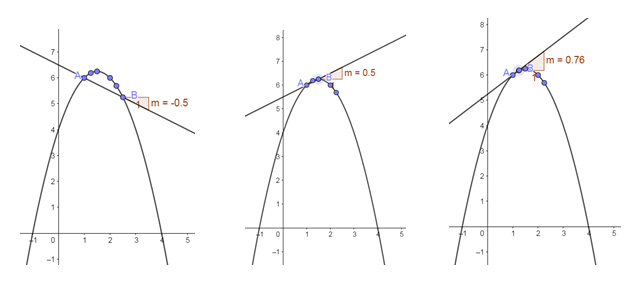
At the point where A and B overlap, the straight line passes through only one point on the curve. This line is known as a tangent to the curve. Therefore, the gradient at a point on a curve is the same as the gradient of the tangent to the curve at the given point.
We see that as point B approaches point A, [latex]\scriptsize h[/latex] gets closer to [latex]\scriptsize 0[/latex]. If point B lies on point A, then [latex]\scriptsize h=0[/latex] and the formula for average gradient is undefined.
We use our knowledge of limits to let [latex]\scriptsize h[/latex] tend to [latex]\scriptsize 0[/latex] and determine the gradient of the curve at point A. The gradient at point A as [latex]\scriptsize \underset{{h\to 0}}{\mathop{{\lim }}}\,[/latex] is given by:
[latex]\scriptsize \begin{align*}{{m}_{A}}&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{{a+h-a}}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{h}\end{align*}[/latex].
Note
When you have access to the internet you can click on this link to view an interactive graph, which shows how the gradient of the straight line through points A and B changes as B moves closer to A.
Example 1.4
Given [latex]\scriptsize f(x)=-2{{x}^{2}}[/latex], determine the gradient of the curve at point A where [latex]\scriptsize \displaystyle x=3[/latex].
Solution
The expression below is used to find the average gradient.
[latex]\scriptsize \begin{align*}\displaystyle \frac{{f(a+h)-f(a)}}{{(a+h)-a}}&=\displaystyle \frac{{-2{{{(a+h)}}^{2}}-{{{(-2a)}}^{2}}}}{h}\\&=\displaystyle \frac{{-2{{a}^{2}}-4ah-2{{h}^{2}}+2{{a}^{2}}}}{h}\\&=\displaystyle \frac{{-4ah-2{{h}^{2}}}}{h}\\&=\displaystyle \frac{{h(-4a-2h)}}{h}\\&=-4a-2h\end{align*}[/latex]
Now, to find the gradient at point A we must add in the limit.
[latex]\scriptsize {{m}_{A}}=\underset{{h\to 0}}{\mathop{{\lim }}}\,(-4a-2h)[/latex]
At point A: [latex]\scriptsize \displaystyle x=3[/latex] therefore [latex]\scriptsize a=3[/latex] as this is the point where we want to find the gradient. At that point on the curve [latex]\scriptsize h=0[/latex] so the gradient is:
[latex]\scriptsize -4(3)-2(0)=-12[/latex].
The gradient of a curve at any point is called the derivative of the function. As we have seen, the derivative of a function at a given point gives us the slope of the tangent line to the function at that point.
Example 1.5
Given the function [latex]\scriptsize f(x)=3{{x}^{2}}+x-2[/latex], determine the gradient of the tangent to the curve at the point [latex]\scriptsize \displaystyle x=1[/latex].
Solution
Step 1: Write down the formula for the gradient at a point.
[latex]\scriptsize \underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{{(a+h)-a}}[/latex]
Step 2: Find [latex]\scriptsize f(a+h)[/latex] and[latex]\scriptsize f(a)[/latex].
We need to find the gradient of the tangent to the curve at [latex]\scriptsize \displaystyle x=1[/latex], therefore we let [latex]\scriptsize \displaystyle a=1[/latex]:
[latex]\scriptsize \begin{align*}f(a+h)&=f(1+h)\\&=3{{(1+h)}^{2}}+(1+h)-2\\&=3(1+2h+{{h}^{2}})+h-1\\&=3+6h+3{{h}^{2}}+h-1\\&=3{{h}^{2}}+7h+2\end{align*}[/latex]
[latex]\scriptsize \begin{align*}f(a)&=f(1)\\&=3{{(1)}^{2}}+1-2\\&=2\end{align*}[/latex]
Step 3: Substitute into the formula and simplify.
[latex]\scriptsize \begin{align*}\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{h}&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{3{{h}^{2}}+7h+2-(2)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{3{{h}^{2}}+7h}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\cancel{h}(3h+7)}}{{\cancel{h}}}\\&=7\end{align*}[/latex]
Step 4: Write the final answer.
The gradient of the tangent to the curve [latex]\scriptsize f(x)=3{{x}^{2}}+x-2[/latex] at the point [latex]\scriptsize \displaystyle x=1[/latex] is [latex]\scriptsize 7[/latex].
Exercise 1.3
- Given [latex]\scriptsize f(x)={{x}^{2}}+x[/latex], determine the gradient of the curve at point A where [latex]\scriptsize \displaystyle x=-1[/latex].
- Given the function [latex]\scriptsize g(x)={{x}^{2}}-2[/latex], determine the gradient of the tangent to the curve at the point [latex]\scriptsize \displaystyle x=3[/latex].
The full solutions are at the end of the unit.
Differentiation from first principles
We know that the gradient of the tangent to a curve with equation [latex]\scriptsize \displaystyle y=f\left( x \right)[/latex] at [latex]\scriptsize \displaystyle x=a[/latex] can be determined using the formula: [latex]\scriptsize \underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{h}[/latex].
We can use this formula to determine an expression that describes the gradient of the graph (or the gradient of the tangent to the graph) at any point on the graph.
The derivative of a function [latex]\scriptsize \displaystyle f\left( x \right)[/latex] is written as [latex]\scriptsize {f}'(x)[/latex] and is defined as: [latex]\scriptsize {f}'(x)=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}[/latex].
We use the formula [latex]\scriptsize {f}'(x)=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}[/latex] to find the derivative of a function. This method is called differentiation from first principles, or using the definition.
Example 1.6
Calculate the derivative of [latex]\scriptsize f(x)=4x-5[/latex] from first principles.
Solution
Step 1: Write down the formula for finding the derivative using first principles.
[latex]\scriptsize {f}'(x)=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}[/latex]
Step 2: Determine[latex]\scriptsize f(x+h)[/latex].
[latex]\scriptsize \begin{align*}f(x+h)=4(x+h)-5\\=4x+4h-5\end{align*}[/latex]
Step 3: Substitute into the formula and simplify.
[latex]\scriptsize \displaystyle \begin{align*}{f}'(x)&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{4x+4h-5-(4x-5)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{4x+4h-5-4x+5}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{4h}}{h}\\&=4\end{align*}[/latex]
Step 4: Write the final answer.
[latex]\scriptsize {f}'(x)=4[/latex]
Example 1.7
Given [latex]\scriptsize f(x)=2{{x}^{3}}[/latex]:
- Find the derivative of [latex]\scriptsize f(x)[/latex].
- Determine [latex]\scriptsize {f}'(-1)[/latex] and interpret the answer.
Solutions
Step 1: Write down the formula for finding the derivative from first principles.
[latex]\scriptsize {f}'(x)=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}[/latex]
Step 2: Substitute into the formula and simplify.
[latex]\scriptsize \begin{align*}{f}'(x)&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{{(x+h)}}^{3}}-2{{x}^{3}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2({{x}^{3}}+3{{x}^{2}}h+3x{{h}^{2}}+{{h}^{3}})-2{{x}^{3}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{3}}+6{{x}^{2}}h+6x{{h}^{2}}+2{{h}^{3}}-2{{x}^{3}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{6{{x}^{2}}h+6x{{h}^{2}}+2{{h}^{3}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\cancel{h}(6{{x}^{2}}+6xh+2{{h}^{2}})}}{{\cancel{h}}}\\&=6{{x}^{2}}\end{align*}[/latex]
Step 3: Calculate [latex]\scriptsize {f}'(-1)[/latex] and interpret the answer.
[latex]\scriptsize \begin{align*}{f}'(-1)&=6{{(-1)}^{2}}\\&=6\end{align*}[/latex]
The gradient of the tangent to the curve [latex]\scriptsize f(x)[/latex] at the point [latex]\scriptsize \displaystyle x=-1[/latex] is [latex]\scriptsize 6[/latex].
OR
The gradient of the function [latex]\scriptsize f(x)[/latex] at [latex]\scriptsize \displaystyle x=-1[/latex] is [latex]\scriptsize 6[/latex].
Exercise 1.4
- Find the derivative of [latex]\scriptsize g(x)=\displaystyle \frac{1}{x}[/latex] from first principles.
- Use the definition to find [latex]\scriptsize {f}'(x)[/latex] of [latex]\scriptsize f(x)=2{{x}^{2}}-2x+1[/latex].
- Determine [latex]\scriptsize {f}'(2)[/latex] from first principles if [latex]\scriptsize f(x)=-3{{x}^{2}}[/latex].
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- How to find the limit of a function.
- How limits are applied to average gradient to find the derivative of a function.
- How to find the gradient of a curve at a point.
- How to find the derivative by using first principles.
Unit 1: Assessment
Suggested time to complete: 30 minutes
- Determine: [latex]\scriptsize \underset{{x\to -3}}{\mathop{{\lim }}}\,\displaystyle \frac{{(x+3)}}{{{{x}^{2}}-9}}[/latex].
- Determine: [latex]\scriptsize \underset{{x\to 2}}{\mathop{{\lim }}}\,\displaystyle \frac{{\sqrt{x}-\sqrt{2}}}{{x-2}}[/latex].
- Use first principles to find [latex]\scriptsize {f}'(x)[/latex] when[latex]\scriptsize f(x)=9[/latex].
- Given [latex]\scriptsize g(x)=\displaystyle \frac{2}{x}[/latex], find [latex]\scriptsize {g}'(x)[/latex]using the definition.
- Given [latex]\scriptsize f(x)=\displaystyle \frac{1}{x}-2[/latex], find [latex]\scriptsize {f}'(x)[/latex]using the definition of the derivative.
- If [latex]\scriptsize f(x)=\displaystyle \frac{1}{2}{{x}^{3}}[/latex]:
- Determine[latex]\scriptsize {f}'(x)[/latex]from first principles.
- Calculate the gradient of the tangent to [latex]\scriptsize f(x)[/latex]at the point [latex]\scriptsize x=-2[/latex].
The full solutions are at the end of the unit.
Unit 1: Solutions
Exercise 1.1
- .
[latex]\scriptsize \begin{align*}\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{h}^{2}}+4h}}{h}&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{h(h+4)}}{h}\\&=4\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{{(2+h)}}^{2}}-4}}{h}&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{4+4h+{{h}^{2}}-4}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\cancel{h}(4+h)}}{{\cancel{h}}}\\&=4\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{2}}+1}}{{{{x}^{2}}+1}}&=\underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{\displaystyle \frac{{2{{x}^{2}}}}{{{{x}^{2}}}}+\displaystyle \frac{1}{{{{x}^{2}}}}}}{{\displaystyle \frac{{{{x}^{2}}}}{{{{x}^{2}}}}+\displaystyle \frac{1}{{{{x}^{2}}}}}}\\&=\underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{2+\displaystyle \frac{1}{{{{x}^{2}}}}}}{{1+\displaystyle \frac{1}{{{{x}^{2}}}}}}\\&=\displaystyle \frac{{2+0}}{{1+0}}\\&=2\end{align*}[/latex]
(If the degree of denominator is equal to the numerator, then divide the coefficients of the terms with the highest powers.)
Exercise 1.2
Find an expression for the average gradient that you will use to answer the questions.
[latex]\scriptsize \displaystyle \begin{align*}\displaystyle \frac{{f(a+h)-f(a)}}{h}&=\displaystyle \frac{{{{{(a+h)}}^{2}}-(a+h)-2}}{h}\\&=\displaystyle \frac{{{{a}^{2}}+2ah+{{h}^{2}}-a-h-2-({{a}^{2}}-a-2)}}{h}\\&=\displaystyle \frac{{2ah+{{h}^{2}}-h}}{h}\\&=\displaystyle \frac{{\cancel{h}(2a+h-1)}}{{\cancel{h}}}\\&=2a+h-1\end{align*}[/latex]
- .
[latex]\scriptsize \displaystyle \begin{align*}\text{Average gradient}&=2(2)+3-1\\&=6\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}\text{Average gradient}&=2(5)+(-3)-1\\&=6\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}\text{Average gradient}&=2(-2)+1-1\\&=-4\end{align*}[/latex]
Exercise 1.3
- .
[latex]\scriptsize \displaystyle \begin{align*}\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{h}&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{{(h-1)}}^{2}}+(h-1)-[{{{(-1)}}^{2}}+(-1)]}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{h}^{2}}-2h+1+h-1-(0)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\cancel{h}(h-1)}}{{\cancel{h}}}\\&=-1\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{g(a+h)-g(a)}}{h}&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{{(3+h)}}^{2}}-2-[{{{(3)}}^{2}}-2]}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{9+6h+{{h}^{2}}-2-(7)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\cancel{h}(6+h)}}{{\cancel{h}}}\\&=6\end{align*}[/latex]
The gradient of the tangent to the curve at the point [latex]\scriptsize \displaystyle x=3[/latex] is [latex]\scriptsize 6[/latex].
Exercise 1.4
- .
[latex]\scriptsize \displaystyle \begin{align*}\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{g(x+h)-g(x)}}{h}&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\displaystyle \frac{1}{{x+h}}-\displaystyle \frac{1}{x}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\displaystyle \frac{{x-(x+h)}}{{x(x+h)}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\text{ }\displaystyle \frac{{x-(x+h)}}{{xh(x+h)}}\text{ Rewrite denominator}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{-\cancel{h}}}{{x\cancel{h}(x+h)}}\\&=\displaystyle \frac{{-1}}{{{{x}^{2}}}}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{{(x+h)}}^{2}}-2(x+h)+1-(2{{x}^{2}}-2x+1)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2({{x}^{2}}+2xh+{{h}^{2}})-2x-2h+1-2{{x}^{2}}+2x-1}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{2}}+4xh+2{{h}^{2}}-2h-2{{x}^{2}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{4xh+2{{h}^{2}}-2h}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\cancel{h}(4x+2h-2)}}{{\cancel{h}}}\\&=4x-2\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{-3{{{(x+h)}}^{2}}-(-3{{x}^{2}})}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{-3{{x}^{2}}-6xh-3{{h}^{2}}+3{{x}^{2}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{-6xh-3{{h}^{2}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\cancel{h}(-6x-3h)}}{{\cancel{h}}}\\&=-6x\\{f}'(2)&=-12\end{align*}[/latex]
Unit 1: Assessment
- .
[latex]\scriptsize \begin{align*}\underset{{x\to -3}}{\mathop{{\lim }}}\,\displaystyle \frac{{(x+3)}}{{{{x}^{2}}-9}}&=\underset{{x\to -3}}{\mathop{{\lim }}}\,\displaystyle \frac{{\cancel{{(x+3)}}}}{{(x-3)\cancel{{(x+3)}}}}\\&=\displaystyle \frac{1}{{-6}}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\underset{{x\to 2}}{\mathop{{\lim }}}\,\displaystyle \frac{{\sqrt{x}-\sqrt{2}}}{{x-2}}&=\underset{{x\to 2}}{\mathop{{\lim }}}\,\displaystyle \frac{{\cancel{{(\sqrt{x}-\sqrt{2})}}}}{{\cancel{{(\sqrt{x}-\sqrt{2})}}(\sqrt{x}+\sqrt{2})}}\\&=\displaystyle \frac{1}{{2\sqrt{2}}}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}{f}'(x)&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}\\&=\displaystyle \frac{{9-9}}{h}\\&=0\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}{g}'(x)&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{g(x+h)-g(x)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\displaystyle \frac{2}{{x+h}}-\displaystyle \frac{2}{x}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\displaystyle \frac{{2x-2(x+h)}}{{x(x+h)}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2x-2x-2h}}{{xh(x+h)}}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{-2}}{{x(x+h)}}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{-2}}{{{{x}^{2}}+xh}}\\&=\displaystyle \frac{{-2}}{{{{x}^{2}}}}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}{f}'(x)&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\displaystyle \frac{1}{{x+h}}-2-\left( {\displaystyle \frac{1}{x}-2} \right)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\displaystyle \frac{1}{{x+h}}-\displaystyle \frac{1}{x}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{x-x-h}}{{xh(x+h)}}\\&=\displaystyle \frac{{-1}}{{{{x}^{2}}}}\end{align*}[/latex] - .
- .
[latex]\scriptsize \displaystyle \begin{align*}{f}'(x)&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\tfrac{1}{2}({{x}^{3}}+3{{x}^{2}}h+3x{{h}^{2}}+{{h}^{3}})-\tfrac{1}{2}{{x}^{3}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\tfrac{1}{2}{{x}^{3}}+\tfrac{3}{2}{{x}^{2}}h+\tfrac{3}{2}x{{h}^{2}}+\tfrac{1}{2}{{h}^{3}}-\tfrac{1}{2}{{x}^{3}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\tfrac{3}{2}{{x}^{2}}+\tfrac{3}{2}xh+\tfrac{1}{2}{{h}^{2}}\\&=\tfrac{3}{2}{{x}^{2}}\end{align*}[/latex] - .
The gradient of the tangent to [latex]\scriptsize f(x)[/latex]at the point [latex]\scriptsize x=-2[/latex] is [latex]\scriptsize \displaystyle \tfrac{3}{2}{{(-2)}^{2}}=6[/latex].
- .
Media Attributions
- Fig 1 Avg gradient © DHET is licensed under a CC BY (Attribution) license
- Fig 2 Gradient at a point © DHET is licensed under a CC BY (Attribution) license
- Fig 3 Avg gradient changing © DHET is licensed under a CC BY (Attribution) license
