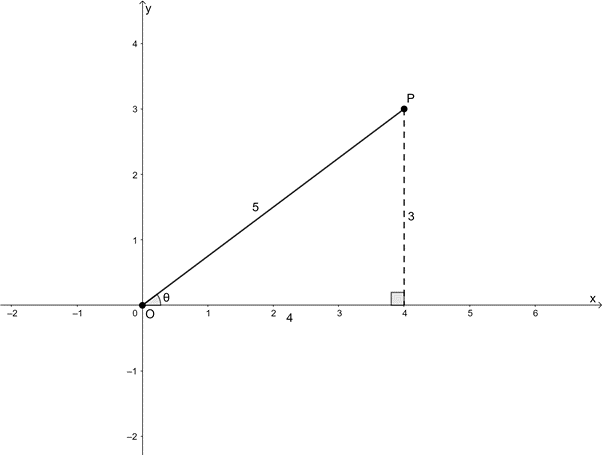Space, shape and measurement: Solve problems by constructing and interpreting trigonometric models
Unit 1: Work with compound angles
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Expand the compound angles of [latex]\scriptsize \sin (\alpha \pm \beta )[/latex] and [latex]\scriptsize \cos (\alpha \pm \beta )[/latex].
- Use the compound expansions to simplify expressions.
- Use compound angles to prove identities.
What you should know
Before you start this unit, make sure you can:
- Simplify trigonometric expressions without a calculator, by using the special angles of [latex]\scriptsize {{30}^\circ}[/latex], [latex]\scriptsize {{45}^\circ}[/latex] and [latex]\scriptsize {{60}^\circ}[/latex]. Refer to level 3 subject outcome 3.3 unit 1 if you need help with this.
- Simplify trigonometric expression using the reduction formulae of [latex]\scriptsize ({{90}^\circ}\pm \theta )[/latex], [latex]\scriptsize ({{180}^\circ}\pm \theta )[/latex] and [latex]\scriptsize ({{360}^\circ}\pm \theta )[/latex]. Refer to level 3 subject outcome 3.3 unit 2 if you need help with this.
- State and apply the basic trigonometric identities of:
- [latex]\scriptsize {{\sin }^{2}}x+{{\cos }^{2}}x=1[/latex]
- [latex]\scriptsize \tan x=\displaystyle \frac{{\sin x}}{{\cos x}}[/latex].
Refer to level 3 subject outcome 3.3 unit 3 if you need help with this.
- State and use the distance formula. Refer to level 2 subject outcome 3.3 unit 2 if you need help with this.
Introduction
There is a very important property in algebra that you have been using for many years now. It is called the distributive property of multiplication over addition (or just the distributive property). It says that the product of a number and the sum of two or more other numbers is equal to the sum of the products or that [latex]\scriptsize x(a+b)=xa+xb[/latex]. You know it well, right?
Now it might seem reasonable to apply the distributive property to an expression such as [latex]\scriptsize \cos ({{30}^\circ}+{{20}^\circ})[/latex] and say that [latex]\scriptsize \cos ({{30}^\circ}+{{20}^\circ})=\cos {{30}^\circ}+\cos {{20}^\circ}[/latex]. But is this true? Use a calculator to work out the values of the left-hand and the right-hand sides of the equation. Are they the same? Is the equation true?
You should have found that [latex]\scriptsize \cos ({{30}^\circ}+{{20}^\circ})=\cos {{50}^\circ}=0.643[/latex] (rounded to three decimal places) and that [latex]\scriptsize \cos {{30}^\circ}+\cos {{20}^\circ}=1.806[/latex] (rounded to three decimal places). The answers are not even close. Therefore, we know that:
[latex]\scriptsize \displaystyle \cos ({{30}^\circ}+{{20}^\circ})\ne \cos {{30}^\circ}+\cos {{20}^\circ}[/latex]
There is a very good reason why we cannot apply the distributive property in this case. We are not multiplying [latex]\scriptsize \cos[/latex] by [latex]\scriptsize ({{30}^\circ}+{{20}^\circ})[/latex]. Cosine is a function that we are applying to the sum of two angles. The distributive property applies only if we are finding a product (multiplying two or more numbers).
So, that leaves us with the question, ‘what is [latex]\scriptsize \cos ({{30}^\circ}+{{20}^\circ})[/latex] equal to?’. We are going to answer this question in activity 1.1.
The compound angle identities
For this next activity, we are going to use the cosine rule and the distance formula. If you don’t remember what these are, look at the references in the ‘What you should know’ section above before continuing.
Activity 1.1: What is cos(30o + 20o) equal to?
Time required: 10 minutes
What you need:
- a pen or pencil
- a blank piece of paper
- a calculator
What to do:
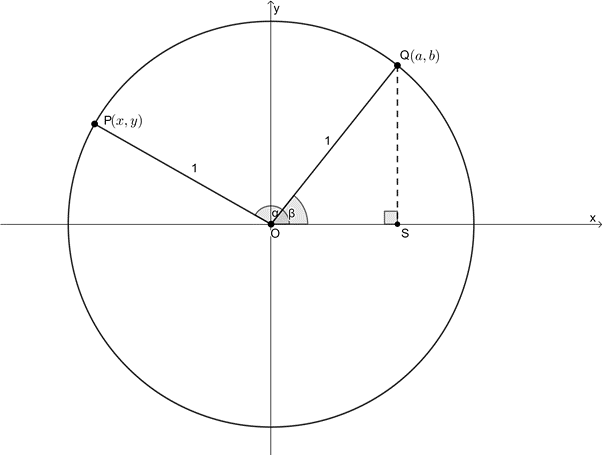
Have a look at this diagram of a unit circle on the Cartesian plane. Two points, [latex]\scriptsize P(x,y)[/latex] and [latex]\scriptsize Q(a,b)[/latex] have been drawn. [latex]\scriptsize P[/latex] is at an angle of [latex]\scriptsize \alpha[/latex] from the positive x-axis and [latex]\scriptsize Q[/latex] is at an angle of [latex]\scriptsize \beta[/latex] from the positive x-axis.
- Express the coordinates of [latex]\scriptsize Q[/latex] as trigonometric ratios.
- Express the coordinates of [latex]\scriptsize P[/latex] as trigonometric ratios. Hint: drop another perpendicular.
- Write down an expression for the distance between [latex]\scriptsize P[/latex] and [latex]\scriptsize Q[/latex] in terms of the coordinates for these points that you found in 1. and 2. Hint: Use the distance formula.
- Use this expression to find [latex]\scriptsize P{{Q}^{2}}[/latex].
- What is the angle formed between [latex]\scriptsize P[/latex] and [latex]\scriptsize Q[/latex] i.e. what is the angle [latex]\scriptsize P\hat{O}Q[/latex]?
- Write down another expression for the distance between [latex]\scriptsize P[/latex] and [latex]\scriptsize Q[/latex] but this time in terms of the included angle [latex]\scriptsize P\hat{O}Q[/latex]. Hint: Use the cosine rule.
- If both of these expressions are the distance [latex]\scriptsize PQ[/latex], write down an expression for [latex]\scriptsize \cos (\alpha -\beta )[/latex].
What did you find?
- In [latex]\scriptsize \Delta QOS[/latex], [latex]\scriptsize \sin \beta =\displaystyle \frac{{opp}}{{hyp}}=\displaystyle \frac{b}{1}[/latex]. Therefore, [latex]\scriptsize b=\sin \beta[/latex].
[latex]\scriptsize \cos \beta =\displaystyle \frac{{adj}}{{hyp}}=\displaystyle \frac{a}{1}[/latex]. Therefore, [latex]\scriptsize a=\cos \beta[/latex].
So, the coordinates of [latex]\scriptsize Q[/latex] are [latex]\scriptsize Q\left( {\cos \beta ,\sin \beta } \right)[/latex]. - We can drop a perpendicular to the x-axis from [latex]\scriptsize P[/latex], and call this point [latex]\scriptsize T[/latex].
Then in [latex]\scriptsize \Delta POT[/latex], [latex]\scriptsize \sin \alpha =\displaystyle \frac{{opp}}{{hyp}}=\displaystyle \frac{y}{1}[/latex]. Therefore, [latex]\scriptsize y=\sin \alpha[/latex].
[latex]\scriptsize \cos \alpha =\displaystyle \frac{{adj}}{{hyp}}=\displaystyle \frac{x}{1}[/latex]. Therefore, [latex]\scriptsize x=\cos \alpha[/latex].
So, the coordinates of [latex]\scriptsize P[/latex] are [latex]\scriptsize P\left( {\cos \alpha ,\sin \alpha } \right)[/latex]. - We know that the distance between two points is given by [latex]\scriptsize d=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}[/latex]. Therefore, the distance [latex]\scriptsize PQ[/latex] will be [latex]\scriptsize PQ=\sqrt{{{{{(x-a)}}^{2}}+{{{(y-b)}}^{2}}}}[/latex]. But we have trig-based expressions for all these coordinates. Therefore, [latex]\scriptsize PQ=\sqrt{{{{{(\cos \alpha -\cos \beta )}}^{2}}+{{{(\sin \alpha -\sin \beta )}}^{2}}}}[/latex]
- We need to square both sides.
[latex]\scriptsize \displaystyle \begin{align*}PQ & =\sqrt{{{{{(\cos \alpha -\cos \beta )}}^{2}}+{{{(\sin \alpha -\sin \beta )}}^{2}}}}\\\therefore P{{Q}^{2}} & ={{(\cos \alpha -\cos \beta )}^{2}}+{{(\sin \alpha -\sin \beta )}^{2}}\\&={{\cos }^{2}}\alpha -2\cos \alpha \cos \beta +{{\cos }^{2}}\beta +{{\sin }^{2}}\alpha -2\sin \alpha \sin \beta +{{\sin }^{2}}\beta \\&=({{\cos }^{2}}\alpha +{{\sin }^{2}}\alpha )+({{\cos }^{2}}\beta +{{\sin }^{2}}\beta )-2\cos \alpha \cos \beta -2\sin \alpha \sin \beta \\&=1+1-2(\cos \alpha \cos \beta +\sin \alpha \sin \beta )\quad (\text{Remember that }{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1)\\&=2-2(\cos \alpha \cos \beta +\sin \alpha \sin \beta )\end{align*}[/latex] - [latex]\scriptsize P\hat{O}Q=\alpha -\beta[/latex]
- The cosine rule states that [latex]\scriptsize {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\cos A[/latex] where [latex]\scriptsize a[/latex] is the side opposite [latex]\scriptsize \hat{A}[/latex]. In our case, [latex]\scriptsize PQ[/latex] is the side opposite [latex]\scriptsize (\alpha -\beta )[/latex] in [latex]\scriptsize \Delta PQO[/latex]. Therefore: [latex]\scriptsize P{{Q}^{2}}=P{{O}^{2}}+Q{{O}^{2}}-2PO\cdot QO\cos (\alpha -\beta )[/latex]. But both [latex]\scriptsize PO[/latex] and [latex]\scriptsize QO[/latex] are equal to [latex]\scriptsize 1[/latex]. Therefore:
[latex]\scriptsize \begin{align*}P{{Q}^{2}}&=P{{O}^{2}}+Q{{O}^{2}}-2PO\cdot QO\cos (\alpha -\beta )\\&=1+1-2(1)(1)\cos (\alpha -\beta )\\&=2-2\cos (\alpha -\beta )\end{align*}[/latex] - We can now equate our two expressions and then rearrange the equation to get [latex]\scriptsize \cos (\alpha -\beta )[/latex] on the one side.
[latex]\scriptsize \begin{align*}P{{Q}^{2}} & =2-2(\cos \alpha \cos \beta +\sin \alpha \sin \beta )=2-2\cos (\alpha -\beta )\\\therefore 2\cos (\alpha -\beta ) & =2(\cos \alpha \cos \beta +\sin \alpha \sin \beta )\\\therefore \cos (\alpha -\beta ) & =(\cos \alpha \cos \beta +\sin \alpha \sin \beta )\end{align*}[/latex]
We now have an expression for [latex]\scriptsize \cos (\alpha -\beta )[/latex], the cosine of the compound angle [latex]\scriptsize \alpha -\beta[/latex], in terms of trig ratios of the single angles [latex]\scriptsize \alpha[/latex] and [latex]\scriptsize \beta[/latex].
[latex]\scriptsize \cos (\alpha -\beta ) =(\cos \alpha \cos \beta +\sin \alpha \sin \beta )[/latex].
Notice that the signs are different. There is a negative on the left-hand side but a positive on the right-hand side.
What do you think [latex]\scriptsize \cos (\alpha +\beta )[/latex] is equal to? Try figure this out on your own by using the fact that [latex]\scriptsize \cos (\alpha +\beta )=\cos \left( {\alpha -(-\beta )} \right)[/latex].
Does your reasoning agree with the following?
[latex]\scriptsize \cos \left( {\alpha -(-\beta )} \right)=\cos \alpha \cos (-\beta )+\sin \alpha \sin (-\beta )[/latex]. But we know that [latex]\scriptsize \cos (-\beta )=\cos \beta[/latex] and [latex]\scriptsize \sin (-\beta )=-\sin \beta[/latex].
Therefore:
[latex]\scriptsize \begin{align*}\cos \left( {\alpha -(-\beta )} \right)&=\cos \alpha \cos (-\beta )+\sin \alpha \sin (-\beta )\\&=\cos \alpha \cos \beta +\sin \alpha (-\sin \beta )\\&=\cos \alpha \cos \beta -\sin \alpha \sin \beta \end{align*}[/latex]
Don’t you love the symmetry?
[latex]\scriptsize \cos (\alpha -\beta ) =(\cos \alpha \cos \beta +\sin \alpha \sin \beta )[/latex]
[latex]\scriptsize \cos (\alpha +\beta ) =(\cos \alpha \cos \beta -\sin \alpha \sin \beta )[/latex]
We call these the cosine compound angle identities.
Now, we can use these identities to work out identities that express [latex]\scriptsize \sin (\alpha -\beta )[/latex] and [latex]\scriptsize \sin (\alpha +\beta )[/latex] in terms of trig ratios of the single angles [latex]\scriptsize \alpha[/latex] and [latex]\scriptsize \beta[/latex]. On your own, use the fact that [latex]\scriptsize \sin \theta =\cos ({{90}^\circ}-\theta )[/latex], combined with the [latex]\scriptsize \cos (\alpha +\beta )[/latex] identity, to work out an identity that expresses [latex]\scriptsize \sin (\alpha -\beta )[/latex] in terms of trig ratios of the single angles [latex]\scriptsize \alpha[/latex] and [latex]\scriptsize \beta[/latex].
[latex]\scriptsize \begin{align*}\sin (\alpha -\beta )&=\cos \left( {{{{90}}^\circ}-(\alpha -\beta )} \right)\\&=\cos \left( {({{{90}}^\circ}-\alpha )+\beta )} \right)\\&=\cos ({{90}^\circ}-\alpha )\cos \beta -\sin ({{90}^\circ}-\alpha )\sin \beta \\&=\sin \alpha \cos \beta -\cos \alpha \sin \beta \end{align*}[/latex]
Now, use the [latex]\scriptsize \sin (\alpha -\beta )[/latex] identity to work out a similar identity for [latex]\scriptsize \sin (\alpha +\beta )[/latex].
[latex]\scriptsize \begin{align*}\sin (\alpha +\beta )&=\sin \left( {\alpha -(-\beta )} \right)\\&=\sin \alpha \cos (-\beta )-\cos \alpha \sin (-\beta )\\&=\sin \alpha \cos (\beta )-\cos \alpha (-\sin \beta )\\&=\sin \alpha \cos \beta +\cos \alpha \sin \beta \end{align*}[/latex]
Compound angle identities:
[latex]\scriptsize \sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta[/latex]
[latex]\scriptsize \sin (\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta[/latex]
For sine, the signs are the same but the ratios in each term are different.
[latex]\scriptsize \cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta[/latex]
[latex]\scriptsize \cos (\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta[/latex]
For cosine, the signs are different but the ratios in each term are the same.
Example 1.1
Determine [latex]\scriptsize \cos {{75}^\circ}[/latex] without a calculator.
Solution
Whenever you see a trigonometry question state that you must not use a calculator, you know that you need to use the special angles.
We know that [latex]\scriptsize {{75}^\circ}={{45}^\circ}+{{30}^\circ}[/latex]. Therefore, we can use a compound angle identity to rewrite [latex]\scriptsize \cos {{75}^\circ}[/latex] with special angles and calculate its value without a calculator.
[latex]\scriptsize \displaystyle \begin{align*}\cos {{75}^\circ}&=\cos ({{45}^\circ}+{{30}^\circ})\\&=\cos {{45}^\circ}\cos {{30}^\circ}-\sin {{45}^\circ}\sin {{30}^\circ}\\&=\displaystyle \frac{1}{{\sqrt{2}}}\times \displaystyle \frac{{\sqrt{3}}}{2}-\displaystyle \frac{1}{{\sqrt{2}}}\times \displaystyle \frac{1}{2}\\&=\displaystyle \frac{{\sqrt{3}}}{{2\sqrt{2}}}-\displaystyle \frac{1}{{2\sqrt{2}}}\\&=\displaystyle \frac{{\sqrt{3}-1}}{{2\sqrt{2}}}\quad \quad \text{Multiply by }\displaystyle \frac{{\sqrt{2}}}{{\sqrt{2}}}\\&=\displaystyle \frac{{\sqrt{2}\left( {\sqrt{3}-1} \right)}}{4}\end{align*}[/latex]
Example 1.2
Determine the value of the following expression without the use of a calculator.
[latex]\scriptsize \displaystyle \cos {{65}^\circ}\cos {{35}^\circ}+\cos {{25}^\circ}\cos {{55}^\circ}[/latex]
Solution
Once again, we are told that a calculator must not be used. Therefore, we need to rely on special angles. Unfortunately, as it stands, the expression does not match any of our compound angle identities. When this is the case, it is often a good idea to change sine into cosine, or vice versa. In this case, let’s use the fact that [latex]\scriptsize \cos {{65}^\circ}=\cos ({{90}^\circ}-{{25}^\circ})=\sin {{25}^\circ}[/latex] and [latex]\scriptsize \cos {{55}^\circ}=\cos ({{90}^\circ}-{{35}^\circ})=\sin {{35}^\circ}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}\cos {{65}^\circ}\cos {{35}^\circ}+\cos {{25}^\circ}\cos {{55}^\circ}&=\cos ({{90}^\circ}-{{25}^\circ})\cos {{35}^\circ}+\cos {{25}^\circ}\cos ({{90}^\circ}-{{35}^\circ})\\&=\sin {{25}^\circ}\cos {{35}^\circ}+\cos {{25}^\circ}\sin {{35}^\circ}\end{align*}[/latex]
Now we have an expression that does match one of the compound angle identities:
[latex]\scriptsize \sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta[/latex] where [latex]\scriptsize \displaystyle \alpha ={{25}^\circ}[/latex] and [latex]\scriptsize \beta ={{35}^\circ}[/latex].
[latex]\scriptsize \displaystyle \begin{align*}\sin {{25}^\circ}\cos {{35}^\circ}+\cos {{25}^\circ}\sin {{35}^\circ}&=\sin ({{25}^\circ}+{{35}^\circ})\\&=\sin {{60}^\circ}\\&=\displaystyle \frac{{\sqrt{3}}}{2}\end{align*}[/latex]
Exercise 1.1
- Calculate the value of the following without using a calculator:
- [latex]\scriptsize \cos {{105}^\circ}[/latex]
- [latex]\scriptsize \sin {{15}^\circ}[/latex]
- Determine the value of the following expressions without using a calculator:
- [latex]\scriptsize \sin {{10}^\circ}\cos {{20}^\circ}+\cos {{10}^\circ}\sin {{20}^\circ}[/latex]
- [latex]\scriptsize \cos {{50}^\circ}\sin {{80}^\circ}-\cos {{40}^\circ}\sin {{10}^\circ}[/latex]
- [latex]\scriptsize {{\cos }^{2}}{{15}^\circ}-{{\sin }^{2}}{{15}^\circ}[/latex]
- [latex]\scriptsize \sin x\cos ({{30}^\circ}+x)-\cos x\sin ({{30}^\circ}+x)[/latex]
Question 3 adapted from Everything Maths Grade 12 Exercise 4-2 question 3
- .
- Prove that [latex]\scriptsize \sin ({{60}^\circ}-x)+\sin ({{60}^\circ}+x)=\sqrt{3}\cos x[/latex].
- Hence, evaluate [latex]\scriptsize \sin {{15}^\circ}+\sin {{105}^\circ}[/latex] without a calculator.
- Simplify the following expression without a calculator:
[latex]\scriptsize \displaystyle \frac{{\sin x\cos ({{{30}}^\circ}+x)-\cos x\sin ({{{30}}^\circ}+x)}}{{\cos x\cos ({{{60}}^\circ}+x)+\sin x\sin ({{{60}}^\circ}+x)}}[/latex]
The full solutions are at the end of the unit.
Double angle identities
The double angle identities [latex]\scriptsize \sin 2\theta[/latex] and [latex]\scriptsize \cos 2\theta[/latex]are special cases of the compound angle identities [latex]\scriptsize \sin (\alpha +\beta )[/latex] and [latex]\scriptsize \cos (\alpha +\beta )[/latex]. You should be able to derive these identities yourself. Try doing this now before reading on.
Here are the derivations for you to check your own work.
[latex]\scriptsize \begin{align*}\sin 2\theta &=\sin (\theta +\theta )\\&=\sin \theta \cos \theta +\cos \theta \sin \theta \\&=2\sin \theta \cos \theta \end{align*}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}\cos 2\theta &=\cos (\theta +\theta )\\&=\cos \theta \cos \theta -\sin \theta \sin \theta \\&={{\cos }^{2}}\theta -{{\sin }^{2}}\theta \end{align*}[/latex]
Remember that [latex]\scriptsize {{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1[/latex]. Therefore, we can write two more alternative versions of the cosine double angle identity.
[latex]\scriptsize \displaystyle \begin{align*}{{\cos }^{2}}\theta -{{\sin }^{2}}\theta &=(1-{{\sin }^{2}}\theta )-{{\sin }^{2}}\theta \\&=1-2{{\sin }^{2}}\theta \end{align*}[/latex]
Or
[latex]\scriptsize \displaystyle \begin{align*}{{\cos }^{2}}\theta -{{\sin }^{2}}\theta &={{\cos }^{2}}\theta -(1-{{\cos }^{2}}\theta )\\&=2{{\cos }^{2}}\theta -1\end{align*}[/latex]
Double angle identities:
[latex]\scriptsize \sin 2\theta =2\sin \theta \cos \theta[/latex]
[latex]\scriptsize \cos 2\theta =\left\{ \begin{align*}{{\cos }^{2}}\theta -{{\sin }^{2}}\theta \\2{{\cos }^{2}}\theta -1\\1-2{{\sin }^{2}}\theta \end{align*} \right\}[/latex]
Example 1.3
If [latex]\scriptsize {{0}^\circ}\le \theta \le {{90}^\circ}[/latex] and [latex]\scriptsize \tan \theta =0.75[/latex], determine the value of [latex]\scriptsize \sin 2\theta[/latex] without using a calculator.
Solution
We know that [latex]\scriptsize \theta[/latex] is an acute angle in the first quadrant. We also know that [latex]\scriptsize \tan \theta =0.75=\displaystyle \frac{3}{4}[/latex]. We can use Pythagoras to find the length of the hypotenuse.
Now we need to determine [latex]\scriptsize \sin 2\theta[/latex]:
[latex]\scriptsize \begin{align*}\sin 2\theta &=2\sin \theta \cos \theta \\&=2\times \displaystyle \frac{3}{5}\times \displaystyle \frac{4}{5}\\&=\displaystyle \frac{{24}}{{25}}\end{align*}[/latex]
Often, we use the double angle identities to simplify more complicated expressions as shown in example 1.4.
Example 1.4
Prove that [latex]\scriptsize \displaystyle \frac{{1+\cos 2\theta +\cos \theta }}{{\sin \theta +\sin 2\theta }}=\displaystyle \frac{1}{{\tan \theta }}[/latex].
Solution
It is usually a good idea to start by trying to simplify the more complicated side of the expression to see if you can get to the less complicated expression. In this case, the LHS is the more complicated side. Often, you will need to play around with various options to find the one that works. Don’t give up if your first idea does not work.
[latex]\scriptsize \displaystyle \begin{align*}\text{LHS}&=\displaystyle \frac{{1+\cos 2\theta +\cos \theta }}{{\sin \theta +\sin 2\theta }}\\&=\displaystyle \frac{{1+{{{\sin }}^{2}}\theta -{{{\cos }}^{2}}\theta +\cos \theta }}{{\sin \theta +2\sin \theta \cos \theta }}\quad \quad \text{Try another cosine double angle identity}\\&=\displaystyle \frac{{1+(2{{{\cos }}^{2}}\theta -1)+\cos \theta }}{{\sin \theta (1+2\cos \theta )}}\\&=\displaystyle \frac{{2{{{\cos }}^{2}}\theta +\cos \theta }}{{\sin \theta (1+2\cos \theta )}}\\&=\displaystyle \frac{{\cos \theta (2\cos \theta +1)}}{{\sin \theta (1+2\cos \theta )}}\\&=\displaystyle \frac{{\cos \theta (1+2\cos \theta )}}{{\sin \theta (1+2\cos \theta )}}\\&=\displaystyle \frac{{\cos \theta }}{{\sin \theta }}\\&=\displaystyle \frac{1}{{\tan \theta }}=\text{RHS}\end{align*}[/latex]
Example 1.5
Given that [latex]\scriptsize \cos {{75}^\circ}=a[/latex], determine the following in terms of [latex]\scriptsize a[/latex] without using a calculator.
- [latex]\scriptsize \cos {{150}^\circ}[/latex]
- [latex]\scriptsize \sin {{165}^\circ}[/latex]
- [latex]\scriptsize \sin {{75}^\circ}[/latex]
Solutions
- This first question is straight forward. We can simply apply the cosine double angle identity.
[latex]\scriptsize \begin{align*}\cos {{150}^\circ}&=\cos ({{75}^\circ}+{{75}^\circ})\\&=2{{\cos }^{2}}{{75}^\circ}-1\\&=2{{a}^{2}}-1\end{align*}[/latex] - This question does not need us to apply any double angle identity.
[latex]\scriptsize \begin{align*}\sin {{165}^\circ}&=\sin ({{90}^\circ}+{{75}^\circ})\\&=\cos {{75}^\circ}\\&=a\end{align*}[/latex] - This is a tricky question. We need to express [latex]\scriptsize \sin {{150}^\circ}[/latex] in terms of [latex]\scriptsize a=\cos {{75}^\circ}[/latex] so we cannot use either the fact that [latex]\scriptsize \sin {{150}^\circ}=\sin ({{180}^\circ}-{{30}^\circ})[/latex] or [latex]\scriptsize \sin {{150}^\circ}=\sin ({{90}^\circ}+{{60}^\circ})[/latex] directly. We need to apply the double angle identity in reverse. We know that:
[latex]\scriptsize \begin{align*}\sin {{150}^\circ}&=\sin ({{75}^\circ}+{{75}^\circ})\\&=2\sin {{75}^\circ}\cos {{75}^\circ}\end{align*}[/latex]
.
We already know that [latex]\scriptsize \cos {{75}^\circ}=a[/latex] but in order to find an expression for [latex]\scriptsize \sin {{75}^\circ}[/latex] we need to determine the value of [latex]\scriptsize \sin {{150}^\circ}[/latex]. Thankfully, we can easily do this without a calculator.
[latex]\scriptsize \begin{align*}\sin {{150}^\circ}&=\sin ({{180}^\circ}-{{30}^\circ})\\&=\sin {{30}^\circ}\\&=\displaystyle \frac{1}{2}\end{align*}[/latex]
Now we can say that:
[latex]\scriptsize \begin{align*}2\sin {{75}^\circ}\cos {{75}^\circ} & =\displaystyle \frac{1}{2}\\\therefore \sin {{75}^\circ}\cos {{75}^\circ} & =\displaystyle \frac{1}{4}\\\text{But }\cos {{75}^\circ} & =a\\\therefore \sin {{75}^\circ} & =\displaystyle \frac{1}{{4a}}\end{align*}[/latex]
Exercise 1.2
- Given [latex]\scriptsize \sin {{50}^\circ}=a[/latex] and [latex]\scriptsize \sin {{40}^\circ}=b[/latex], determine the value of the following in terms of [latex]\scriptsize a[/latex] and [latex]\scriptsize b[/latex]:
- [latex]\scriptsize \sin {{100}^\circ}[/latex]
- [latex]\scriptsize \cos {{40}^\circ}[/latex]
- [latex]\scriptsize \cos {{140}^\circ}[/latex]
- [latex]\scriptsize \cos {{25}^\circ}[/latex]
- [latex]\scriptsize \cos {{80}^\circ}[/latex]
- [latex]\scriptsize \cos (-{{800}^\circ})[/latex]
Question 2 adapted from Everything Maths Grade 12 Exercise 4-3 question 3
- Prove the following identity:
[latex]\scriptsize \displaystyle \frac{1}{{\sin 2A}}-\displaystyle \frac{1}{{\tan 2A}}=\tan A[/latex] - Given [latex]\scriptsize 13\cos \theta =-5[/latex] and [latex]\scriptsize {{180}^\circ}\le \theta \le {{360}^\circ}[/latex], determine the value of the following expressions without a calculator:
- [latex]\scriptsize \cos 2\theta[/latex]
- [latex]\scriptsize \sin 2\theta[/latex]
- [latex]\scriptsize \tan 4\theta[/latex]
- [latex]\scriptsize \sin ({{180}^\circ}-2\theta )[/latex]
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- [latex]\scriptsize \sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta[/latex]
- [latex]\scriptsize \sin (\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta[/latex]
- [latex]\scriptsize \cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta[/latex]
- [latex]\scriptsize \cos (\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta[/latex]
- [latex]\scriptsize \sin 2\theta =2\sin \theta \cos \theta[/latex]
- [latex]\scriptsize \cos 2\theta =\left\{ \begin{align*}&{{\cos }^{2}}\theta -{{\sin }^{2}}\theta \\&2{{\cos }^{2}}\theta -1\\&1-2{{\sin }^{2}}\theta \end{align*} \right\}[/latex]
Unit 1: Assessment
Suggested time to complete: 60 minutes
- Prove that [latex]\scriptsize \sin {{75}^\circ}+\sin {{15}^\circ}=\displaystyle \frac{{\sqrt{6}}}{2}[/latex].
- Prove that [latex]\scriptsize \displaystyle \frac{{\sin 2\theta }}{{\sin \theta }}-\displaystyle \frac{{\cos 2\theta }}{{\cos \theta }}=\displaystyle \frac{1}{{\cos \theta }}[/latex].
- Given that [latex]\scriptsize \cos \theta =a[/latex], determine [latex]\scriptsize \cos 3\theta[/latex] in terms of [latex]\scriptsize a[/latex].
- .
- Prove that [latex]\scriptsize \sin (S+T)-\sin (S-T)=2\cos S\sin T[/latex].
- Hence, calculate the value of [latex]\scriptsize \cos {{15}^\circ}\sin {{75}^\circ}[/latex] without a calculator.
- .
- Prove that [latex]\scriptsize \tan 2x+\displaystyle \frac{1}{{\cos 2x}}=\displaystyle \frac{{\sin x+\cos x}}{{\cos x-\sin x}}[/latex].
- Explain why the identity is undefined for [latex]\scriptsize x={{45}^\circ}[/latex].
- Determine the value of [latex]\scriptsize \cos {{67.5}^\circ}[/latex] without a calculator.
Question 7 adapted from NC(V) Level 4 November 2011 Paper 2 question 3.3
- Prove that [latex]\scriptsize \sin (A+B)\times \sin (A-B)={{\sin }^{2}}A-{{\sin }^{2}}B[/latex].
Question 8 and 9 adapted from NC(V) Level 4 November 2012 Paper 2 question 3.3 and 3.4
- If [latex]\scriptsize {{90}^\circ} \lt A \lt {{360}^\circ}[/latex] and [latex]\scriptsize \tan A=\displaystyle \frac{3}{2}[/latex] show, without the use of calculator that [latex]\scriptsize \cos 2A-\sin 2A=-\displaystyle \frac{{17}}{{13}}[/latex].
- Prove that [latex]\scriptsize \cos (A+B)-\cos (A-B)=-2\sin A\sin B[/latex].
The full solutions are at the end of the unit
Unit 1: Solutions
Exercise 1.1
- .
- .
[latex]\scriptsize \begin{align*}\cos {{105}^\circ}&=\cos ({{60}^\circ}+{{45}^\circ})\\&=\cos {{60}^\circ}\cos {{45}^\circ}-\sin {{60}^\circ}\sin {{45}^\circ}\\&=\displaystyle \frac{1}{2}\cdot \displaystyle \frac{1}{{\sqrt{2}}}-\displaystyle \frac{{\sqrt{3}}}{2}\cdot \displaystyle \frac{1}{{\sqrt{2}}}\\&=\displaystyle \frac{1}{{2\sqrt{2}}}-\displaystyle \frac{{\sqrt{3}}}{{2\sqrt{2}}}\\&=\displaystyle \frac{{1-\sqrt{3}}}{{2\sqrt{2}}}\\&=\displaystyle \frac{{\sqrt{2}\left( {1-\sqrt{3}} \right)}}{4}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\sin {{15}^\circ}&=\sin ({{45}^\circ}-{{30}^\circ})\\&=\sin {{45}^\circ}\cos {{30}^\circ}-\cos {{45}^\circ}\sin {{30}^\circ}\\&=\displaystyle \frac{1}{{\sqrt{2}}}\cdot \displaystyle \frac{{\sqrt{3}}}{2}-\displaystyle \frac{1}{{\sqrt{2}}}\cdot \displaystyle \frac{1}{2}\\&=\displaystyle \frac{{\sqrt{3}}}{{2\sqrt{2}}}-\displaystyle \frac{1}{{2\sqrt{2}}}\\&=\displaystyle \frac{{\sqrt{3}-1}}{{2\sqrt{2}}}\\&=\displaystyle \frac{{\sqrt{2}\left( {\sqrt{3}-1} \right)}}{4}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}\tan {{15}^\circ}&=\displaystyle \frac{{\sin {{{15}}^\circ}}}{{\cos {{{15}}^\circ}}}\\&=\displaystyle \frac{{\sin ({{{45}}^\circ}-{{{30}}^\circ})}}{{\cos ({{{45}}^\circ}-{{{30}}^\circ})}}\\&=\displaystyle \frac{{\displaystyle \frac{{\sqrt{2}\left( {\sqrt{3}-1} \right)}}{4}}}{{\cos {{{45}}^\circ}\cos {{{30}}^\circ}+\sin {{{45}}^\circ}\sin {{{30}}^\circ}}}\quad \quad \text{See part b}\text{. for numerator calculations}\\&=\displaystyle \frac{{\displaystyle \frac{{\sqrt{2}\left( {\sqrt{3}-1} \right)}}{4}}}{{\displaystyle \frac{1}{{\sqrt{2}}}\cdot \displaystyle \frac{{\sqrt{3}}}{2}+\displaystyle \frac{1}{{\sqrt{2}}}\cdot \displaystyle \frac{1}{2}}}\\&=\displaystyle \frac{{\displaystyle \frac{{\sqrt{2}\left( {\sqrt{3}-1} \right)}}{4}}}{{\displaystyle \frac{{\sqrt{3}}}{{2\sqrt{2}}}+\displaystyle \frac{1}{{2\sqrt{2}}}}}\\&=\displaystyle \frac{{\displaystyle \frac{{\sqrt{2}\left( {\sqrt{3}-1} \right)}}{4}}}{{\displaystyle \frac{{\sqrt{3}+1}}{{2\sqrt{2}}}}}\\&=\displaystyle \frac{{\displaystyle \frac{{\sqrt{2}\left( {\sqrt{3}-1} \right)}}{4}}}{{\displaystyle \frac{{\sqrt{2}\left( {\sqrt{3}+1} \right)}}{4}}}\\&=\displaystyle \frac{{\sqrt{2}\left( {\sqrt{3}-1} \right)}}{4}\times \displaystyle \frac{4}{{\sqrt{2}\left( {\sqrt{3}+1} \right)}}\\&=\displaystyle \frac{{\left( {\sqrt{3}-1} \right)}}{{\left( {\sqrt{3}+1} \right)}}\end{align*}[/latex]
- .
- .
- .
[latex]\scriptsize \begin{align*}\sin {{10}^\circ}\cos {{20}^\circ}+\cos {{10}^\circ}\sin {{20}^\circ}&=\sin ({{10}^\circ}+{{20}^\circ})\\&=\sin {{30}^\circ}\\&=\displaystyle \frac{1}{2}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\cos {{50}^\circ}\sin {{80}^\circ}-\cos {{40}^\circ}\sin {{10}^\circ}&=\cos {{50}^\circ}\sin ({{90}^\circ}-{{10}^\circ})-\cos ({{90}^\circ}-{{50}^\circ})\sin {{10}^\circ}\\&=\cos {{50}^\circ}\cos {{10}^\circ}-\sin {{50}^\circ}\sin {{10}^\circ}\\&=\cos ({{50}^\circ}+{{10}^\circ})\\&=\cos {{60}^\circ}\\&=\displaystyle \frac{1}{2}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{\cos }^{2}}{{15}^\circ}-{{\sin }^{2}}{{15}^\circ}&=\cos {{15}^\circ}\cos {{15}^\circ}-\sin {{15}^\circ}\sin {{15}^\circ}\\&=\cos ({{15}^\circ}+{{15}^\circ})\\&=\cos {{30}^\circ}\\&=\displaystyle \frac{{\sqrt{3}}}{2}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\sin x\cos ({{30}^\circ}+x)-\cos x\sin ({{30}^\circ}+x)&=\sin \left[ {x-({{{30}}^\circ}+x)} \right]\\&=\sin (x-{{30}^\circ}-x)\\&=\sin (-{{30}^\circ})\\&=-\sin {{30}^\circ}\\&=-\displaystyle \frac{1}{2}\end{align*}[/latex]
- .
- .
- .
[latex]\scriptsize \begin{align*}\text{LHS}&=\sin ({{60}^\circ}-x)+\sin ({{60}^\circ}+x)\\&=\left( {\sin {{{60}}^\circ}\cos x-\cos {{{60}}^\circ}\sin x} \right)+\left( {\sin {{{60}}^\circ}\cos x+\cos {{{60}}^\circ}\sin x} \right)\\&=\sin {{60}^\circ}\cos x+\sin {{60}^\circ}\cos x\\&=2\times \sin {{60}^\circ}\cos x\\&=2\times \displaystyle \frac{{\sqrt{3}}}{2}\cos x\\&=\sqrt{3}\cos x=\text{RHS}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}\sin {{15}^\circ}+\sin {{105}^\circ} & =\sin ({{60}^\circ}-{{45}^\circ})+\sin ({{60}^\circ}+{{45}^\circ})\\\text{But }\sin ({{60}^\circ}-x) & +\sin ({{60}^\circ}+x)=\sqrt{3}\cos x\\\therefore \text{Let }x & ={{45}^\circ}\\\sin ({{60}^\circ}-{{45}^\circ})+\sin ({{60}^\circ}+{{45}^\circ}) & =\sqrt{3}\cos {{45}^\circ}\\&=\sqrt{3}\times \displaystyle \frac{1}{{\sqrt{2}}}\\&=\displaystyle \frac{{\sqrt{3}}}{{\sqrt{2}}}\end{align*}[/latex]
- .
- .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin x\cos ({{{30}}^\circ}+x)-\cos x\sin ({{{30}}^\circ}+x)}}{{\cos x\cos ({{{60}}^\circ}+x)+\sin x\sin ({{{60}}^\circ}+x)}}&=\displaystyle \frac{{\sin \left[ {x-\left( {{{{30}}^\circ}+x} \right)} \right]}}{{\cos \left[ {x-\left( {{{{60}}^\circ}+x} \right)} \right]}}\\&=\displaystyle \frac{{\sin (x-{{{30}}^\circ}-x)}}{{\cos (x-{{{60}}^\circ}-x)}}\\&=\displaystyle \frac{{\sin (-{{{30}}^\circ})}}{{\cos (-{{{60}}^\circ})}}\\&=\displaystyle \frac{{-\sin {{{30}}^\circ}}}{{\cos {{{60}}^\circ}}}\\&=\displaystyle \frac{{-\displaystyle \frac{1}{2}}}{{\displaystyle \frac{1}{2}}}\\&=-1\end{align*}[/latex]
Exercise 1.2
- .
- .
[latex]\scriptsize \begin{align*}\sin {{100}^\circ}&=\sin ({{50}^\circ}+{{50}^\circ})\\&=2\sin {{50}^\circ}\cos {{50}^\circ}\\&=2a\cos ({{90}^\circ}-{{40}^\circ})\\&=2a\sin {{40}^\circ}\\&=2ab\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\cos {{40}^\circ}&=\cos ({{90}^\circ}-{{50}^\circ})\\&=\sin {{50}^\circ}\\&=a\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\cos {{140}^\circ}&=\cos ({{180}^\circ}-{{40}^\circ})\\&=-\cos {{40}^\circ}\\&=-\left[ {\cos ({{{90}}^\circ}-{{{50}}^\circ})} \right]\\&=-\sin {{50}^\circ}\\&=-a\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\cos {{50}^\circ} & =\cos ({{25}^\circ}+{{25}^\circ})\\=2{{\cos }^{2}}{{25}^\circ}-1\\\therefore 2{{\cos }^{2}}{{25}^\circ} & =\cos {{50}^\circ}+1\\\therefore {{\cos }^{2}}{{25}^\circ} & =\displaystyle \frac{{\cos {{{50}}^\circ}+1}}{2}\\\therefore \cos {{25}^\circ} & =\sqrt{{\displaystyle \frac{{\cos {{{50}}^\circ}+1}}{2}}}\quad \quad \cos {{25}^\circ} \gt 0\therefore {{\cos }^{2}}{{25}^\circ} \gt 0\\&=\sqrt{{\displaystyle \frac{{\cos ({{{90}}^\circ}-{{{40}}^\circ})+1}}{2}}}\\&=\sqrt{{\displaystyle \frac{{\sin {{{40}}^\circ}+1}}{2}}}\\&=\sqrt{{\displaystyle \frac{{b+1}}{2}}}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\cos {{80}^\circ}&=\cos ({{40}^\circ}+{{40}^\circ})\\&=1-2{{\sin }^{2}}{{40}^\circ}\\&=1-2{{b}^{2}}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\cos (-{{800}^\circ})&=\cos (-{{80}^\circ}-2\cdot {{360}^\circ})\\&=\cos (-{{80}^\circ})\\&=\cos {{80}^\circ}\\&=1-2{{b}^{2}}\quad \quad \text{From e}\text{.}\end{align*}[/latex]
- .
- .
[latex]\scriptsize \begin{align*}\text{LHS}&=\displaystyle \frac{1}{{\sin 2A}}-\displaystyle \frac{1}{{\tan 2A}}\\&=\displaystyle \frac{1}{{\sin 2A}}-\displaystyle \frac{{\cos 2A}}{{\sin 2A}}\\&=\displaystyle \frac{{1-\cos 2A}}{{\sin 2A}}\\&=\displaystyle \frac{{1-(1-2{{{\sin }}^{2}}A)}}{{2\sin A\cos A}}\\&=\displaystyle \frac{{2{{{\sin }}^{2}}A}}{{2\sin A\cos A}}\\&=\displaystyle \frac{{\sin A}}{{\cos A}}\\&=\tan A=\text{RHS}\end{align*}[/latex] - [latex]\scriptsize 13\cos \theta =-5[/latex] and [latex]\scriptsize {{180}^\circ}\le \theta \le {{360}^\circ}[/latex]

- .
[latex]\scriptsize \begin{align*}\cos \theta & =-\displaystyle \frac{5}{{13}}\\\cos 2\theta & =2{{\cos }^{2}}\theta -1\\&=2{{\left( {-\displaystyle \frac{5}{{13}}} \right)}^{2}}-1\\&=2\left( {\displaystyle \frac{{25}}{{169}}} \right)-1\\&=\displaystyle \frac{{50}}{{169}}-1\\&=\displaystyle \frac{{50-169}}{{169}}\\&=-\displaystyle \frac{{119}}{{169}}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\sin 2\theta &=2\sin \theta \cos \theta \\&=2\times \left( {-\displaystyle \frac{{12}}{{13}}\times -\displaystyle \frac{5}{{13}}} \right)\\&=2\times \left( {\displaystyle \frac{{60}}{{169}}} \right)\\&=\displaystyle \frac{{120}}{{169}}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\tan 2\theta &=\displaystyle \frac{{\sin 2\theta }}{{\cos 2\theta }}\\&=\displaystyle \frac{{\displaystyle \frac{{120}}{{169}}}}{{-\displaystyle \frac{{119}}{{169}}}}\\&=-\displaystyle \frac{{120}}{{169}}\times \displaystyle \frac{{169}}{{119}}\\&=-\displaystyle \frac{{120}}{{119}}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\sin ({{180}^\circ}-2\theta )&=\sin 2\theta \\&=\displaystyle \frac{{120}}{{169}}\end{align*}[/latex]
- .
Unit 1: Assessment
- .
[latex]\scriptsize \displaystyle \begin{align*}\text{LHS}&=\sin {{75}^\circ}+\sin {{15}^\circ}\\&=\sin ({{45}^\circ}+{{30}^\circ})+\sin ({{45}^\circ}-{{30}^\circ})\\&=\sin {{45}^\circ}\cos {{30}^\circ}+\cos {{45}^\circ}\sin {{30}^\circ}+\sin {{45}^\circ}\cos {{30}^\circ}-\cos {{45}^\circ}\sin {{30}^\circ}\\&=2\sin {{45}^\circ}\cos {{30}^\circ}\\&=2\times \displaystyle \frac{1}{{\sqrt{2}}}\times \displaystyle \frac{{\sqrt{3}}}{2}\\&=\displaystyle \frac{{\sqrt{3}}}{{\sqrt{2}}}\\&=\displaystyle \frac{{\sqrt{6}}}{2}=\text{RHS}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}\text{LHS}&=\displaystyle \frac{{\sin 2\theta }}{{\sin \theta }}-\displaystyle \frac{{\cos 2\theta }}{{\cos \theta }}\\&=\displaystyle \frac{{2\sin \theta \cos \theta }}{{\sin \theta }}-\displaystyle \frac{{2{{{\cos }}^{2}}\theta -1}}{{\cos \theta }}\\&=\displaystyle \frac{{2\sin \theta {{{\cos }}^{2}}\theta -2\sin \theta {{{\cos }}^{2}}\theta +\sin \theta }}{{\sin \theta \cos \theta }}\\&=\displaystyle \frac{{\sin \theta }}{{\sin \theta \cos \theta }}\\&=\displaystyle \frac{1}{{\cos \theta }}=\text{RHS}\end{align*}[/latex]. - [latex]\scriptsize \cos \theta =a[/latex]
[latex]\scriptsize \begin{align*}\cos 3\theta &=\cos (\theta +2\theta )\\&=\cos \theta \cos 2\theta -\sin \theta \sin 2\theta \\&=\cos \theta \left( {2{{{\cos }}^{2}}\theta -1} \right)-\sin \theta \left( {2\sin \theta \cos \theta } \right)\\&=2{{\cos }^{3}}\theta -\cos \theta -2{{\sin }^{2}}\theta \cos \theta \\&=\cos \theta \left( {2{{{\cos }}^{2}}\theta -1-2{{{\sin }}^{2}}\theta } \right)\\&=\cos \theta \left( {2{{{\cos }}^{2}}\theta -1-2(1-{{{\cos }}^{2}}\theta )} \right)\\&=\cos \theta \left( {2{{{\cos }}^{2}}\theta -1-2+2{{{\cos }}^{2}}\theta } \right)\\&=\cos \theta \left( {4{{{\cos }}^{2}}\theta -3} \right)\\&=a(4{{a}^{2}}-3)\end{align*}[/latex] - .
- .
[latex]\scriptsize \begin{align*}\text{LHS}&=\sin (S+T)-\sin (S-T)\\&=\sin S\cos T+\cos S\sin T-\left( {\sin S\cos T-\cos S\sin T} \right)\\&=\sin S\cos T+\cos S\sin T-\sin S\cos T+\cos S\sin T\\&=2\cos S\sin T=\text{RHS}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}2\cos S\sin T & =\sin (S+T)-\sin (S-T)\\\therefore \cos S\sin T & =\displaystyle \frac{1}{2}\left( {\sin (S+T)-\sin (S-T)} \right)\\\text{Let }S={{15}^\circ}\text{ } & \text{and }T={{75}^\circ}\\\therefore \cos {{15}^\circ}\sin {{75}^\circ} & =\displaystyle \frac{1}{2}\left( {\sin ({{{15}}^\circ}+{{{75}}^\circ})-\sin ({{{15}}^\circ}-{{{75}}^\circ})} \right)\\&=\displaystyle \frac{1}{2}\left( {\sin {{{90}}^\circ}-\sin (-{{{60}}^\circ})} \right)\\&=\displaystyle \frac{1}{2}\left( {1+\sin {{{60}}^\circ}} \right)\\&=\displaystyle \frac{1}{2}\left( {1+\displaystyle \frac{{\sqrt{3}}}{2}} \right)\\&=\displaystyle \frac{1}{2}\left( {\displaystyle \frac{{2+\sqrt{3}}}{2}} \right)\\&=\displaystyle \frac{{2+\sqrt{3}}}{4}\end{align*}[/latex]
- .
- .
- .
[latex]\scriptsize \begin{align*}\text{LHS}&=\tan 2x+\displaystyle \frac{1}{{\cos 2x}}\\&=\displaystyle \frac{{\sin 2x}}{{\cos 2x}}+\displaystyle \frac{1}{{\cos 2x}}\\&=\displaystyle \frac{{\sin 2x+1}}{{\cos 2x}}\\&=\displaystyle \frac{{2\sin x\cos x+1}}{{{{{\cos }}^{2}}x-{{{\sin }}^{2}}x}}\quad \quad \text{ but }{{\sin }^{2}}x+{{\cos }^{2}}x=1\text{ so}\\&=\displaystyle \frac{{2\sin x\cos x+{{{\sin }}^{2}}x+{{{\cos }}^{2}}x}}{{\left( {\cos x+\sin x} \right)\left( {\cos x-\sin x} \right)}}\\&=\displaystyle \frac{{{{{\cos }}^{2}}x+2\sin x\cos x+{{{\sin }}^{2}}x}}{{\left( {\cos x+\sin x} \right)\left( {\cos x-\sin x} \right)}}\\&=\displaystyle \frac{{(\cos x+\sin x)(\cos x+\sin x)}}{{\left( {\cos x+\sin x} \right)\left( {\cos x-\sin x} \right)}}\\&=\displaystyle \frac{{\sin x+\cos x}}{{\cos x-\sin x}}=\text{RHS}\end{align*}[/latex]. - When [latex]\scriptsize x={{45}^\circ}[/latex], [latex]\scriptsize \cos x=\sin x[/latex]. Therefore, [latex]\scriptsize \cos x-\sin x=0[/latex].
- .
- .
[latex]\scriptsize \begin{align*}\cos {{135}^\circ} & =\cos ({{67.5}^\circ}+{{67.5}^\circ})\\=2{{\cos }^{2}}{{67.5}^\circ}-1\\\text{But }\cos {{135}^\circ} & =\cos ({{180}^\circ}-{{45}^\circ})\\&=-\cos {{45}^\circ}\\&=-\displaystyle \frac{1}{{\sqrt{2}}}\\\therefore 2{{\cos }^{2}}{{67.5}^\circ}-1 & =-\displaystyle \frac{1}{{\sqrt{2}}}\\\therefore 2{{\cos }^{2}}{{67.5}^\circ} & =1-\displaystyle \frac{1}{{\sqrt{2}}}=\displaystyle \frac{{\sqrt{2}-1}}{{\sqrt{2}}}\\\therefore {{\cos }^{2}}{{67.5}^\circ} & =\displaystyle \frac{{\sqrt{2}-1}}{{2\sqrt{2}}}\\\therefore \cos {{67.5}^\circ} & =\sqrt{{\displaystyle \frac{{\sqrt{2}-1}}{{2\sqrt{2}}}}}\\&=\sqrt{{\displaystyle \frac{{2-\sqrt{2}}}{4}}}\\&=\displaystyle \frac{{\sqrt{{2-\sqrt{2}}}}}{2}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\text{LHS}&=\sin (A+B)\times \sin (A-B)\\&=\left( {\sin A\cos B+\cos A\sin B} \right)\times \left( {\sin A\cos B-\cos A\sin B} \right)\quad \quad \text{Difference of two squares}\\&={{\left( {\sin A\cos B} \right)}^{2}}-{{\left( {\cos A\sin B} \right)}^{2}}\\&={{\sin }^{2}}A{{\cos }^{2}}B-{{\cos }^{2}}A{{\sin }^{2}}B\\&={{\sin }^{2}}A(1-{{\sin }^{2}}B)-(1-{{\sin }^{2}}A){{\sin }^{2}}B\\&={{\sin }^{2}}A-{{\sin }^{2}}A{{\sin }^{2}}B-{{\sin }^{2}}B+{{\sin }^{2}}A{{\sin }^{2}}B\\&={{\sin }^{2}}A-{{\sin }^{2}}B=\text{RHS}\end{align*}[/latex] - [latex]\scriptsize {{90}^\circ} \lt A \lt {{360}^\circ}[/latex] and [latex]\scriptsize \tan A=\displaystyle \frac{3}{2}[/latex]
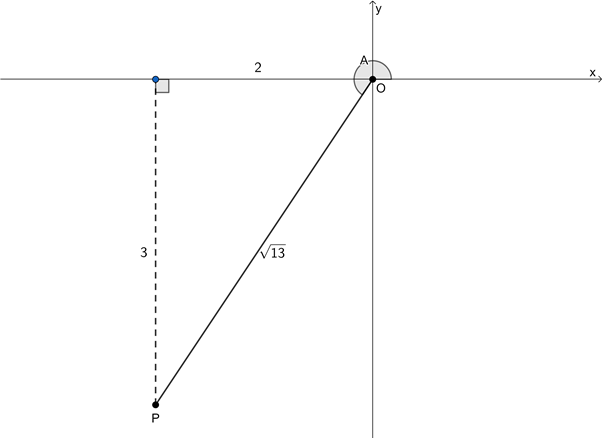
[latex]\scriptsize \begin{align*}\text{LHS}&=\cos 2A-\sin 2A\\&=2{{\cos }^{2}}A-1-\left( {2\sin A\cos A} \right)\\&=2{{\left( {-\displaystyle \frac{2}{{\sqrt{{13}}}}} \right)}^{2}}-1-2\left( {-\displaystyle \frac{3}{{\sqrt{{13}}}}} \right)\left( {-\displaystyle \frac{2}{{\sqrt{{13}}}}} \right)\\&=2\left( {\displaystyle \frac{4}{{13}}} \right)-1-2\left( {\displaystyle \frac{6}{{13}}} \right)\\&=\displaystyle \frac{8}{{13}}-1-\displaystyle \frac{{12}}{{13}}\\&=\displaystyle \frac{{8-13-12}}{{13}}\\&=-\displaystyle \frac{{17}}{{13}}=\text{RHS}\end{align*}[/latex]. - .
[latex]\scriptsize \begin{align*}\text{LHS}&=\cos (A+B)-\cos (A-B)\\&=\cos A\cos B-\sin A\sin B-\left( {\cos A\cos B+\sin A\sin B} \right)\\&=\cos A\cos B-\sin A\sin B-\cos A\cos B-\sin A\sin B\\&=-2\sin A\sin B=\text{RHS}\end{align*}[/latex].
Media Attributions
- activity1.1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example1.3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.2 A3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment A8 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license