Functions and algebra: Use a variety of techniques to sketch and interpret information for graphs of the inverse of a function
Unit 1: Determine and sketch the inverse of a linear function
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Define an inverse function.
- Find the inverse of [latex]\scriptsize y=ax+q[/latex].
- Sketch the inverse of [latex]\scriptsize y=ax+q[/latex].
- Answer questions about the domain, range, shape, continuity and other characteristics of the inverse graph.
What you should know
Before you start this unit, make sure you can:
- Define a relation and a function. Refer to level 2 subject outcome 2.1 unit 1 if you need help with this.
- Sketch linear functions using the dual-intercept method. Refer to level 2 subject outcome 2.1 unit 1 if you need help with this.
Introduction
In levels 2 and 3 we learnt about the following functions:
- Linear functions
- [latex]\scriptsize y=ax+q[/latex]
- [latex]\scriptsize y=mx+c[/latex]
- Quadratic functions
- [latex]\scriptsize y=a{{x}^{2}}+q[/latex]
- [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex]
- [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex]
- Exponential function
- [latex]\scriptsize y=a\cdot {{b}^{{x+p}}}+q,b \gt 0,b\ne 1[/latex]
- Hyperbolic function
- [latex]\scriptsize y=\displaystyle \frac{a}{{x+p}}+q[/latex]
- Trigonometric functions
- [latex]\scriptsize y=a\sin (x+p)+q[/latex]
- [latex]\scriptsize y=a\sin kx[/latex]
- [latex]\scriptsize y=a\cos (x+p)+q[/latex]
- [latex]\scriptsize y=a\cos kx[/latex]
- [latex]\scriptsize y=a\tan (x+p)+q[/latex]
- [latex]\scriptsize y=a\tan kx[/latex]
We learnt about the characteristics of each function, how to sketch their graphs and how the values of [latex]\scriptsize a,p,q,b[/latex] and [latex]\scriptsize k[/latex] affect the shape and position of these graphs. We also learnt how to find the equations of these functions based on their graphs.
The important thing to note is that they were all functions.
Function revision
Relations are mathematical rules (equations) that associate each element of one set of numbers with at least one element of another set of numbers. We can think of the first set of numbers as the input (or independent variables) and the second set of numbers the output (or the dependent variables). We put an input number into the relation rule or equation and get at least one output number. The value of the output depends on the value of the input.
Functions are special types of relations. They are rules that associate each element of the input set with only one element of the output set. Therefore, when we put an input number into the function rule or equation, we only ever get one output number. Every function is a relation but not every relation is a function (see Figure 1).
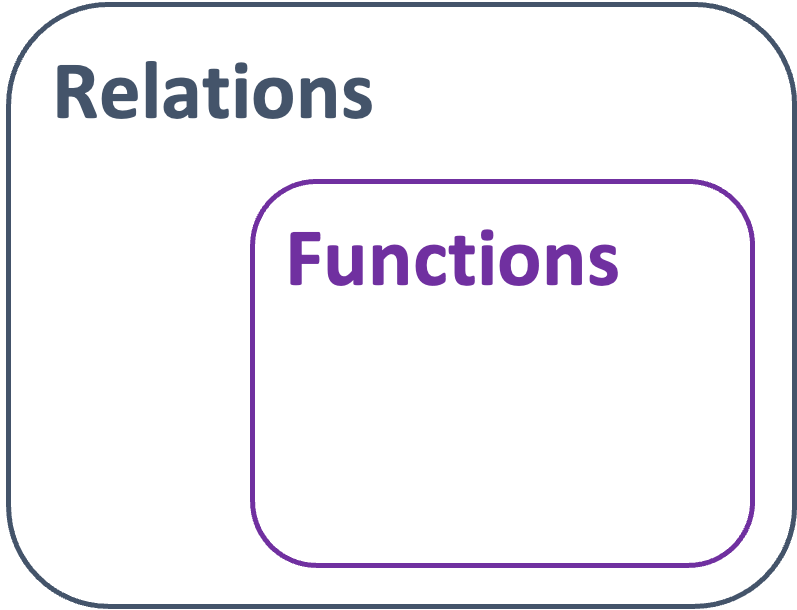
We call the set of input numbers or independent variables the domain. We call the set of output numbers or dependent variables the range.
Relation:
A mathematical rule that associates each element of a set [latex]\scriptsize (A)[/latex] with at least one element in another set [latex]\scriptsize (B)[/latex].
Function:
A mathematical rule that uniquely associates elements of one set [latex]\scriptsize (A)[/latex] with the elements of another set [latex]\scriptsize (B)[/latex] such that each element in a set [latex]\scriptsize (A)[/latex] maps to only one element in the other set [latex]\scriptsize (B)[/latex].
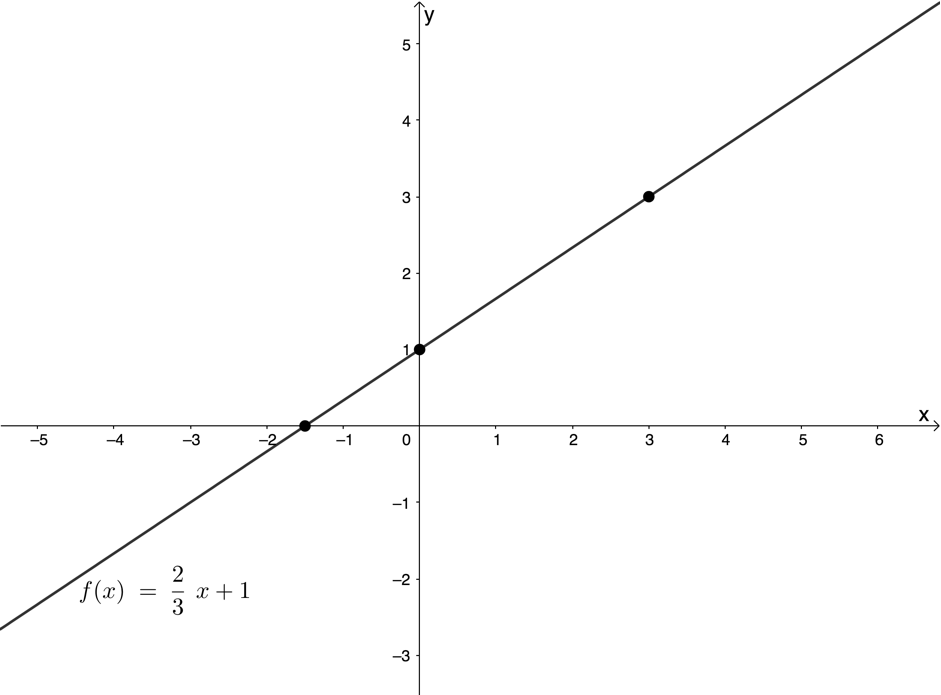
Some functions are one-to-one functions (see Figure 2). In one-to-one functions, each element of the input set is uniquely associated with an output. In other words, each output is produced by only one input.
The linear function is an example of a one-to-one function. Each output value or y-value is produced by only one input value or x-value (see Figure 3).
Some functions are many-to-one functions (see Figure 4). In many-to-one functions, each element of the input set is associated with an output but not uniquely. In other words, an output can be produced by more than one input.
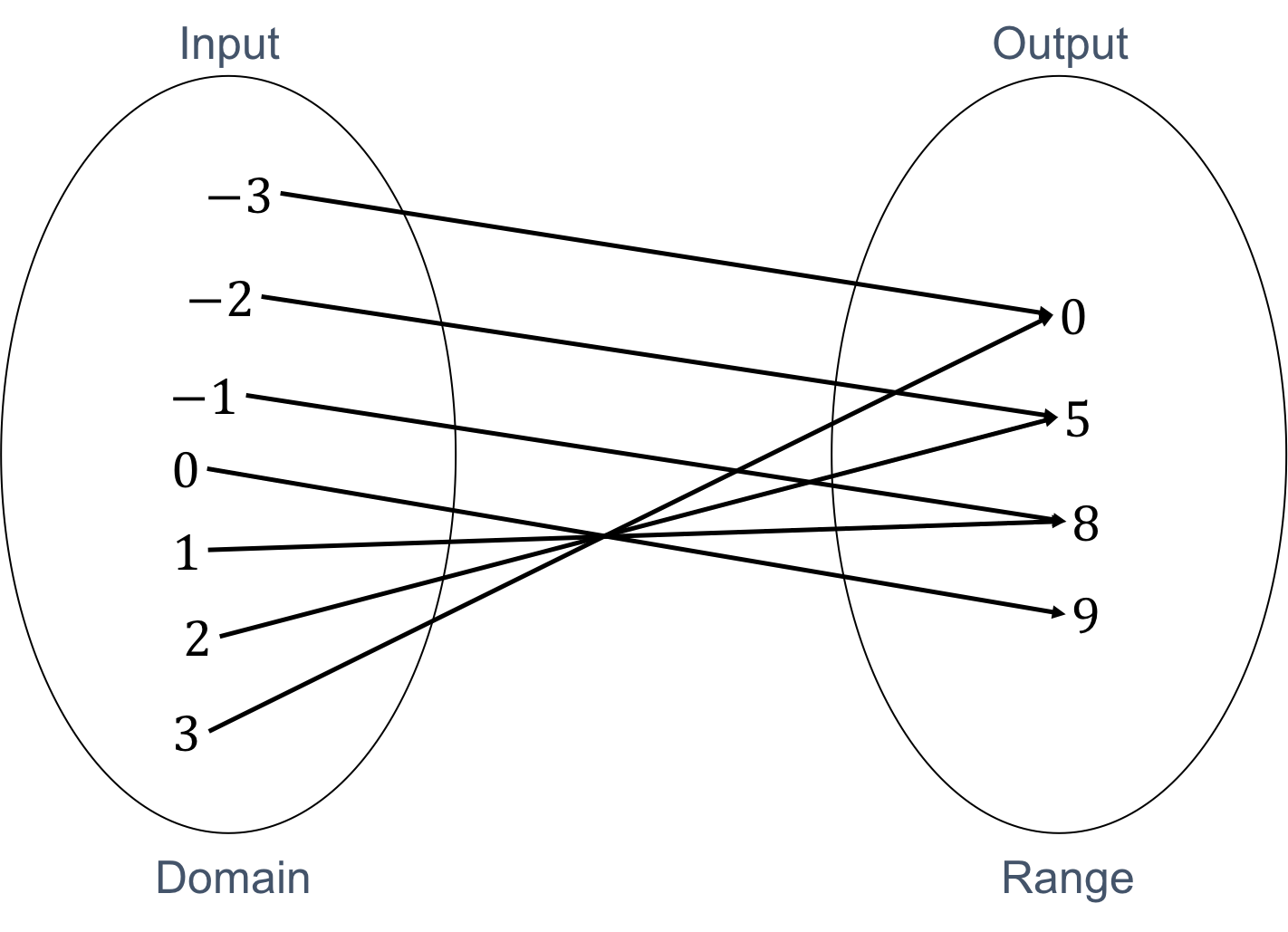
The quadratic function is an example of a many-to-one function. Each output value or y-value is produced by two input values or x-values (see Figure 5).
The vertical line test
Because we know that for a relation to be a function each element of the input set must be associated with only one element of the output set, we can use a simple visual test to see if a graph is the graph of a function or not. This is the vertical line test.
If we can place a vertical line over the graph and have it cut the graph more than once, then we know that there is an input value which produces more than one output value and so the graph is not the graph of a function.
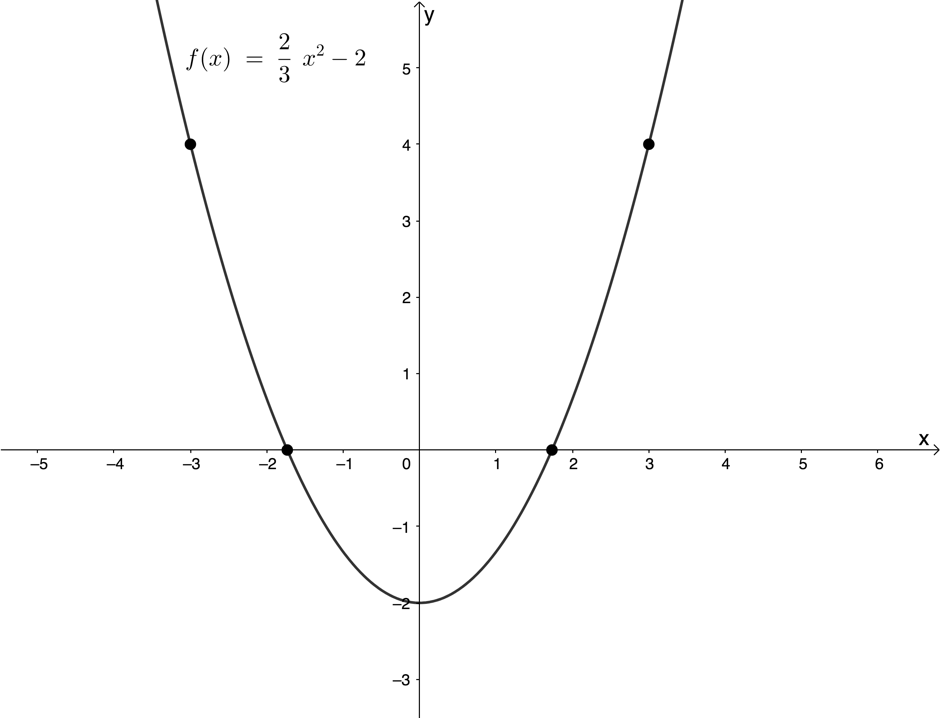
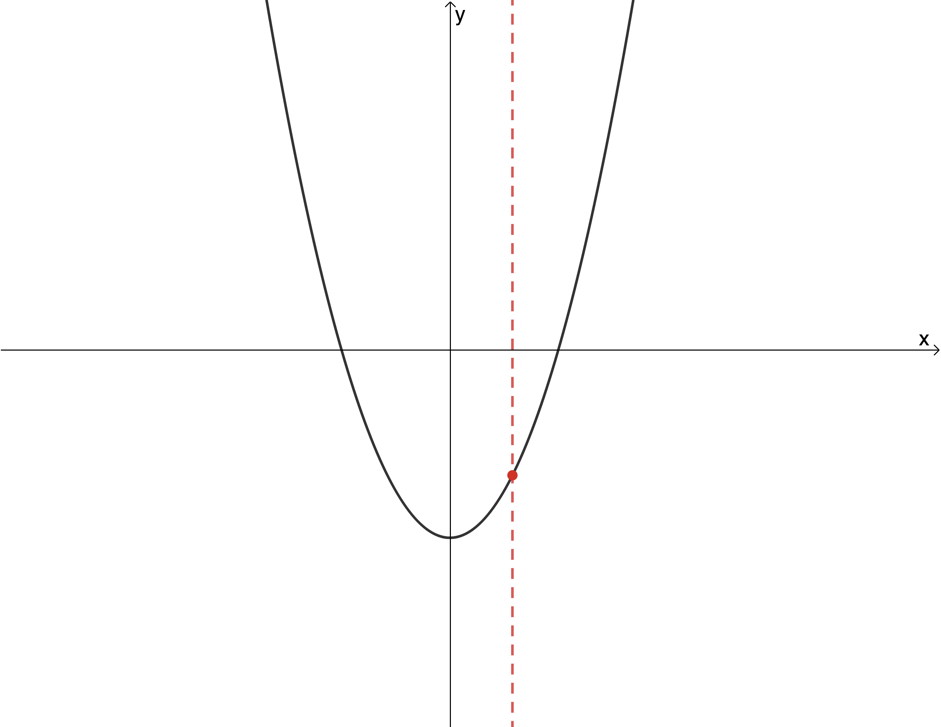
Figure 6 uses the vertical line test to confirm that [latex]\scriptsize y=\displaystyle \frac{2}{3}{{x}^{2}}-2[/latex] is a function. At no point is any input value associated with more than one output value.
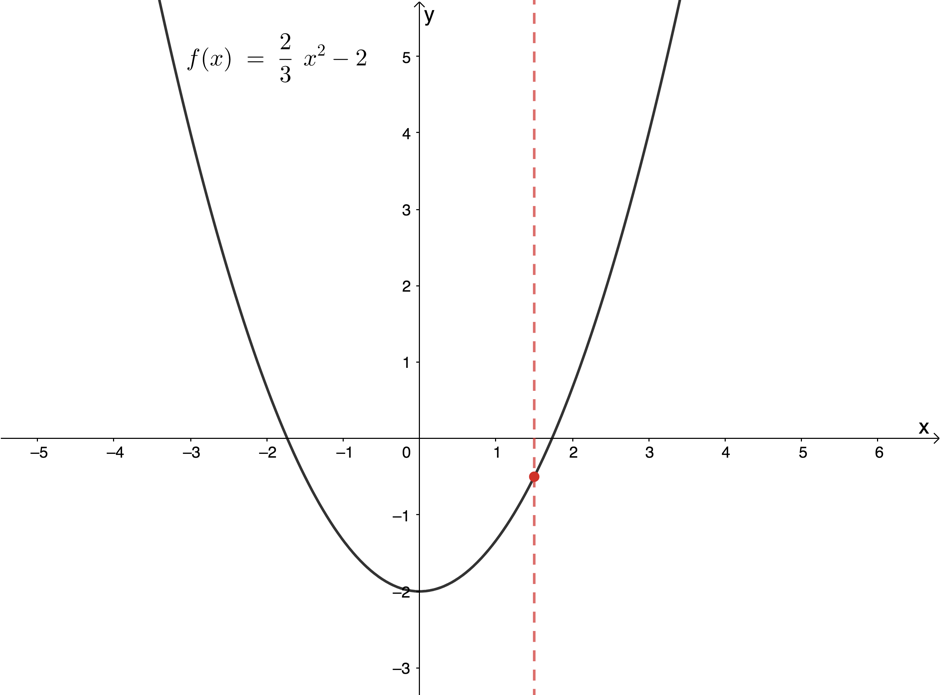
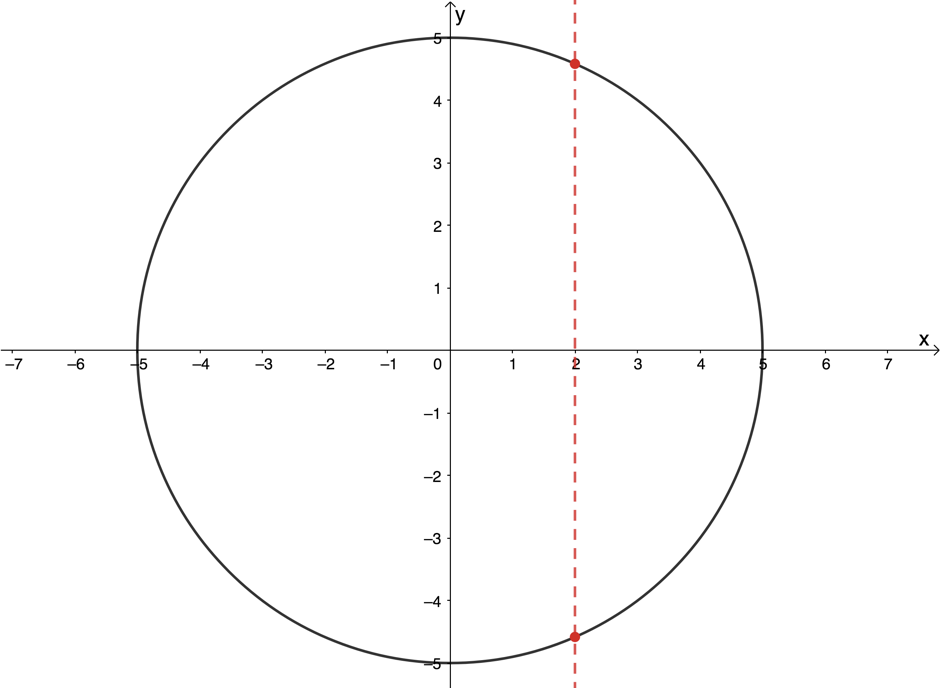
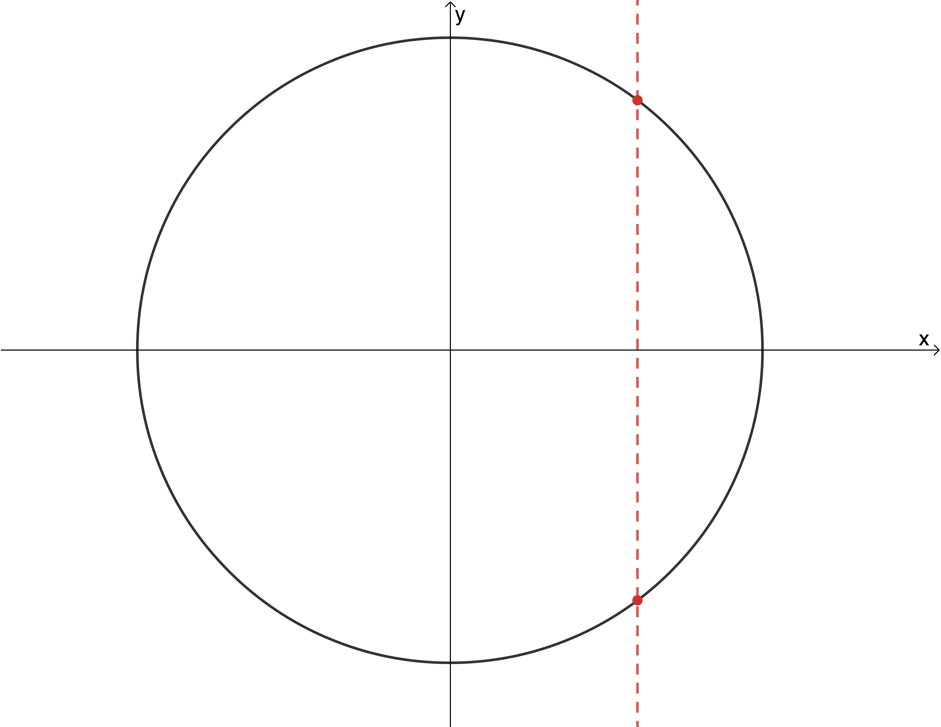
Figure 7 shows that [latex]\scriptsize y=\pm \sqrt{{25-{{x}^{2}}}}[/latex] is not a function. We can see that at least one input value is associated with more than one output value. In fact, almost all the input values are associated with more than one output value.
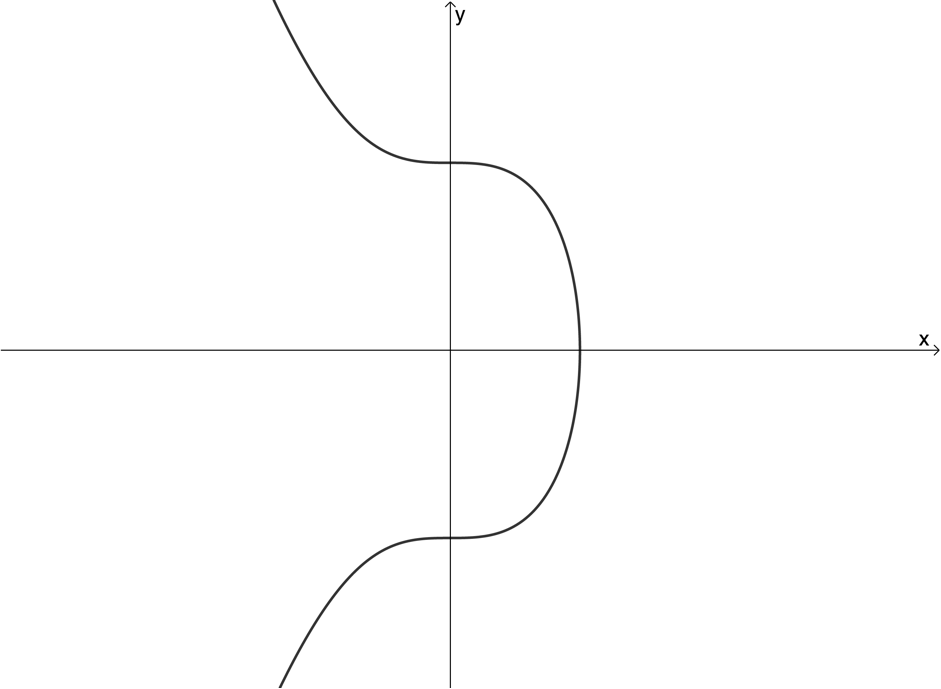
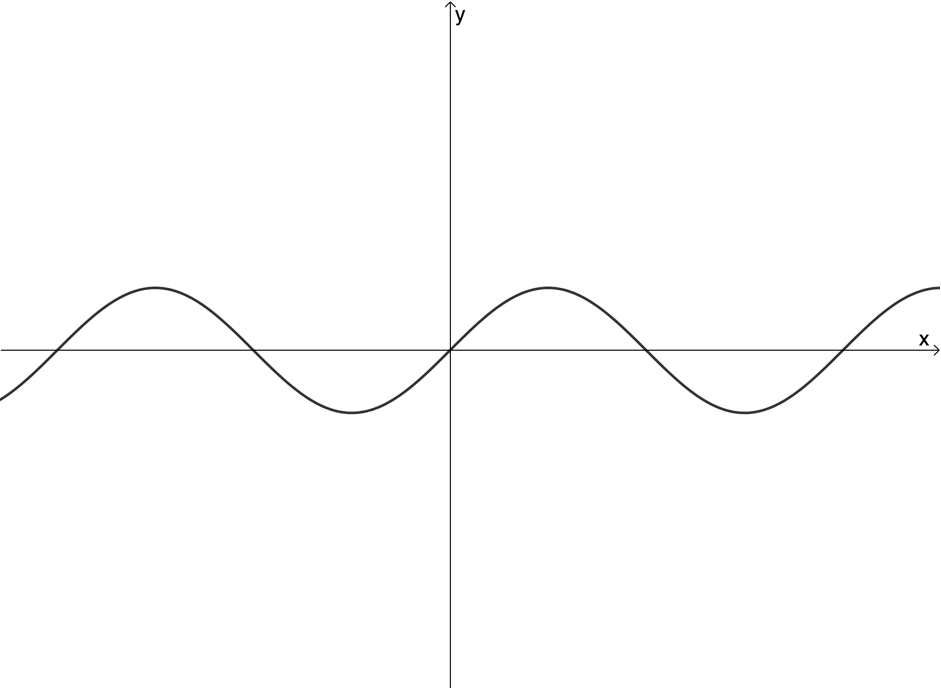
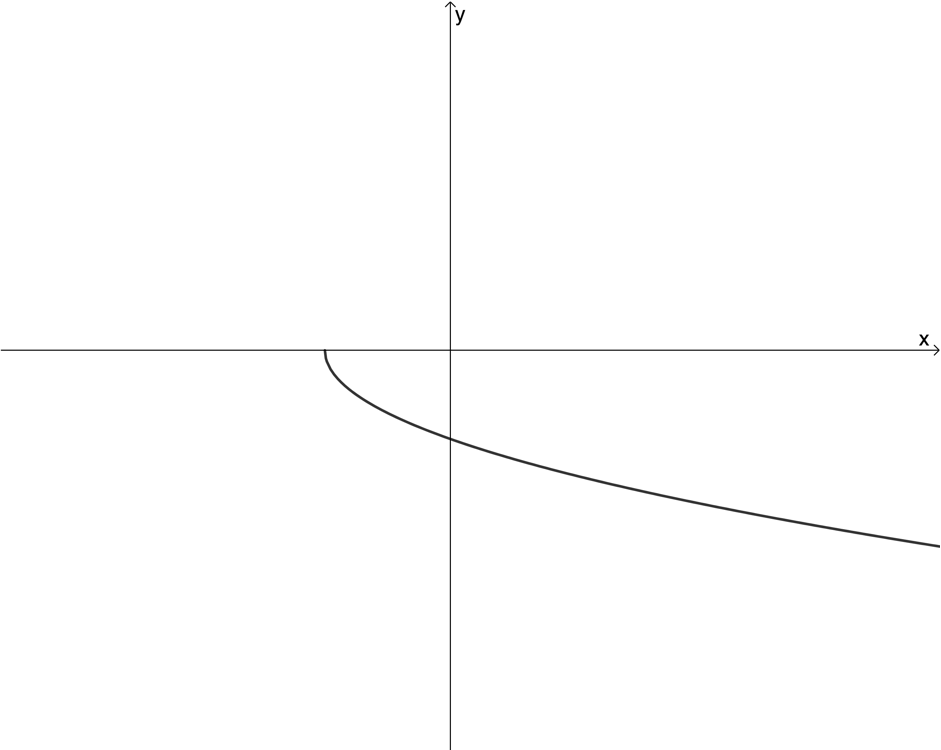
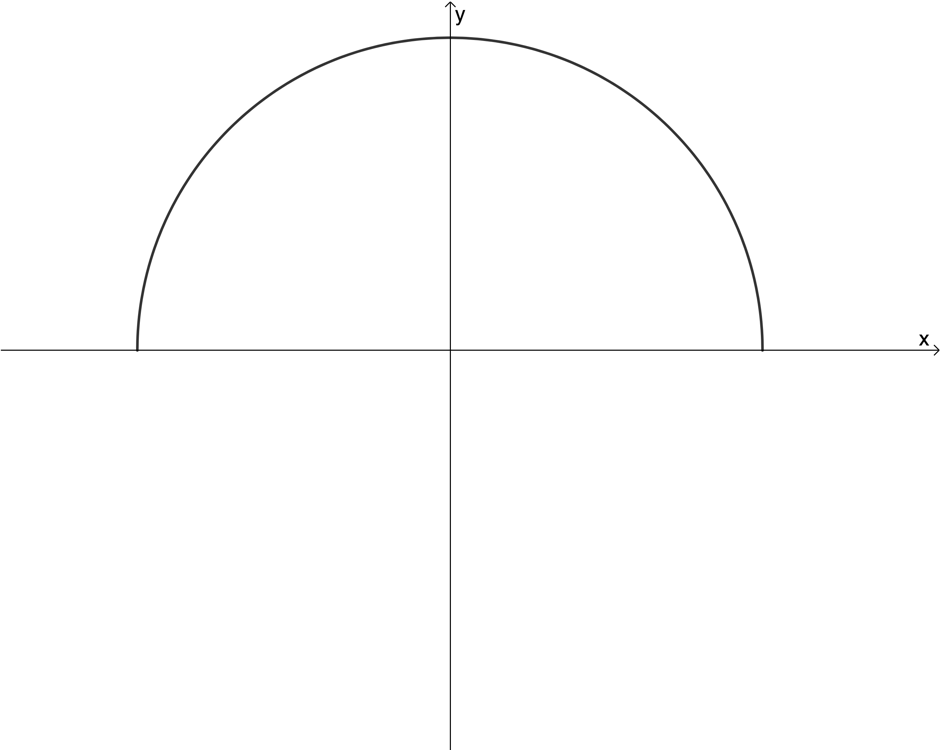
Exercise 1.1
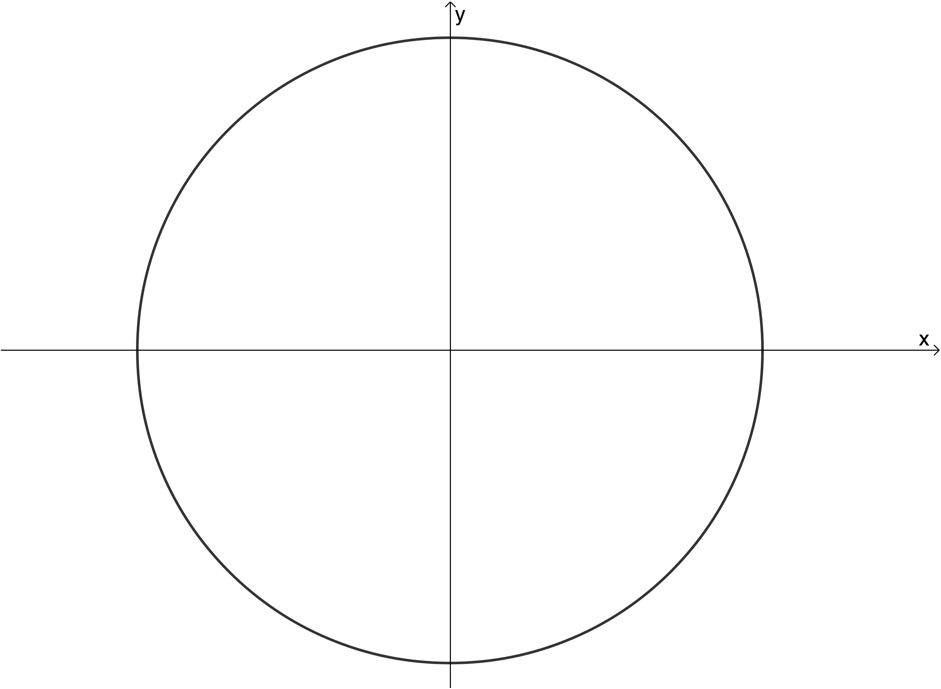
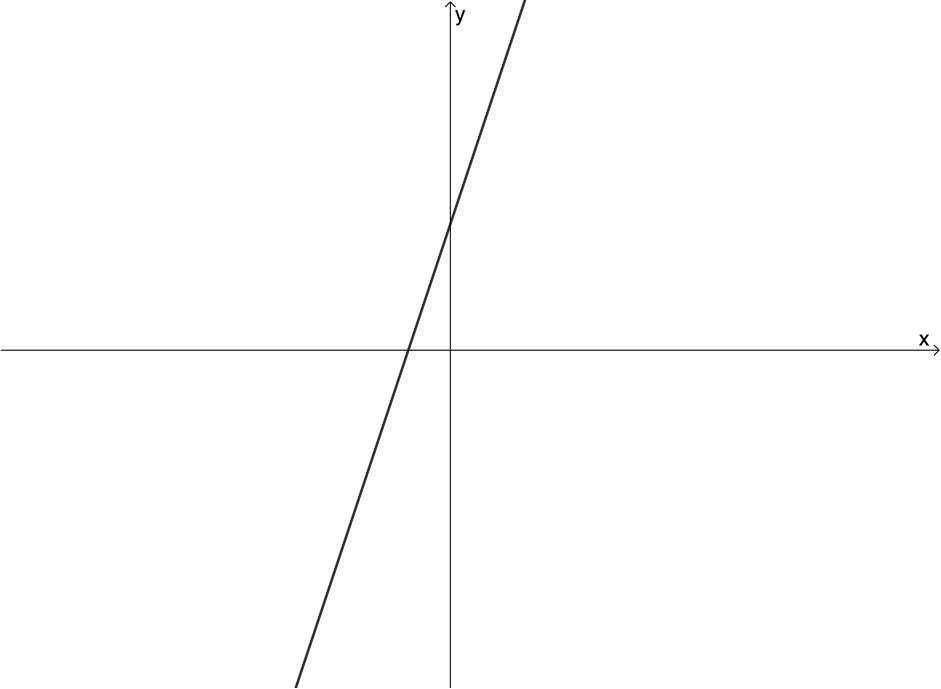
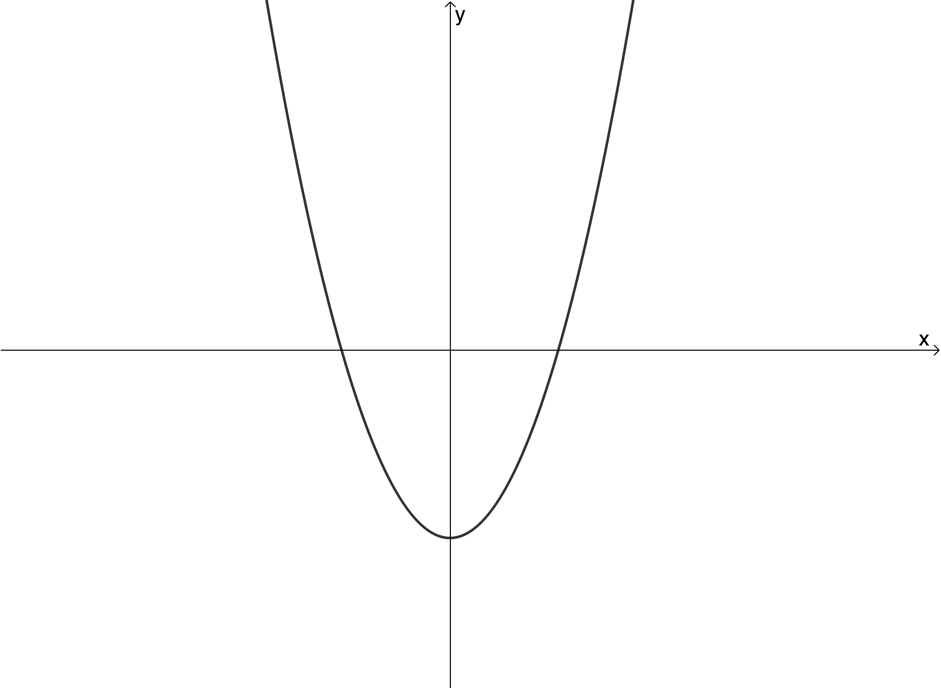
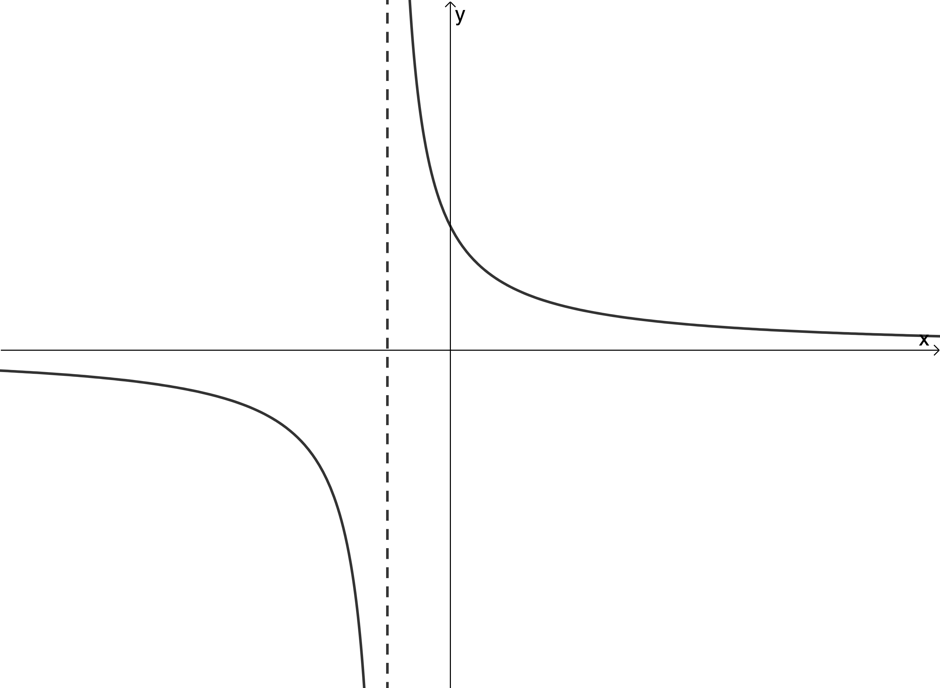
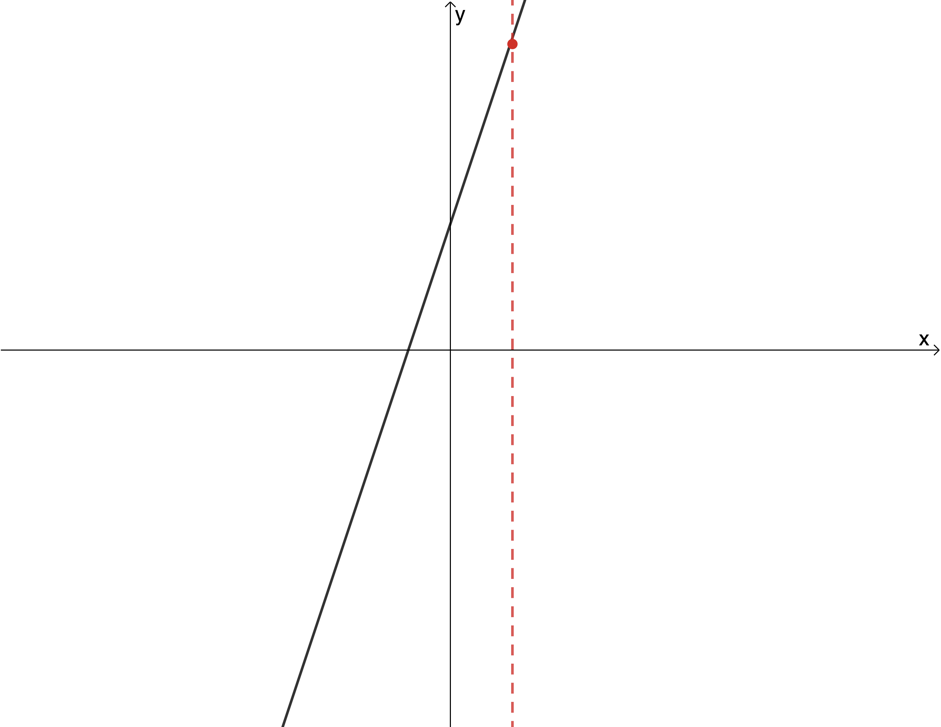
Use the vertical line test to determine whether the following graphs are graphs of functions or not:
The full solutions are at the end of the unit.
Function notation
We know that we can use a special notation to represent functions, called function notation. For example, in [latex]\scriptsize h(s)=3s+2[/latex] the function is called [latex]\scriptsize h[/latex] and the independent variable is [latex]\scriptsize s[/latex]. We say that ‘h of s is equal to three s plus two’.
[latex]\scriptsize h(2)[/latex] (h of two) means the function value (or the output value) when the input value is two. Therefore [latex]\scriptsize h(2)=3(2)+2=8[/latex].
If [latex]\scriptsize h(s)=1[/latex] then [latex]\scriptsize 3s+2=1[/latex]. Therefore, [latex]\scriptsize s=-\displaystyle \frac{1}{3}[/latex].
Unless a relation is a function, we may not represent it using function notation. From Figure 7, we know that [latex]\scriptsize y=\pm \sqrt{{25-{{x}^{2}}}}[/latex] is not a function. Therefore, we cannot represent this relation using function notation as [latex]\scriptsize f(x)=\pm \sqrt{{25-{{x}^{2}}}}[/latex].
However, we can say that [latex]\scriptsize f(x)=+\sqrt{{25-{{x}^{2}}}}[/latex] (see Figure 8) or that [latex]\scriptsize f(x)=-\sqrt{{25-{{x}^{2}}}}[/latex] (see Figure 9) because, once we restrict the output to being either the positive or negative root, the relation is a function.
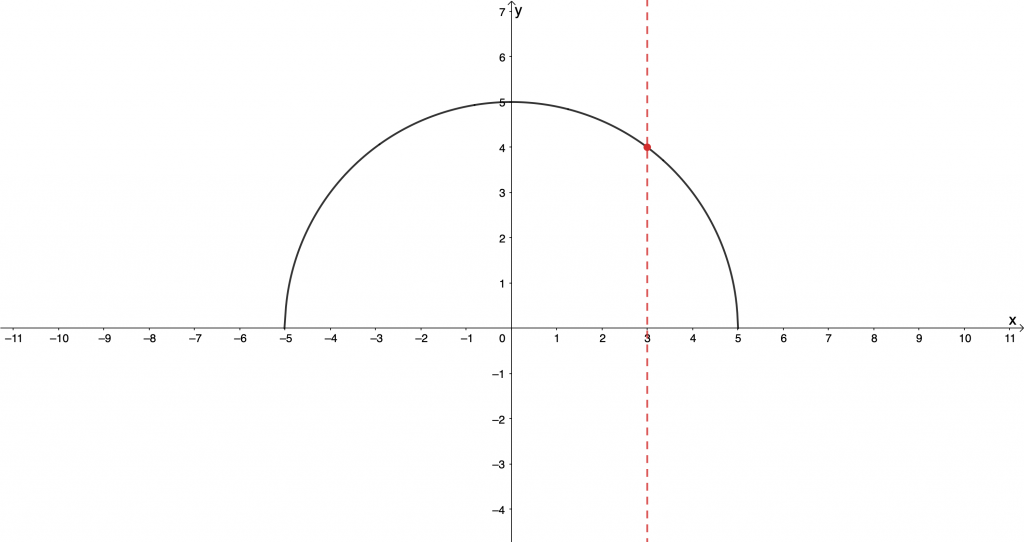
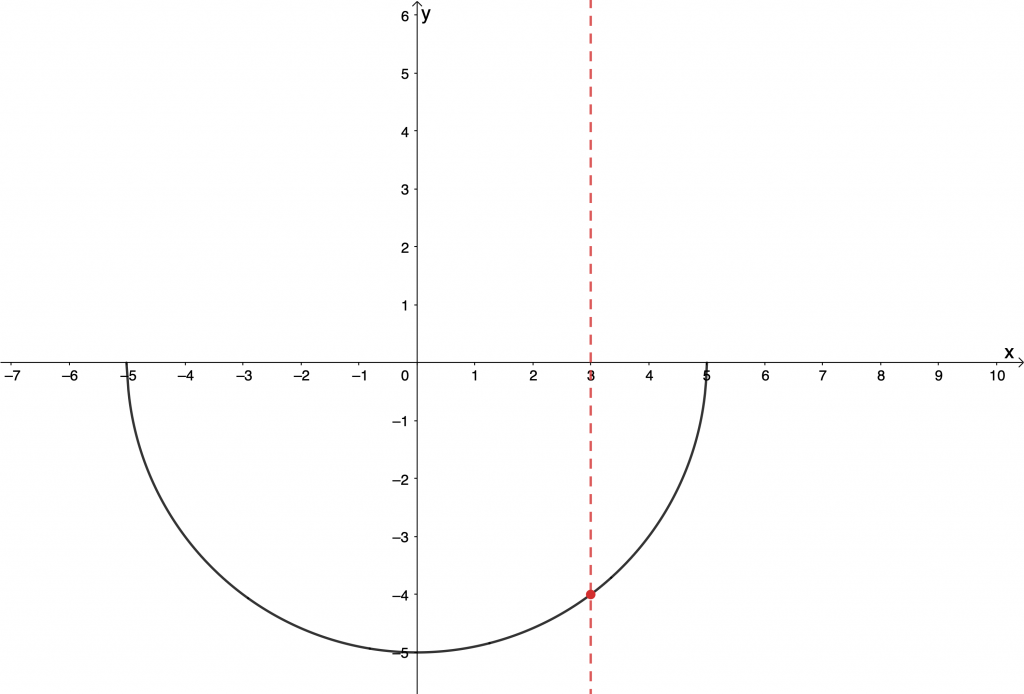
Inverse functions
If we have the function [latex]\scriptsize f(x)=4x-5[/latex], then we know that if we put [latex]\scriptsize x=2[/latex] into the function, we will get the output of [latex]\scriptsize y=3[/latex].
The inverse of a function does the ‘reverse’ of a given function. The inverse of the function [latex]\scriptsize f[/latex] will, therefore, take the input of [latex]\scriptsize x=3[/latex] and produce the output of [latex]\scriptsize y=2[/latex].
If a function is a one-to-one function, then its inverse will also be a function and we can represent the inverse using inverse function notation. If the function is [latex]\scriptsize f(x)[/latex], then the inverse function is denoted as [latex]\scriptsize {{f}^{{-1}}}(x)[/latex]. Note that the [latex]\scriptsize -1[/latex] does not represent an exponent.
We say that functions whose inverses are also functions are invertible.
To find the inverse of a function, we simply need to swop the [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex] in the original function equation. If [latex]\scriptsize f(x)=4x-5[/latex] then we know that [latex]\scriptsize y=4x-5[/latex]. Therefore, the inverse of [latex]\scriptsize f[/latex] is [latex]\scriptsize x=4y-5[/latex].
We then need to rearrange the inverse equation into the [latex]\scriptsize y=[/latex] form.
[latex]\scriptsize \begin{align*}x & =4y-5\\\therefore 4y & =x+5\\\therefore y & =\displaystyle \frac{1}{4}x+\displaystyle \frac{5}{4}\end{align*}[/latex]
So, if [latex]\scriptsize f(x)=4x-5[/latex] then we can say that [latex]\scriptsize {{f}^{{-1}}}(x) =\displaystyle \frac{1}{4}x+\displaystyle \frac{5}{4}[/latex]. Remember that we can only use the inverse function notation because [latex]\scriptsize f[/latex] is a one-to-one function and, therefore, [latex]\scriptsize {{f}^{{-1}}}(x)[/latex] is also a function.
If we saw that [latex]\scriptsize f(2)=3[/latex], check to make sure that [latex]\scriptsize {{f}^{{-1}}}(3)=2[/latex].
Take note!
If the inverse of a function is also a function, that function is said to be invertible. Only one-to-one functions are invertible.
Often, however, the inverse of a function is not a function. Let’s look at the following example.
Example 1.1
Find the inverse of [latex]\scriptsize g(x)=2{{x}^{2}}-8[/latex] and state whether it is a function or not.
Solution
We start by writing the given function in [latex]\scriptsize y=[/latex] form.
[latex]\scriptsize \begin{align*}g(x) & =2{{x}^{2}}-8\\\therefore y & =2{{x}^{2}}-8\end{align*}[/latex]
To find the inverse, we interchange the [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex] in the original function equation and get the new equation into [latex]\scriptsize y=[/latex] form.
[latex]\scriptsize \begin{align*}x & =2{{y}^{2}}-8\\\therefore 2{{y}^{2}} & =x+8\\\therefore {{y}^{2}} & =\displaystyle \frac{x}{2}+4\\\therefore y & =\pm \sqrt{{\displaystyle \frac{x}{2}+4}}\end{align*}[/latex]
We can see that for every input we put into the inverse of [latex]\scriptsize g[/latex] we will get two outputs. Therefore, the inverse of [latex]\scriptsize g[/latex] is not a function and we cannot write it using inverse function notation.
Take note!
Do not confuse inverse function notation with the reciprocal of a function.
If [latex]\scriptsize f(x)=2x[/latex] then:
- the inverse of [latex]\scriptsize f[/latex] is [latex]\scriptsize {{f}^{{-1}}}(x)=\displaystyle \frac{1}{2}x[/latex]
- the reciprocal of [latex]\scriptsize f[/latex] is [latex]\scriptsize {{\left[ {f(x)} \right]}^{{-1}}}=\displaystyle \frac{1}{{f(x)}}=\displaystyle \frac{1}{{2x}}[/latex]
The inverse of the linear function
Because linear functions are one-to-one functions, we know that their inverses will also be functions. Therefore, linear functions are invertible.
Example 1.2
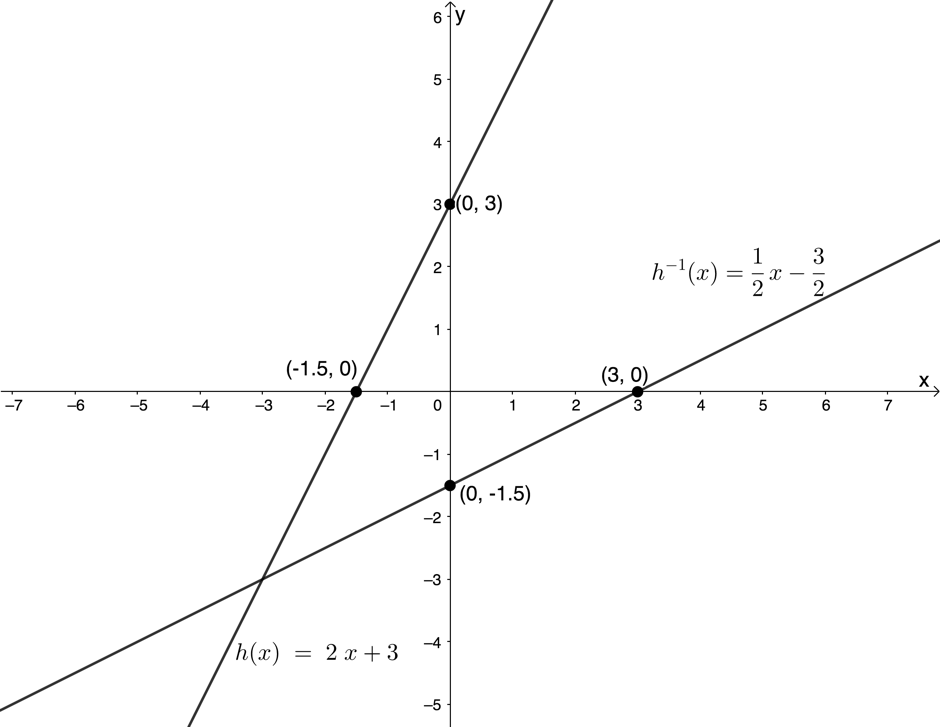
Given [latex]\scriptsize h(x)=-2x+3[/latex]:
- Determine [latex]\scriptsize {{h}^{{-1}}}(x)[/latex].
- Sketch [latex]\scriptsize h(x)[/latex] and [latex]\scriptsize {{h}^{{-1}}}(x)[/latex] on the same set of axes, showing the intercepts with the axes.
- State the domain and range of [latex]\scriptsize h(x)[/latex] and [latex]\scriptsize {{h}^{{-1}}}(x)[/latex].
- About what line are the graphs of [latex]\scriptsize h(x)[/latex] and [latex]\scriptsize {{h}^{{-1}}}(x)[/latex] symmetrical?
Solutions
- Step 1: Start by writing the original function in [latex]\scriptsize y=[/latex] form.
[latex]\scriptsize y=-2x+3[/latex]
.
Step 2: Interchange [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex] and write the inverse equation in [latex]\scriptsize y=[/latex] form.
[latex]\scriptsize \begin{align*}x & =-2y+3\\\therefore 2y & =-x+3\\\therefore y & =-\displaystyle \frac{1}{2}x+\displaystyle \frac{3}{2}\end{align*}[/latex]
.
Step 3: Write the inverse using inverse function notation if it is also a function.
[latex]\scriptsize {{h}^{{-1}}}(x)=-\displaystyle \frac{1}{2}x+\displaystyle \frac{3}{2}[/latex] - Here are the sketches of [latex]\scriptsize h(x)[/latex] and [latex]\scriptsize {{h}^{{-1}}}(x)[/latex].
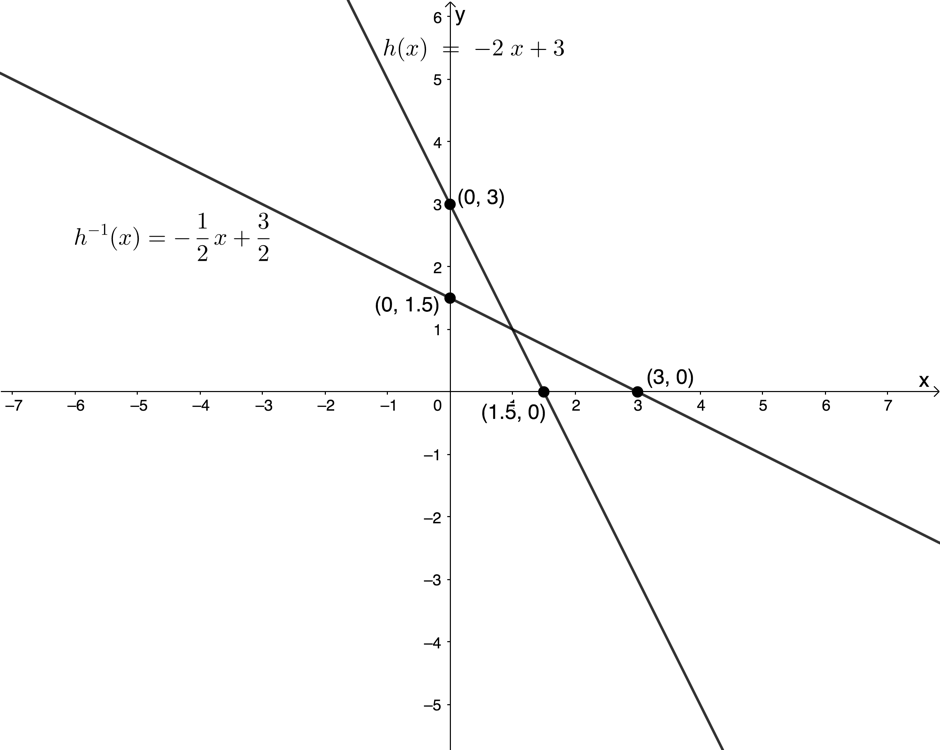
- Domain of [latex]\scriptsize h(x)[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R}\}\text{ }[/latex]
Range of [latex]\scriptsize h(x)[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R}\}\text{ }[/latex]
Domain of [latex]\scriptsize {{h}^{{-1}}}(x)[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R}\}\text{ }[/latex]
Range of [latex]\scriptsize {{h}^{{-1}}}(x)[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R}\}\text{ }[/latex] - The graphs of [latex]\scriptsize h(x)[/latex] and [latex]\scriptsize {{h}^{{-1}}}(x)[/latex] are symmetrical about the line [latex]\scriptsize y=x[/latex].
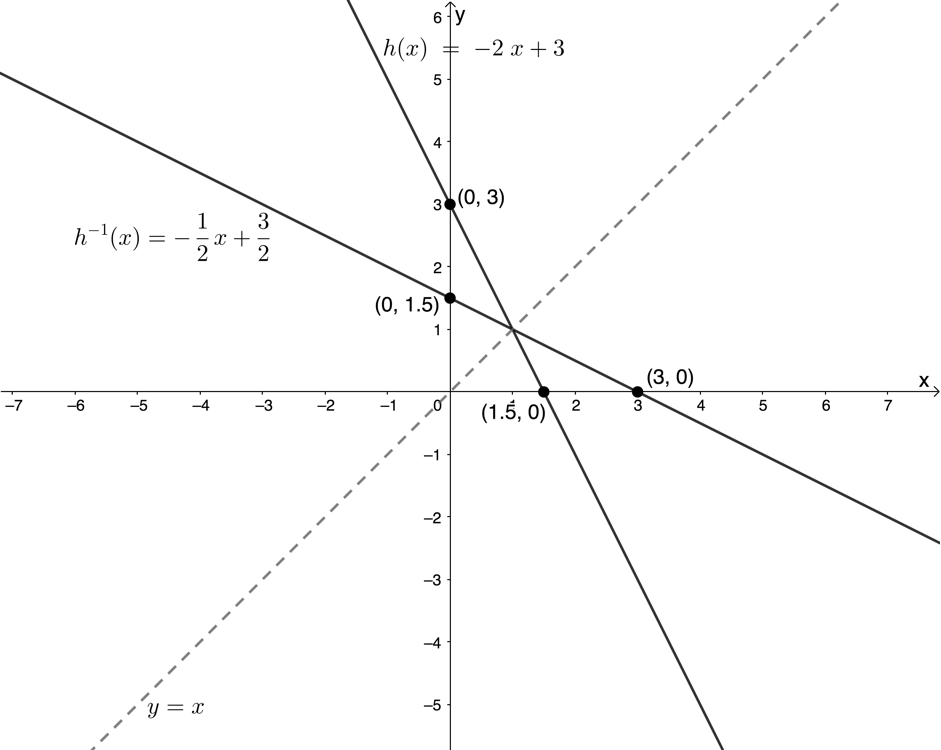
In Example 1.2, we saw that the graphs of [latex]\scriptsize h(x)[/latex] and its inverse [latex]\scriptsize {{h}^{{-1}}}(x)[/latex] are symmetrical about the line [latex]\scriptsize y=x[/latex]. This makes sense given the fact that we found the equation for [latex]\scriptsize {{h}^{{-1}}}(x)[/latex] by interchanging [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex].
This symmetry was also visible in the intercepts of each graph with the axes. The y-intercept of [latex]\scriptsize h(x)[/latex] became the x-intercept of [latex]\scriptsize {{h}^{{-1}}}(x)[/latex] and the x-intercept of [latex]\scriptsize h(x)[/latex] became the y-intercept of [latex]\scriptsize {{h}^{{-1}}}(x)[/latex].
Exercise 1.2
- Given [latex]\scriptsize f(x)=-2x+3[/latex]:
- Find [latex]\scriptsize {{f}^{{-1}}}(x)[/latex]
- Find [latex]\scriptsize \displaystyle {{\left[ {f(x)} \right]}^{{-1}}}[/latex]
- Consider the relation [latex]\scriptsize y=\displaystyle \frac{3}{4}x+\displaystyle \frac{1}{2}[/latex]:
- Is the relation a function?
- Determine the inverse of this relation.
- Is this relation an invertible function?
- Given [latex]\scriptsize q(x)=2x+1[/latex]:
- Determine [latex]\scriptsize {{q}^{{-1}}}(x)[/latex].
- Sketch the graphs of [latex]\scriptsize q(x)[/latex] and [latex]\scriptsize {{q}^{{-1}}}(x)[/latex] on the same system of axes.
- If [latex]\scriptsize S(2,5)[/latex] is a point on [latex]\scriptsize q(x)[/latex], determine the coordinates of [latex]\scriptsize T[/latex] if [latex]\scriptsize T[/latex] is a point on [latex]\scriptsize {{q}^{{-1}}}(x)[/latex] and if [latex]\scriptsize S[/latex] and [latex]\scriptsize T[/latex] are symmetrical.
- Given [latex]\scriptsize {{t}^{{-1}}}(x)=-3x-3[/latex]:
- Determine [latex]\scriptsize t(x)[/latex].
- Determine the intercepts with the axes of [latex]\scriptsize t(x)[/latex] and [latex]\scriptsize {{t}^{{-1}}}(x)[/latex].
- Determine the coordinates of [latex]\scriptsize A[/latex], the point of intersection of [latex]\scriptsize t(x)[/latex] and [latex]\scriptsize {{t}^{{-1}}}(x)[/latex].
- If [latex]\scriptsize f(x)=3x-2[/latex], is [latex]\scriptsize {{f}^{{-1}}}(x)[/latex] an increasing or decreasing function? Explain your answer.
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- A relation is a mathematical rule that associates elements of one set (the inputs or independent variables) with at least one element of a second set (the outputs or dependent variables).
- The set of inputs is called the domain and the set of outputs is called the range.
- A function is a special type of relation such that each input is associated with one and only one output.
- Functions can be one-to-one or many-to one.
- The inverse of a function performs the reverse operation of a function.
- If the inverse of a function is also a function, then the function is said to be invertible.
- If the inverse of a function [latex]\scriptsize f(x)[/latex] is a function it can be represented with inverse function notation [latex]\scriptsize {{f}^{{-1}}}(x)[/latex].
Unit 1: Assessment
Suggested time to complete: 15 minutes
Question 1 adapted from NC(V) Mathematics Level 4 Paper 1 November 2011
- The diagram below represents the graph of [latex]\scriptsize f(x)=2x+3[/latex]:
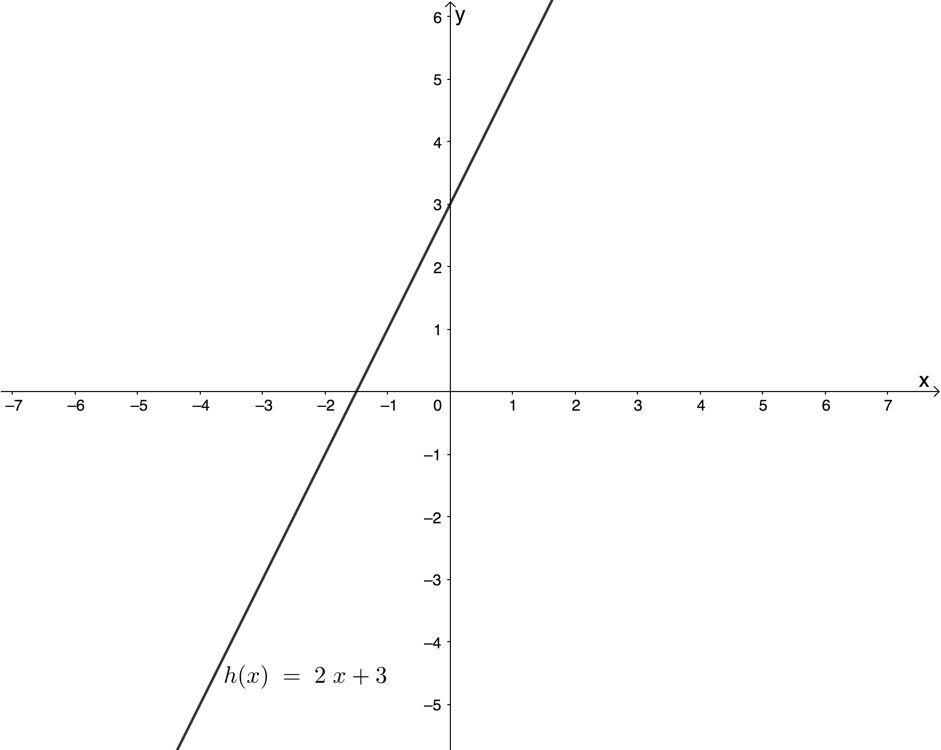
- Determine [latex]\scriptsize {{f}^{{-1}}}[/latex], the inverse of [latex]\scriptsize f[/latex] in the form [latex]\scriptsize y=[/latex].
- Draw the graph of [latex]\scriptsize {{f}^{{-1}}}[/latex].
- Given [latex]\scriptsize f(x)=\displaystyle \frac{1}{2}x-1[/latex], find:
- [latex]\scriptsize {{f}^{{-1}}}(x)[/latex]
- [latex]\scriptsize \displaystyle {{\left[ {f(x)} \right]}^{{-1}}}[/latex]
- Given [latex]\scriptsize {{h}^{{-1}}}(x)=\displaystyle \frac{1}{3}x+2[/latex]:
- Determine [latex]\scriptsize h(x)[/latex].
- Determine the intercepts with the axes of [latex]\scriptsize h(x)[/latex] and [latex]\scriptsize {{h}^{{-1}}}(x)[/latex].
- Determine the coordinates of [latex]\scriptsize Q[/latex] the point of intersection of [latex]\scriptsize h(x)[/latex] and [latex]\scriptsize {{h}^{{-1}}}(x)[/latex].
- State the domain and range of [latex]\scriptsize h(x)[/latex] and [latex]\scriptsize {{h}^{{-1}}}(x)[/latex].
- Sketch the graphs of [latex]\scriptsize h(x)[/latex] and [latex]\scriptsize {{h}^{{-1}}}(x)[/latex] on the same set of axes showing the intercepts with the axes and the point of intersection.
- Is [latex]\scriptsize h(x)[/latex] an increasing or decreasing function?
The full solutions are at the end of the unit.
Unit 1: Solutions
Exercise 1.1
- Not a function
- Function
- Function
- Function
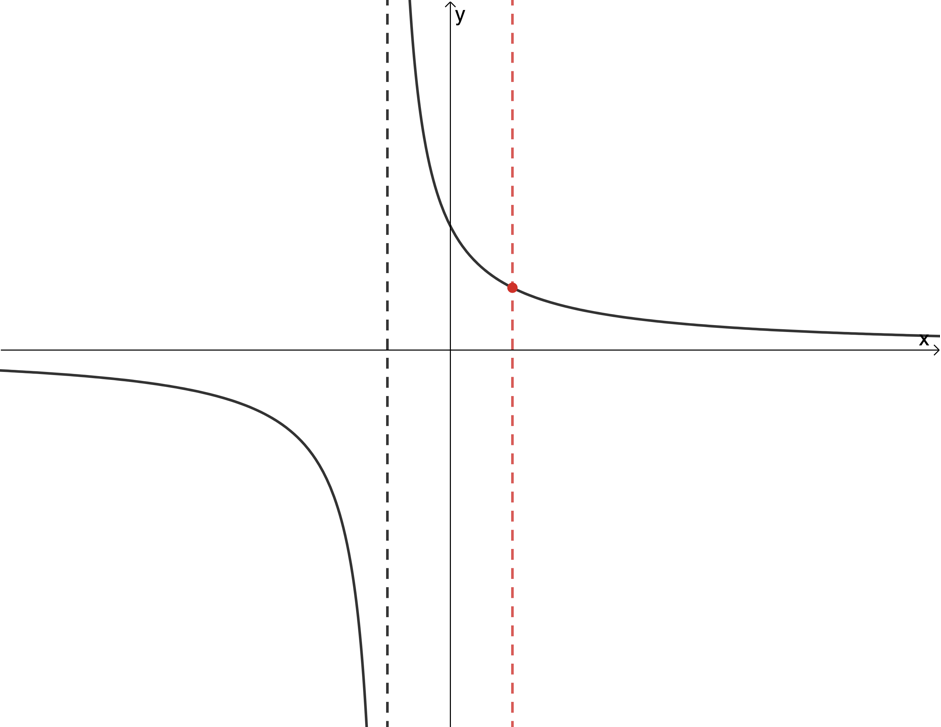
- Not a function

- Function
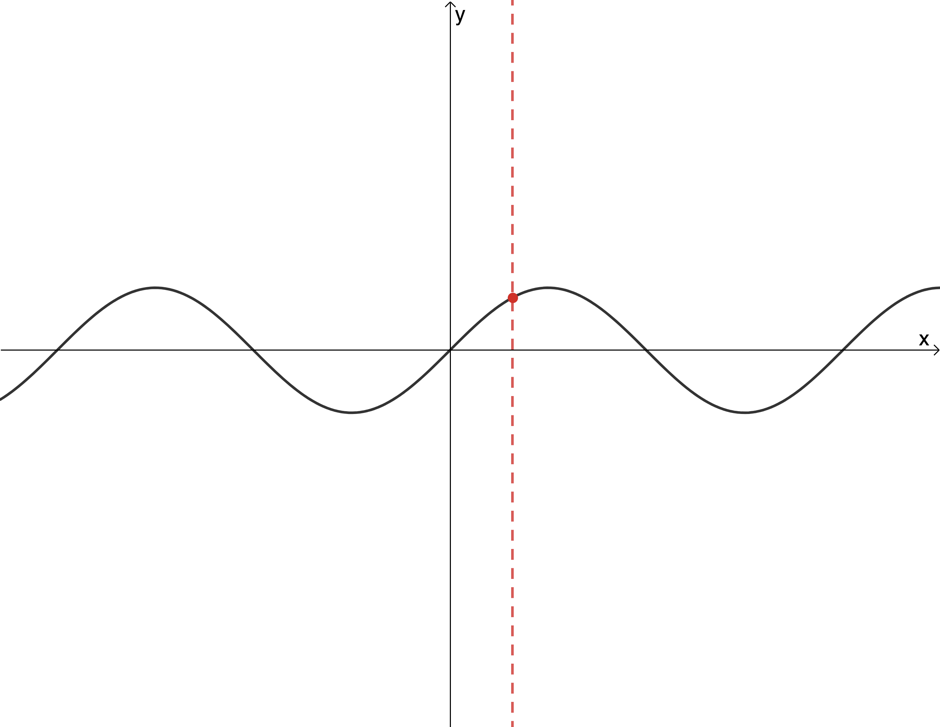
- Not a function
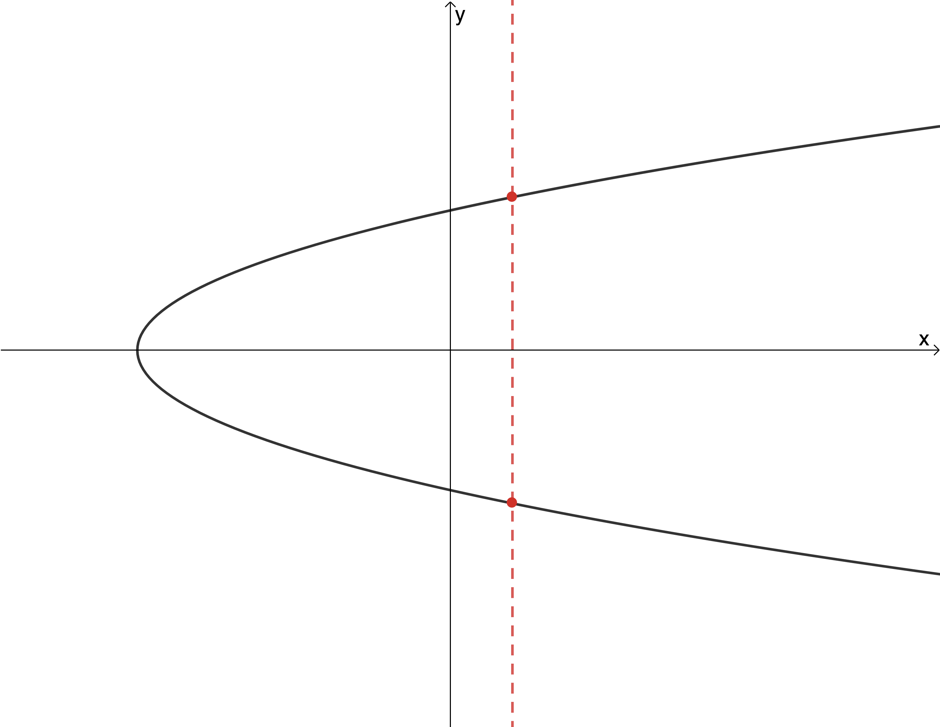
- Not a function
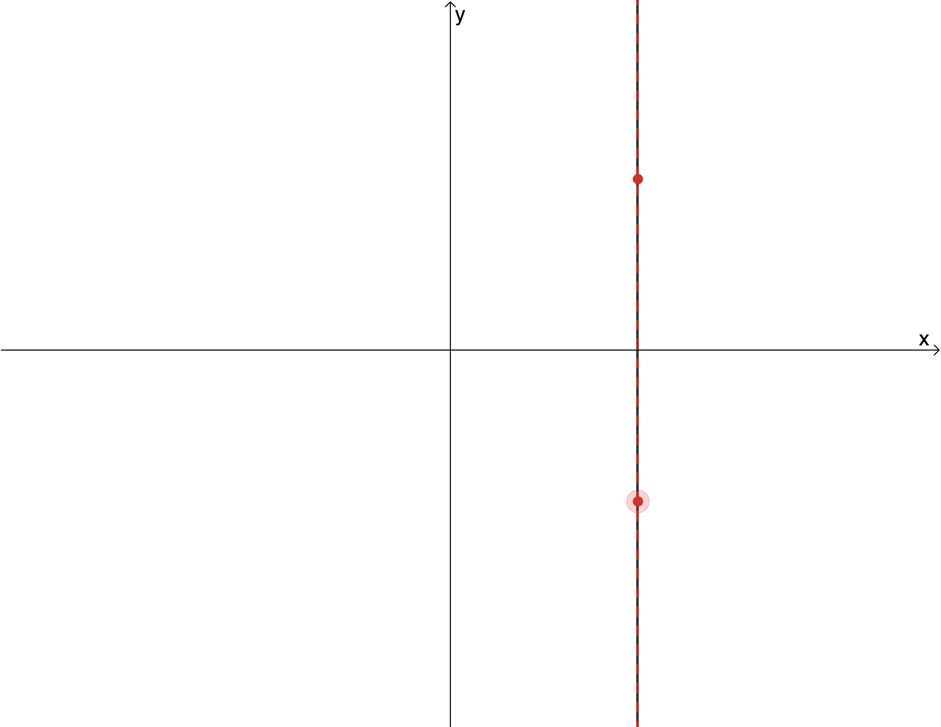
- Function

- Function

Exercise 1.2
- [latex]\scriptsize f(x)=-2x+3[/latex]
- [latex]\scriptsize y=-2x+3[/latex]
Inverse:
[latex]\scriptsize \begin{align*}x & =-2y+3\\\therefore 2y & =-x+3\\\therefore y & =-\displaystyle \frac{1}{2}x+\displaystyle \frac{3}{2}\\\therefore {{f}^{{-1}}}(x) & =-\displaystyle \frac{1}{2}x+\displaystyle \frac{3}{2}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{\left[ {f(x)} \right]}^{{-1}}}&=\displaystyle \frac{1}{{f(x)}}\\&=\displaystyle \frac{1}{{-2x+3}}\\&=-\displaystyle \frac{1}{{2x-3}}\end{align*}[/latex]
- [latex]\scriptsize y=-2x+3[/latex]
- [latex]\scriptsize y=\displaystyle \frac{3}{4}x+\displaystyle \frac{1}{2}[/latex].
- The relation is a linear function.
- .
[latex]\scriptsize \begin{align*} x&=\displaystyle \frac{3}{4}y+\displaystyle \frac{1}{2}\\ \therefore \displaystyle \frac{3}{4}y&=x+\displaystyle \frac{1}{2}\\ \therefore 3y&=4x-2\\ \therefore y&=\displaystyle \frac{4}{3}x-\displaystyle \frac{2}{3}\end{align*}[/latex] - The inverse of the function is also a function. Therefore, the relation is an invertible function.
- [latex]\scriptsize q(x)=2x+1[/latex].
- [latex]\scriptsize y=2x+1[/latex]
Inverse:
[latex]\scriptsize \begin{align*}x & =2y+1\\\therefore 2y & =x-1\\\therefore y & =\displaystyle \frac{1}{2}x-\displaystyle \frac{1}{2}\\\therefore {{q}^{{-1}}}(x) & =\displaystyle \frac{1}{2}x-\displaystyle \frac{1}{2}\end{align*}[/latex] - .
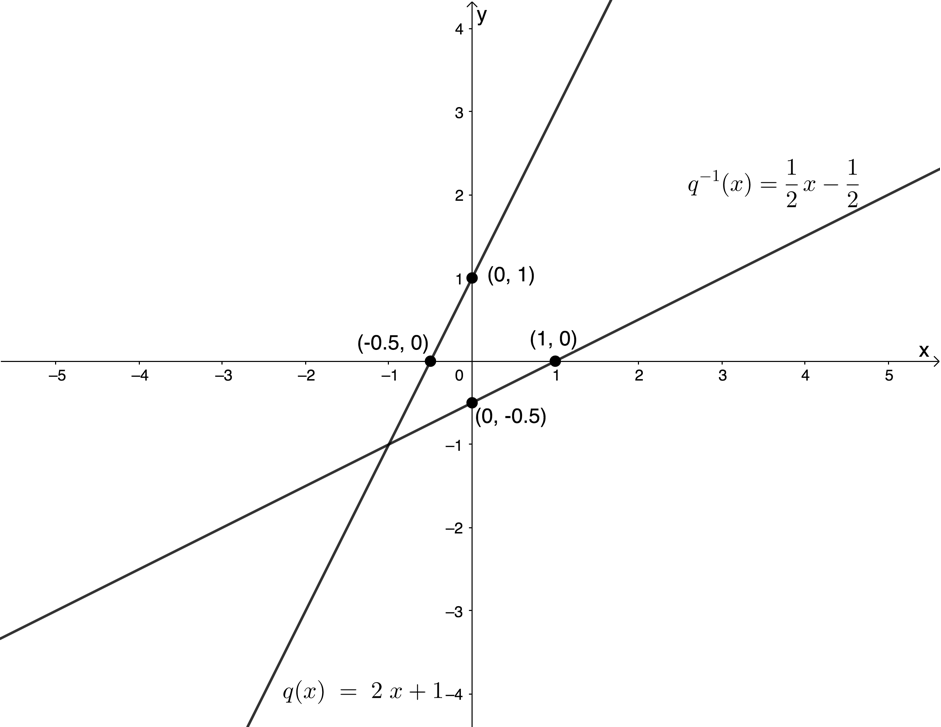
- [latex]\scriptsize q(x)[/latex] and [latex]\scriptsize {{q}^{{-1}}}(x)[/latex] are symmetrical about the line [latex]\scriptsize y=x[/latex]. Therefore, [latex]\scriptsize T[/latex] is the point [latex]\scriptsize (5,2)[/latex].
- [latex]\scriptsize y=2x+1[/latex]
- [latex]\scriptsize {{t}^{{-1}}}(x)=-3x-3[/latex]
- [latex]\scriptsize t(x)[/latex] is the inverse of [latex]\scriptsize {{t}^{{-1}}}(x)[/latex].
[latex]\scriptsize y=-3x-3[/latex]
Inverse:
[latex]\scriptsize \begin{align*}x & =-3y-3\\\therefore 3y & =-x-3\\\therefore y & =-\displaystyle \frac{1}{3}x-1\\\therefore t(x) & =-\displaystyle \frac{1}{3}x-1\end{align*}[/latex] - [latex]\scriptsize t(x)=-\displaystyle \frac{1}{3}x-1[/latex]
x-intercept (let [latex]\scriptsize t(x)=0[/latex]):
[latex]\scriptsize \begin{align*} -\displaystyle \frac{1}{3}x-1&=0\\ \therefore \displaystyle \frac{1}{3}x&=-1\\ \therefore x&=-3 \end {align*}[/latex]
x-intercept is the point [latex]\scriptsize (-3,0)[/latex]
y-intercept (let [latex]\scriptsize x=0[/latex]):
[latex]\scriptsize \begin{align*}t(0) & =-\displaystyle \frac{1}{3}(0)-1\\\therefore t(0) & =-1\end{align*}[/latex]
y-intercept is the point [latex]\scriptsize (0,-1)[/latex]
[latex]\scriptsize {{t}^{{-1}}}(x)=-3x-3[/latex]:
[latex]\scriptsize {{t}^{{-1}}}(x)[/latex] is the inverse of [latex]\scriptsize t(x)[/latex]. Therefore x-intercept of [latex]\scriptsize {{t}^{{-1}}}(x)[/latex] is [latex]\scriptsize (-1,0)[/latex] and y-intercept of [latex]\scriptsize {{t}^{{-1}}}(x)[/latex] is [latex]\scriptsize (0,-3)[/latex].
Note: You could also have calculated the intercepts directly. - .
[latex]\scriptsize \begin{align*} t(x)&=t^{-1}(x)\\ \therefore -\displaystyle \frac{1}{3}x-1&=-3x-3\\ \therefore -x-3&=-9x-9\\ \therefore 8x&=-6\\ \therefore x&=-\displaystyle \frac{3}{4} \end{align*}[/latex]
[latex]\scriptsize \begin{align*}t\left( {-\displaystyle \frac{3}{4}} \right)&=-\displaystyle \frac{1}{3}\left( {-\displaystyle \frac{3}{4}} \right)-1\\&=\displaystyle \frac{3}{{12}}-1\\&=\displaystyle \frac{1}{4}-1\\&=-\displaystyle \frac{3}{4}\end{align*}[/latex]
[latex]\scriptsize A[/latex] is the point [latex]\scriptsize (-\displaystyle \frac{3}{4},-\displaystyle \frac{3}{4})[/latex]
- [latex]\scriptsize t(x)[/latex] is the inverse of [latex]\scriptsize {{t}^{{-1}}}(x)[/latex].
- [latex]\scriptsize f(x)=3x-2[/latex] is an increasing function. Therefore, [latex]\scriptsize {{f}^{{-1}}}(x)[/latex] is an increasing function as it is symmetrical to [latex]\scriptsize f(x)[/latex] about the line [latex]\scriptsize y=x[/latex], an increasing function.
Unit 1: Assessment
- .
- [latex]\scriptsize f(x)=\displaystyle \frac{1}{2}x-1[/latex]
- [latex]\scriptsize y=\displaystyle \frac{1}{2}x-1[/latex]
[latex]\scriptsize {{f}^{{-1}}}(x)[/latex]:
[latex]\scriptsize \begin{align*}x & =\displaystyle \frac{1}{2}y-1\\\therefore \displaystyle \frac{1}{2}y & =x+1\\\therefore y & =2x+2\\\therefore {{f}^{{-1}}}(x) & =2x+2\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}{{\left[ {f(x)} \right]}^{{-1}}}&=\displaystyle \frac{1}{{f(x)}}\\&=\displaystyle \frac{1}{{\left( {\displaystyle \frac{1}{2}x-1} \right)}}\\&=\displaystyle \frac{1}{{\left( {\displaystyle \frac{{x-2}}{2}} \right)}}\\&=\displaystyle \frac{2}{{x-2}}\end{align*}[/latex]
- [latex]\scriptsize y=\displaystyle \frac{1}{2}x-1[/latex]
- [latex]\scriptsize {{h}^{{-1}}}(x)=\displaystyle \frac{1}{3}x+2[/latex].
- [latex]\scriptsize y=\displaystyle \frac{1}{3}x+2[/latex]
[latex]\scriptsize h(x)[/latex]:
[latex]\scriptsize \begin{align*}x & =\displaystyle \frac{1}{3}y+2\\\therefore \displaystyle \frac{1}{3}y & =x-2\\\therefore y & =3x-6\\\therefore h(x) & =3x-6\end{align*}[/latex] - [latex]\scriptsize h(x)[/latex]:
x-intercept (let [latex]\scriptsize h(x)=0[/latex]):
[latex]\scriptsize \begin {align*} 3x-6&=0\\ \therefore 3x&=6\\ \therefore x&=2 \end{align*}[/latex]
x-intercept is the point [latex]\scriptsize (2,0)[/latex]
y-intercept (let [latex]\scriptsize x=0[/latex]):
[latex]\scriptsize \begin{align*}h(0) & =3(0)-6\\\therefore h(0) & =-6\end{align*}[/latex]
y-intercept is the point [latex]\scriptsize (0,-6)[/latex]
[latex]\scriptsize {{h}^{{-1}}}(x)[/latex]:
[latex]\scriptsize {{h}^{{-1}}}(x)[/latex] is the inverse of [latex]\scriptsize h(x)[/latex]. Therefore, the x-intercept of [latex]\scriptsize {{h}^{{-1}}}(x)[/latex] is [latex]\scriptsize (-6,0)[/latex] and y-intercept of [latex]\scriptsize {{t}^{{-1}}}(x)[/latex] is [latex]\scriptsize (0,2)[/latex] - .
[latex]\scriptsize \begin{align*}h(x) & ={{h}^{{-1}}}(x)\\\therefore 3x-6 & =\displaystyle \frac{1}{3}x+2\\\therefore 9x-18 & =x+6\\\therefore 8x & =24\\\therefore x & =3\end{align*}[/latex]
[latex]\scriptsize \begin{align*}h(3)&=3(3)-6\\&=9-6\\&=3\end{align*}[/latex]
[latex]\scriptsize Q[/latex] is the point [latex]\scriptsize (3,3)[/latex]. - Domain of [latex]\scriptsize h(x)[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R}\}\text{ }[/latex]
Range of [latex]\scriptsize h(x)[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R}\}\text{ }[/latex]
Domain of [latex]\scriptsize {{h}^{{-1}}}(x)[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R}\}\text{ }[/latex]
Domain of [latex]\scriptsize {{h}^{{-1}}}(x)[/latex]: [latex]\scriptsize \{x|x\in \mathbb{R}\}\text{ }[/latex] - .
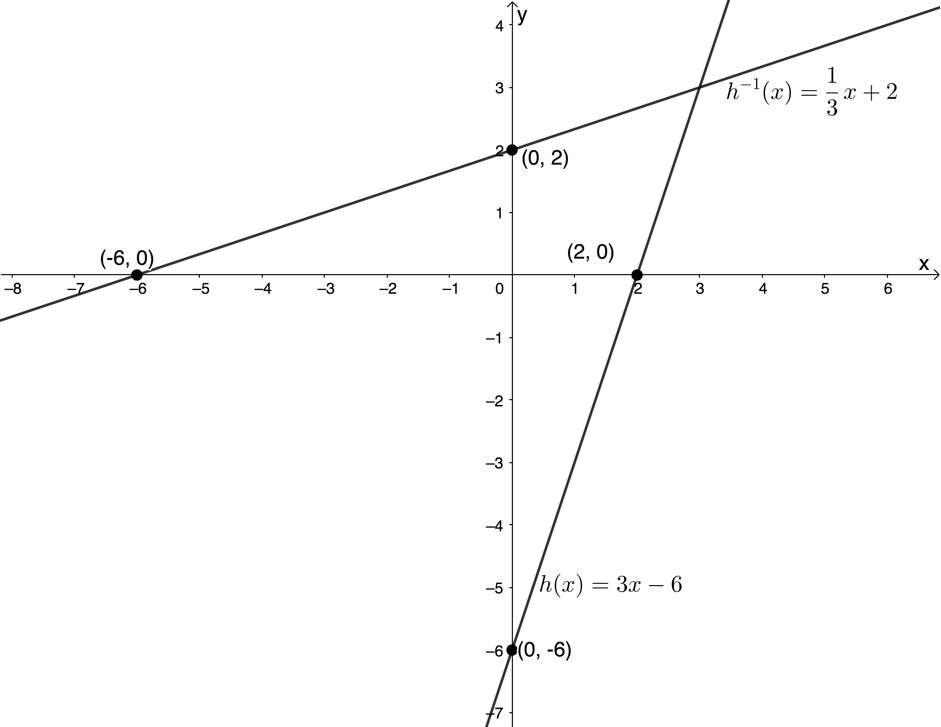
- [latex]\scriptsize h(x)[/latex] is an increasing function. The function value increase as x increases.
- [latex]\scriptsize y=\displaystyle \frac{1}{3}x+2[/latex]
Media Attributions
- Functions in relations © DHET is licensed under a CC BY (Attribution) license
- Figure 4 © DHET is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- Input output example 1 © DHET is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure6 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure7 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q6 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q7 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q8 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q9 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 Q10 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure8 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure9 © Geogebra is licensed under a CC BY (Attribution) license
- example1.2 A2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example1.2 A4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment Q1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 A1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 A2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 A3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 A4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 A5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 A6 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 A7 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 A8 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 A9 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.1 A10 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.2 A3b © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment A1b © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessment A3e © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license