Unit outcomes

By the end of this unit you will be able to:

• Find the gradient of a tangent to a circle using analytical geometry.
• Find the equation of a tangent to the circle using analytical geometry.
• Find the equation of a tangent to a circle at the point of contact with the radius.

What you should know

Before you start this unit, make sure you can:

• Find the equations of straight lines using the two-point form, the gradient-point form or the gradient-intercept form, depending on the information available. Refer to level 3 subject outcome 3.2 unit 1 if you need help with this.
• Find the equations of parallel and perpendicular lines. Refer to level 3 subject outcome 3.2 unit 2 if you need help with this.

Introduction

From your work on limits, instantaneous rates of change and calculus, you are aware of what a tangent is (not to be confused with the trigonometric function tangent). The word ‘tangent’ comes from the Latin verb ‘tangere’ which means ‘to touch’ and this exactly describes what a tangent is. It is a straight line that another curve just touches at one point. It does not cross or intersect. It only touches at one point.

Consider the quadratic function [latex]\scriptsize f(x)={{(x-2)}^{2}}[/latex]. The parabola touches the x-axis at the point [latex]\scriptsize (2,0)[/latex] (see figure 1). It does not cross the x-axis or touch it at more than one point. It touches it only at this point. We say that the x-axis is a tangent to the function [latex]\scriptsize f(x)={{(x-2)}^{2}}[/latex] at the point [latex]\scriptsize (2,0)[/latex].

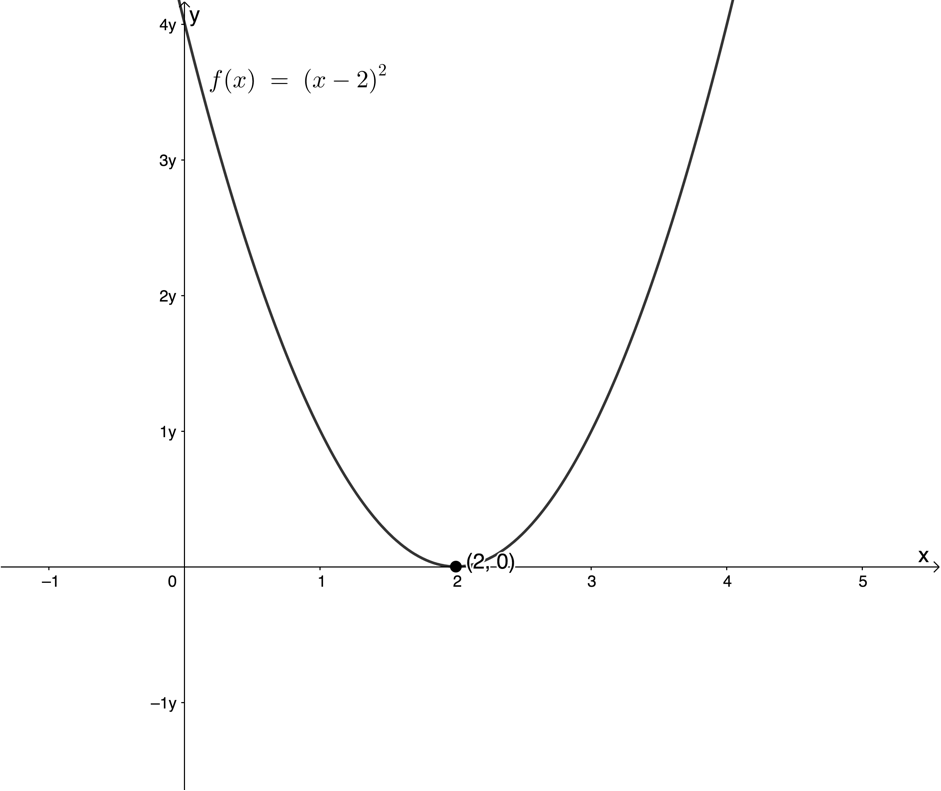
Of course, the function [latex]\scriptsize f(x)={{(x-2)}^{2}}[/latex] does not only have this single tangent. It has infinitely many different tangents, each of which touches the parabola at one point. When we calculate the limit of a function such as [latex]\scriptsize f(x)={{(x-2)}^{2}}[/latex] at a certain point we are calculating the gradient of the tangent to the curve at that point, which we take as the gradient of the curve itself at that point.

Now it is possible to use the techniques and methods of calculus to find the gradient of a tangent to a circle at any point but, because the circle is not a function, this is quite complicated. However, we can use analytical geometry to do this in a much simpler way.

The gradient of the tangent to a circle

Finding the gradient of a tangent to a circle at any point on the circle using analytical geometry is quite straightforward. But it relies on understanding the relationship of the tangent to the radius of the circle at the point of tangency. Let’s investigate.

Activity 2.1: The tangent and the radius

Time required: 5 minutes

What you need:

• a pen or pencil

What to do:

In figure 2 is a sketch of the circle [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=25[/latex]. On the circle is the point [latex]\scriptsize T(3,4)[/latex]. Touching the circle at point [latex]\scriptsize T[/latex] is a tangent to the circle. [latex]\scriptsize P(7,1)[/latex] is a point on the tangent line.

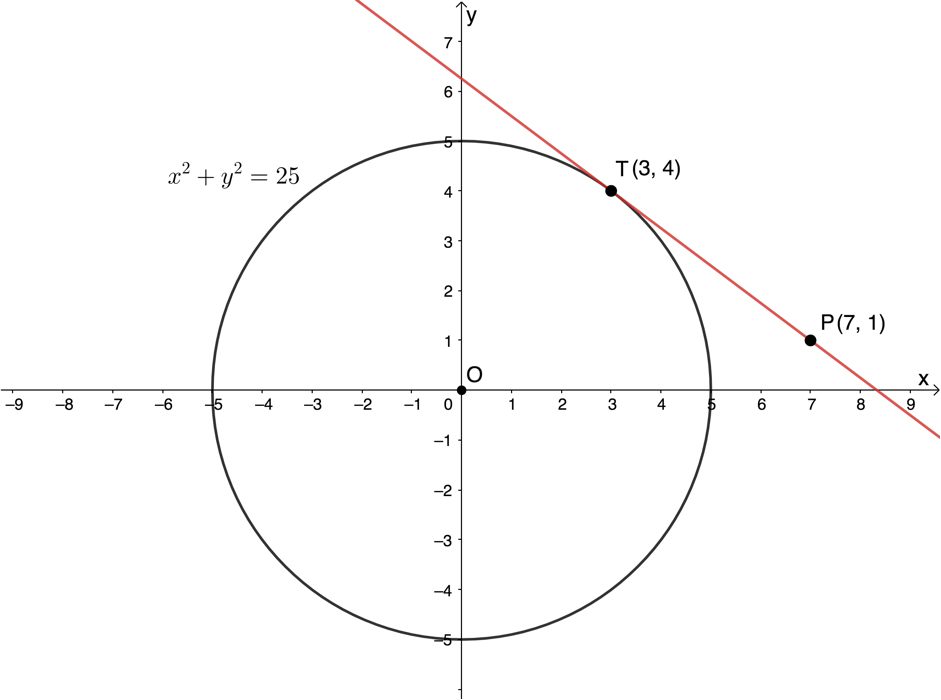
1. Determine the gradient of the tangent line [latex]\scriptsize PT[/latex].
2. Determine the gradient of the radius [latex]\scriptsize OT[/latex].
3. What can you say about the lines [latex]\scriptsize PT[/latex] and [latex]\scriptsize OT[/latex]?
4. What can you say generally about a tangent and a radius of the circle at the point of tangency?

What did you find?

1. .
   [latex]\scriptsize \begin{align*}{{m}_{{PT}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{4-1}}{{3-7}}\\&=-\displaystyle \frac{3}{4}\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}{{m}_{{OT}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{4-0}}{{3-0}}\\&=\displaystyle \frac{4}{3}\end{align*}[/latex]
3. Because [latex]\scriptsize {{m}_{{PT}}}\times {{m}_{{OT}}}=-1[/latex] we can say that the lines [latex]\scriptsize PT[/latex] and [latex]\scriptsize OT[/latex] are perpendicular.
4. In general, the tangent to a circle is perpendicular to the radius of the circle at that point.

From activity 2.1 we see that the radius of a tangent is perpendicular to the tangent at the point of contact (or tangency).

Take note!

The radius [latex]\scriptsize r[/latex] of a circle centre [latex]\scriptsize C(a,b)[/latex] is perpendicular to the tangent to the circle [latex]\scriptsize PT[/latex] at the point of tangency [latex]\scriptsize T(x,y)[/latex].

Example 2.1

Find the gradient of the tangent to the circle [latex]\scriptsize 2{{x}^{2}}+16x+2{{y}^{2}}-4y=34[/latex] at the point [latex]\scriptsize T(-1,2)[/latex].

Solution

In order to find the gradient of the tangent to the circle at the point [latex]\scriptsize T(-1,2)[/latex], we need to find the gradient of the radius of the circle to this point. To start, we must get our circle equation into standard form so that we can determine the centre of the circle.

[latex]\scriptsize \begin{align*}2{{x}^{2}}+16x+2{{y}^{2}}-4y & =34\quad \text{Get the coefficients of }{{x}^{2}}\text{ and }{{y}^{2}}\text{ terms equal to }1\\\therefore {{x}^{2}}+8x+{{y}^{2}}-2y & =17\quad \text{Complete the squares}\\\therefore {{x}^{2}}+8x+16+{{y}^{2}}-2y+1 & =17+16+1\\\therefore {{(x+4)}^{2}}+{{(y-1)}^{2}} & =34\end{align*}[/latex]

The centre of the circle is [latex]\scriptsize C(-4,1)[/latex]. Now we can find the gradient of [latex]\scriptsize CT[/latex].
[latex]\scriptsize \begin{align*}{{m}_{{CT}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{2}}}}\\&=\displaystyle \frac{{2-1}}{{-1-(-4)}}\\&=\displaystyle \frac{1}{3}\end{align*}[/latex]

We know that the tangent at [latex]\scriptsize T[/latex] is perpendicular to the radius at [latex]\scriptsize T[/latex]. Therefore, the gradient of the tangent at [latex]\scriptsize T[/latex] is [latex]\scriptsize -3[/latex].

Exercise 2.1

Find the gradient of the tangent to the circle [latex]\scriptsize 3{{x}^{2}}+6x-36=-3{{y}^{2}}-12y[/latex] at the following points:

1. [latex]\scriptsize A(0,2)[/latex]
2. [latex]\scriptsize B(-3,-1)[/latex]
3. [latex]\scriptsize C(2,-6)[/latex]
4. [latex]\scriptsize D(5,-3)[/latex]

The full solutions are at the end of the unit.

Find the equation of a tangent to a circle

Now that we know how to find the gradient of a tangent to a circle, we can use this information to help us find the equation of the tangent line.

To find the equations of tangents to circles, we use the same techniques as we learnt in level 3 subject outcome 3.2 unit 1, namely using the following:

• the two-point form
• the gradient–point form
• the gradient–intercept form.

Refer back to this unit now if you need to.

Example 2.2

Determine the equation of the tangent to the circle [latex]\scriptsize {{x}^{2}}+{{y}^{2}}-2y+6x-7=0[/latex] at the point [latex]\scriptsize T(-7,2)[/latex].

Solution

Step 1: Find the centre of the circle
If you don’t know the centre, you need to find it. To do so, we must get the equation into standard form.
[latex]\scriptsize \begin{align*}{{x}^{2}}+{{y}^{2}}-2y+6x-7 & =0\\\therefore {{x}^{2}}+6x+{{y}^{2}}-2y & =7\quad \text{Complete the squares}\\\therefore {{x}^{2}}+6x+9+{{y}^{2}}-2y+1 & =7+9+1\\\therefore {{(x+3)}^{2}}+{{(y-1)}^{2}} & =17\end{align*}[/latex]

The centre of the circle is [latex]\scriptsize C(-3,1)[/latex].

Step 2: Determine the gradient of the radius of the circle to the point of tangency
[latex]\scriptsize \begin{align*}{{m}_{{CT}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{2-1}}{{-7-(-3)}}\\&=-\displaystyle \frac{1}{4}\end{align*}[/latex]

Step 3: Determine the gradient of the tangent
The tangent at [latex]\scriptsize T(-7,2)[/latex] is perpendicular to the radius to [latex]\scriptsize T(-7,2)[/latex]. Therefore, the gradient of the tangent is [latex]\scriptsize 4[/latex].

Step 4: Find the equation of the tangent
We know the gradient of the tangent and a point [latex]\scriptsize T(-7,2)[/latex] that it passes through. Therefore, we can use the gradient-point form.

[latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-2 & =4\left( {x-(-7)} \right)\\\therefore y-2 & =4x+28\\\therefore y & =4x+30\end{align*}[/latex]

The equation of the tangent at [latex]\scriptsize T(-7,2)[/latex] is [latex]\scriptsize y=4x+30[/latex].

Exercise 2.2

1. A circle with centre [latex]\scriptsize C(2,-2)[/latex] has a tangent at [latex]\scriptsize A(-2,-1)[/latex]. Find the equation of the tangent.
2. [latex]\scriptsize C(3,4)[/latex] is the centre of the circle passing through [latex]\scriptsize S(-2,1)[/latex] and [latex]\scriptsize T(6,p)[/latex].
   
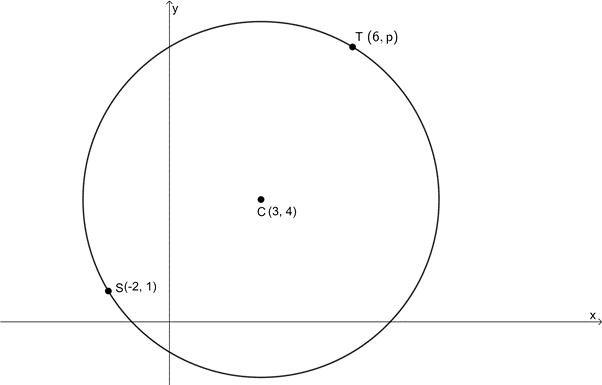
   1. Determine the equation of the circle.
   2. Determine the value of [latex]\scriptsize p[/latex].
   3. Determine the equation of the tangent at [latex]\scriptsize T[/latex].

Question 3 adapted from Everything Maths Grade 12 Worked example 14

3. Determine the equations of the tangents to the circle [latex]\scriptsize {{x}^{2}}+{{(y-1)}^{2}}=80[/latex] if they are both parallel to the line [latex]\scriptsize y=\displaystyle \frac{1}{2}x+1[/latex].

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• That the tangent to a circle is perpendicular to the radius of the circle at the point of tangency.

Unit 2: Assessment

Suggested time to complete: 50 minutes

Question 1 adapted from NC(V) Mathematics Level 4 Paper 2 November 2013 question 1.5

1. Points [latex]\scriptsize A(-3,-2)[/latex] and [latex]\scriptsize B(1,4)[/latex] lie on a circle such that [latex]\scriptsize AB[/latex] is a diameter of the circle.
   
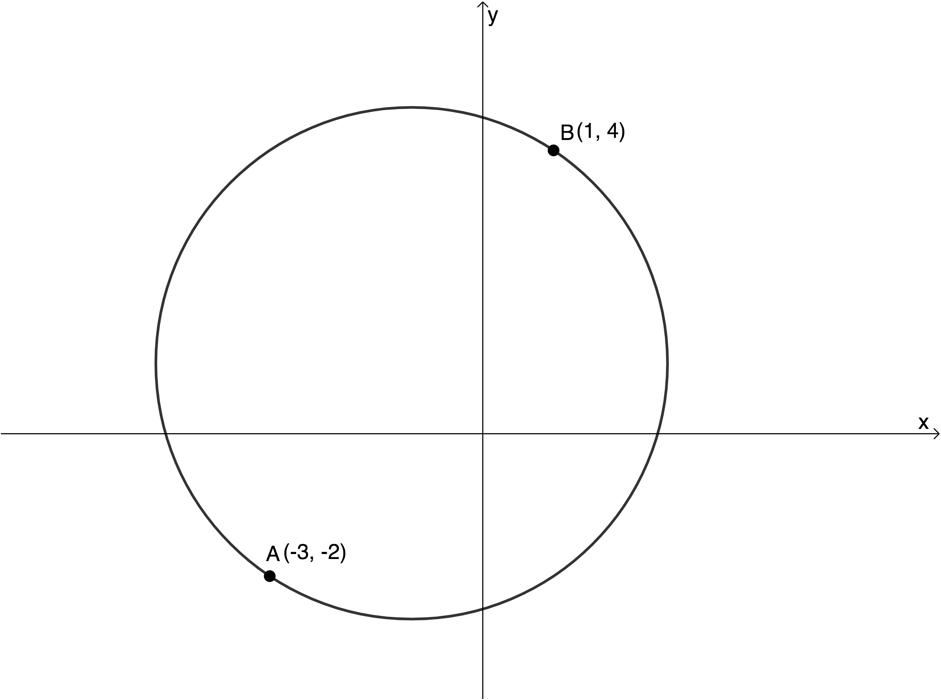
   1. Determine the equation of the circle.
   2. Determine the tangent to the circle at [latex]\scriptsize A[/latex].

Question 2 adapted from NC(V) Mathematics Level 4 Paper 2 November 2012 question 1.4

2. In the diagram below a circle with centre [latex]\scriptsize M(3,1)[/latex] is given. [latex]\scriptsize A[/latex] is a point on the y-axis. [latex]\scriptsize AB[/latex] is the diameter of the circle and [latex]\scriptsize CD[/latex] is a tangent to the circle at [latex]\scriptsize B(6,-3)[/latex].
   
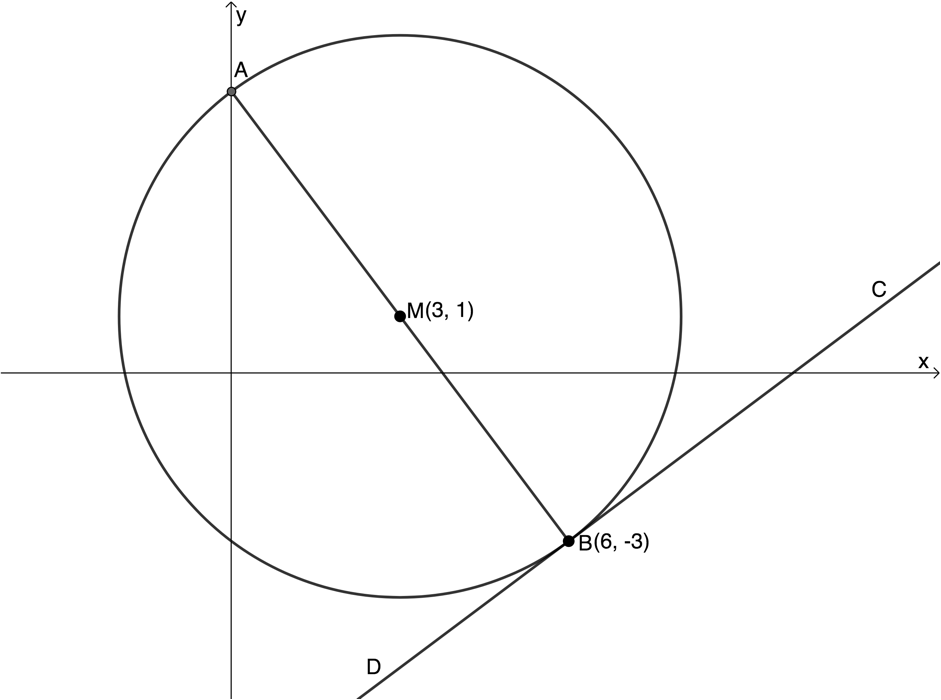
   1. Determine the coordinates of point [latex]\scriptsize A[/latex].
   2. Determine the equation of the tangent to the circle at [latex]\scriptsize B[/latex].

Question 3 adapted from NC(V) Mathematics Level 4 Paper 2 November 2014 question 1.5

3. In the diagram below [latex]\scriptsize A(-1,-5)[/latex] is a point on the circle with centre [latex]\scriptsize B(1,-1)[/latex]. The line [latex]\scriptsize FG[/latex] is a tangent to the circle at point [latex]\scriptsize A[/latex].
   
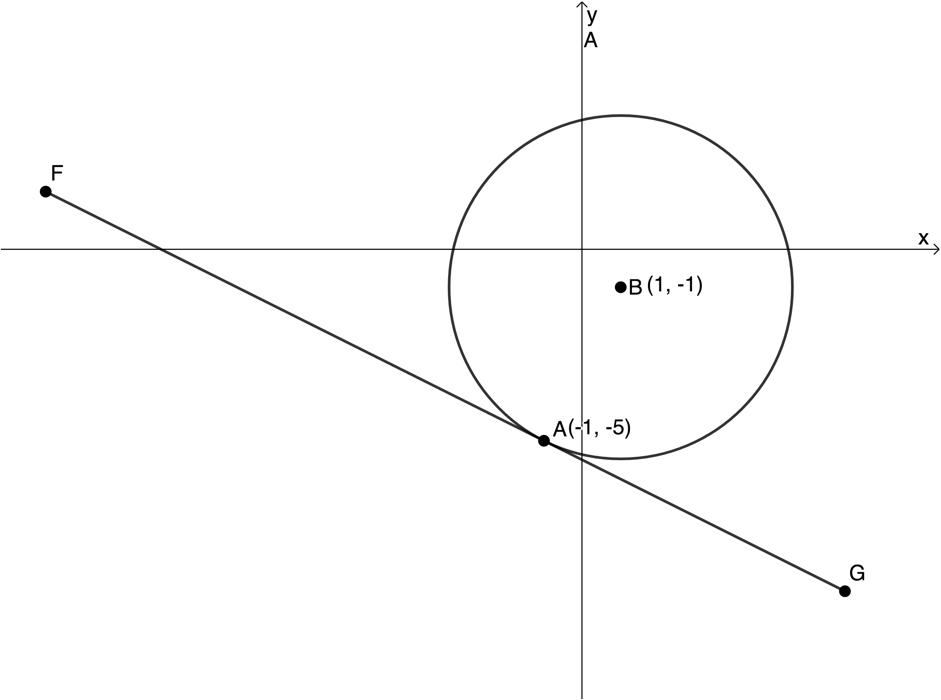
   1. Determine the equation of [latex]\scriptsize FG[/latex].
   2. Determine the equation of the circle.
   3. If the distance from [latex]\scriptsize F[/latex] to [latex]\scriptsize B[/latex] is [latex]\scriptsize \sqrt{{69}}\text{ units}[/latex], determine the length of [latex]\scriptsize FA[/latex].

Question 4 adapted from NC(V) Mathematics Level 4 Paper 2 November 2015 question 1.4

4. A circle with centre [latex]\scriptsize M(-4,2)[/latex] has the points [latex]\scriptsize O(0,0)[/latex] and [latex]\scriptsize N(-2,y)[/latex] on the circumference. The tangents at [latex]\scriptsize O[/latex] and [latex]\scriptsize N[/latex] meet at [latex]\scriptsize P[/latex].
   
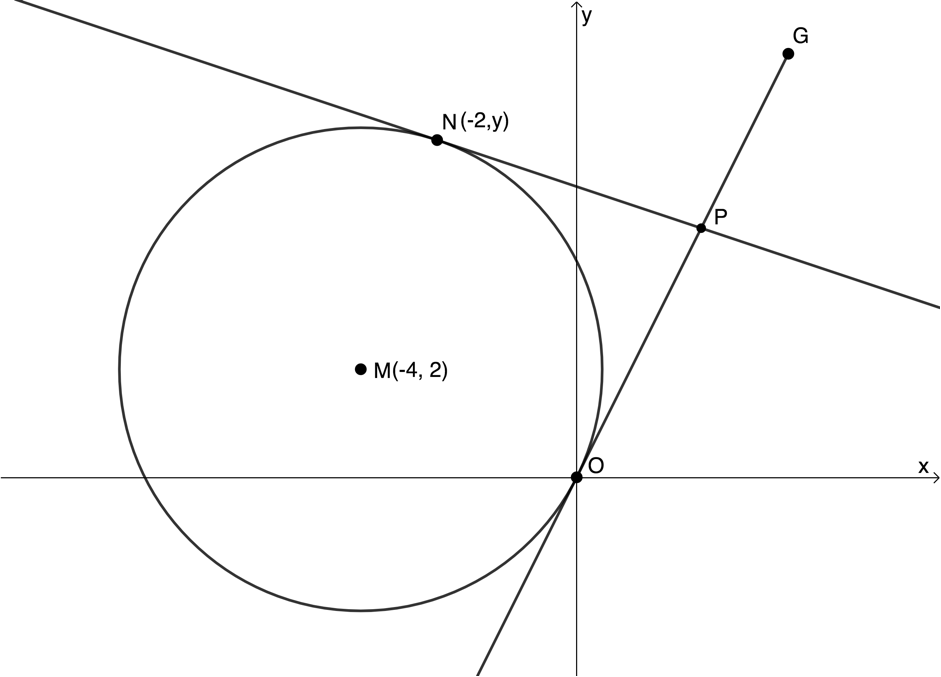
   1. Determine the equation of the circle.
   2. Determine the value of [latex]\scriptsize y[/latex].
   3. Determine the gradient of [latex]\scriptsize OP[/latex].

Question 5 adapted from NC(V) Mathematics Level 4 Paper 2 November 2011 question 1.4

5. The equation of the circle with centre [latex]\scriptsize O[/latex] is [latex]\scriptsize {{x}^{2}}+{{y}^{2}}=36[/latex]. Circle [latex]\scriptsize O[/latex] cuts the x-axis at [latex]\scriptsize S[/latex], and [latex]\scriptsize Q[/latex] is the point [latex]\scriptsize (2,a)[/latex]. [latex]\scriptsize R(m,n)[/latex] is a point in the first quadrant.
   
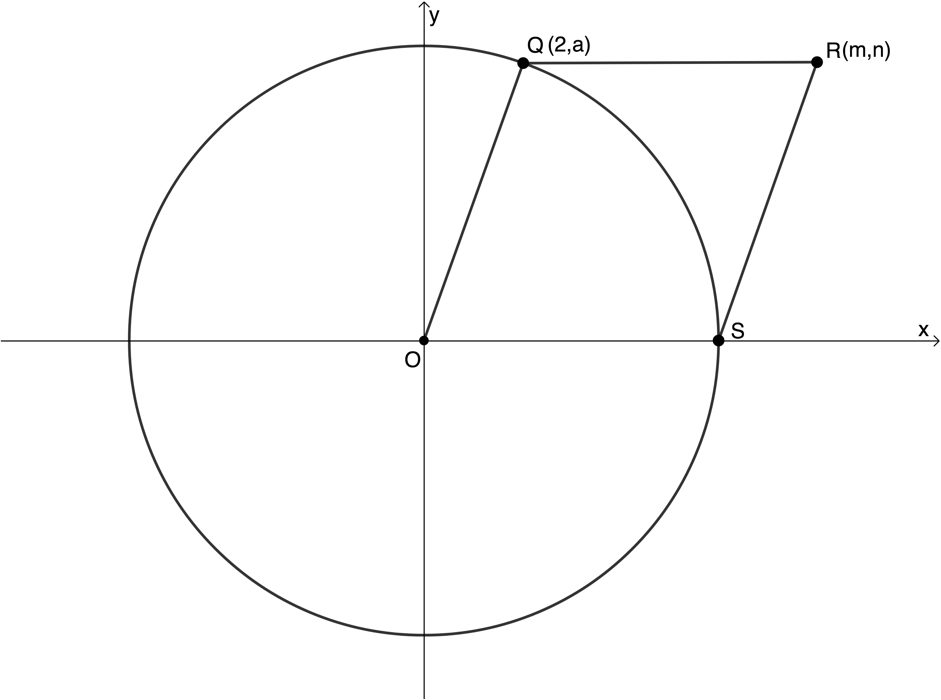
   1. Write down the length of the radius of the circle.
   2. Calculate the value of [latex]\scriptsize a[/latex] and leave the answer in surd form.
   3. Determine the coordinates of [latex]\scriptsize R[/latex] if [latex]\scriptsize OQRS[/latex] is a parallelogram.

The full solutions are at the end of the unit.

Unit 2: Solutions

Exercise 2.1

The equation of the circle is [latex]\scriptsize 3{{x}^{2}}+6x-36=-3{{y}^{2}}-12y[/latex].
[latex]\scriptsize \begin{align*}3{{x}^{2}}+6x-36 & =-3{{y}^{2}}-12y\\\therefore 3{{x}^{2}}+6x+3{{y}^{2}}+12y & =36\\\therefore {{x}^{2}}+2x+{{y}^{2}}+4y & =12\quad \text{Complete the squares}\\\therefore {{x}^{2}}+2x+1+{{y}^{2}}+4y+4 & =12+1+4\\\therefore {{(x+1)}^{2}}+{{(y+2)}^{2}} & =17\end{align*}[/latex]
Centre [latex]\scriptsize O[/latex] of the circle is [latex]\scriptsize (-1,-2)[/latex].

1. .
   [latex]\scriptsize \displaystyle \begin{align*}{{m}_{{OA}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{-2-2}}{{-1-0}}\\&=\displaystyle \frac{{-4}}{{-1}}\\&=4\end{align*}[/latex]
   [latex]\scriptsize {{m}_{{\text{tangent}}}}=-\displaystyle \frac{1}{4}[/latex]
2. .
   [latex]\scriptsize \displaystyle \begin{align*}{{m}_{{OB}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{-2-(-1)}}{{-1-(-3)}}\\&=-\displaystyle \frac{1}{2}\end{align*}[/latex]
   [latex]\scriptsize {{m}_{{\text{tangent}}}}=2[/latex]
3. .
   [latex]\scriptsize \displaystyle \begin{align*}{{m}_{{OC}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{-2-(-6)}}{{-1-2}}\\&=-\displaystyle \frac{4}{3}\end{align*}[/latex]
   [latex]\scriptsize {{m}_{{\text{tangent}}}}=\displaystyle \frac{3}{4}[/latex]
4. .
   [latex]\scriptsize \displaystyle \begin{align*}{{m}_{{OD}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{-2-(-3)}}{{-1-5}}\\&=-\displaystyle \frac{1}{6}\end{align*}[/latex]
   [latex]\scriptsize {{m}_{{\text{tangent}}}}=6[/latex]

Back to Exercise 2.1

Exercise 2.2

1. .
   [latex]\scriptsize \begin{align*}{{m}_{{CA}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{-1-(-2)}}{{-2-2}}\\&=-\displaystyle \frac{1}{4}\end{align*}[/latex]
   Therefore, [latex]\scriptsize {{m}_{{\text{tangent}}}}=4[/latex].
   [latex]\scriptsize \displaystyle \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-(-1) & =4\left( {x-(-2)} \right)\\\therefore y+1 & =4x+8\\\therefore y & =4x+7\end{align*}[/latex]
2. .
   1. .
      [latex]\scriptsize \begin{align*}r&={{d}_{{CS}}}=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}\\&=\sqrt{{{{{(3-(-2))}}^{2}}+{{{(4-1)}}^{2}}}}\\&=\sqrt{{{{5}^{2}}+{{3}^{2}}}}\\&=\sqrt{{25+9}}\\&=\sqrt{{34}}\end{align*}[/latex]
      The equation of the circle is [latex]\scriptsize {{(x-3)}^{2}}+{{(y-4)}^{2}}=34[/latex].
   2. [latex]\scriptsize T(6,p)[/latex] lies on the circle. Therefore:
      [latex]\scriptsize \begin{align*}{{(6-3)}^{2}}+{{(p-4)}^{2}} & =34\\\therefore {{3}^{2}}+{{p}^{2}}-8p+16 & =34\\\therefore {{p}^{2}}-8p-9 & =0\\\therefore (p-9)(p+1) & =0\\\therefore p=9\text{ } & \text{or }p=-1\end{align*}[/latex]
      Therefore, [latex]\scriptsize p=9[/latex]. We choose this solution because we can see from the sketch that [latex]\scriptsize T(6,p)[/latex] is a point in the first quadrant where [latex]\scriptsize p\ge 0[/latex].
   3. .
      [latex]\scriptsize \begin{align*}{{m}_{{CT}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{9-4}}{{6-3}}\\&=\displaystyle \frac{5}{3}\end{align*}[/latex]
      Therefore, [latex]\scriptsize {{m}_{{\text{tangent}}}}=-\displaystyle \frac{3}{5}[/latex].
      [latex]\scriptsize \displaystyle \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-9 & =-\displaystyle \frac{3}{5}\left( {x-6} \right)\\\therefore y-9 & =-\displaystyle \frac{3}{5}x+\displaystyle \frac{{18}}{5}\\\therefore y & =-\displaystyle \frac{3}{5}x+\displaystyle \frac{{18+45}}{5}\\&=-\displaystyle \frac{3}{5}x+\displaystyle \frac{{63}}{5}\end{align*}[/latex]
      The equation of the tangent is [latex]\scriptsize \displaystyle y=-\displaystyle \frac{3}{5}x+\displaystyle \frac{{63}}{5}[/latex] or [latex]\scriptsize \displaystyle 5y=-3x+63[/latex].
3. Let the points of tangency be [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex]. Both tangents have a gradient of [latex]\scriptsize m=\displaystyle \frac{1}{2}[/latex]. Therefore, the gradients of the radii to [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex] are [latex]\scriptsize m=-2[/latex]. But both these lines pass through the centre. Therefore, [latex]\scriptsize AB[/latex] is a diameter.
   
   Equation of [latex]\scriptsize AB[/latex]:
   [latex]\scriptsize \displaystyle \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-1 & =-2(x-0)\\\therefore y-1 & =-2x\\\therefore y & =-2x+1\end{align*}[/latex]
   To find [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex], solve [latex]\scriptsize y=-2x+1[/latex] and [latex]\scriptsize {{x}^{2}}+{{(y-1)}^{2}}=80[/latex] simultaneously.
   [latex]\scriptsize y=-2x+1\quad \quad (1)[/latex]
   [latex]\scriptsize {{x}^{2}}+{{(y-1)}^{2}}=80\quad \quad (2)[/latex]
   Substitute [latex]\scriptsize (1)[/latex] into [latex]\scriptsize (2)[/latex]:
   [latex]\scriptsize \begin{align*}{{x}^{2}}+{{\left( {(-2x+1)-1} \right)}^{2}} & =80\\\therefore {{x}^{2}}+4{{x}^{2}} & =80\\\therefore 5{{x}^{2}} & =80\\\therefore {{x}^{2}} & =16\\\therefore x & =\pm 4\end{align*}[/latex]
   Substitute [latex]\scriptsize x=-4[/latex] into [latex]\scriptsize (1)[/latex]:
   [latex]\scriptsize \begin{align*}y & =-2(-4)+1\\\therefore y & =9\end{align*}[/latex]
   [latex]\scriptsize A(-4,9)[/latex]
   Substitute [latex]\scriptsize x=4[/latex] into [latex]\scriptsize (1)[/latex]:
   [latex]\scriptsize \begin{align*}y & =-2(4)+1\\\therefore y & =-7\end{align*}[/latex]
   [latex]\scriptsize B(4,-7)[/latex]
   Tangent at [latex]\scriptsize A[/latex]:
   [latex]\scriptsize \displaystyle \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-\left( 9 \right) & =\displaystyle \frac{1}{2}\left( {x-(-4)} \right)\\\therefore y-9 & =\displaystyle \frac{1}{2}x+2\\\therefore y & =\displaystyle \frac{1}{2}x+11\end{align*}[/latex]
   Tangent at [latex]\scriptsize B[/latex]:
   [latex]\scriptsize \displaystyle \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-\left( {-7} \right) & =\displaystyle \frac{1}{2}\left( {x-4} \right)\\\therefore y+7 & =\displaystyle \frac{1}{2}x-2\\\therefore y & =\displaystyle \frac{1}{2}x-9\end{align*}[/latex]

Back to Exercise 2.2

Unit 2: Assessment

1. .
   1. .
      [latex]\scriptsize \begin{align*}{{d}_{{AB}}}&=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}\\&=\sqrt{{{{{\left( {1-(-3)} \right)}}^{2}}+{{{\left( {4-(-2)} \right)}}^{2}}}}\\&=\sqrt{{{{4}^{2}}+{{6}^{2}}}}\\&=\sqrt{{16+36}}\\&=\sqrt{{52}}\\&=2\sqrt{{13}}\end{align*}[/latex]
      Therefore, radius of the circle is [latex]\scriptsize \sqrt{{13}}[/latex].
      The midpoint of [latex]\scriptsize AB[/latex] is the centre of the circle.
      [latex]\scriptsize \begin{align*}\text{midpoin}{{\text{t}}_{{AB}}}&=\left( {\displaystyle \frac{{{{x}_{1}}+{{x}_{2}}}}{2},\displaystyle \frac{{{{y}_{1}}+{{y}_{2}}}}{2}} \right)\\&=\left( {\displaystyle \frac{{1-3}}{2},\displaystyle \frac{{4-2}}{2}} \right)\\&=(-1,1)\end{align*}[/latex]
      The equation of the circle is [latex]\scriptsize {{(x+1)}^{2}}+{{(y-1)}^{2}}=13[/latex].
   2. .
      [latex]\scriptsize \begin{align*}{{m}_{{\text{radius}}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{1-(-2)}}{{-1-(-3)}}\\&=\displaystyle \frac{3}{2}\end{align*}[/latex]
      Therefore, [latex]\scriptsize {{m}_{{\text{tangent}}}}=-\displaystyle \frac{2}{3}[/latex].
      [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-(-2) & =-\displaystyle \frac{2}{3}\left( {x-(-3)} \right)\\\therefore y+2 & =-\displaystyle \frac{2}{3}x-2\\\therefore y & =-\displaystyle \frac{2}{3}x-4\end{align*}[/latex]
      The equation of the tangent at [latex]\scriptsize A[/latex] is [latex]\scriptsize y=-\displaystyle \frac{2}{3}x-4[/latex].
2. .
   1. .
      [latex]\scriptsize \begin{align*}{{m}_{{MB}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{1-(-3)}}{{3-6}}\\&=-\displaystyle \frac{4}{3}\end{align*}[/latex]
      [latex]\scriptsize \displaystyle \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-1 & =-\displaystyle \frac{4}{3}\left( {x-3} \right)\\\therefore y-1 & =-\displaystyle \frac{4}{3}x+4\\\therefore y & =-\displaystyle \frac{4}{3}x+5\end{align*}[/latex]
      The equation of [latex]\scriptsize MB[/latex] is [latex]\scriptsize y=-\displaystyle \frac{4}{3}x+5[/latex]. [latex]\scriptsize A[/latex] is the y-intercept of [latex]\scriptsize MB[/latex]. Therefore, the coordinates of [latex]\scriptsize A[/latex] are [latex]\scriptsize (0,5)[/latex].
   2. [latex]\scriptsize {{m}_{{DC}}}=\displaystyle \frac{3}{4}[/latex] (tangent perpendicular to radius at point of tangency)
      [latex]\scriptsize \displaystyle \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-(-3) & =\displaystyle \frac{3}{4}\left( {x-6} \right)\\\therefore y+3 & =\displaystyle \frac{3}{4}x-\displaystyle \frac{{18}}{4}\\\therefore y & =\displaystyle \frac{3}{4}x-\left( {\displaystyle \frac{{18+12}}{4}} \right)\\&=\displaystyle \frac{3}{4}x-\displaystyle \frac{{30}}{4}\end{align*}[/latex]
      The equation of the tangent at [latex]\scriptsize B[/latex] is [latex]\scriptsize y=\displaystyle \frac{3}{4}x-\displaystyle \frac{{30}}{4}[/latex].
3. .
   1. .
      [latex]\scriptsize \begin{align*} m_{AB}&=\displaystyle \frac{y_2-y_1}{x_2-x_1}\\ &=\displaystyle \frac{-1-(-5)}{1-(-1)}\\&=\displaystyle \frac{4}{2}\\&=2\end{align*}[/latex]
      Therefore, [latex]\scriptsize {{m}_{{FG}}}=-\displaystyle \frac{1}{2}[/latex].
      [latex]\scriptsize \displaystyle \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-(-5) & =-\displaystyle \frac{1}{2}\left( {x-(-1)} \right)\\\therefore y+5 & =-\displaystyle \frac{1}{2}x-\displaystyle \frac{1}{2}\\\therefore y & =-\displaystyle \frac{1}{2}x-\displaystyle \frac{{11}}{2}\end{align*}[/latex]
      The equation of tangent [latex]\scriptsize FG[/latex] is [latex]\scriptsize \displaystyle y =-\displaystyle \frac{1}{2}x-\displaystyle \frac{{11}}{2}[/latex].
   2. Circle is of the form [latex]\scriptsize {{(x-1)}^{2}}+{{(y+1)}^{2}}={{r}^{2}}[/latex].
      [latex]\scriptsize \begin{align*}r={{d}_{{AB}}}&=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}\\&=\sqrt{{{{{\left( {1-(-1)} \right)}}^{2}}+{{{\left( {-1-(-5)} \right)}}^{2}}}}\\&=\sqrt{{{{2}^{2}}+{{{(4)}}^{2}}}}\\&=\sqrt{{4+16}}\\&=\sqrt{{20}}\\&=2\sqrt{5}\end{align*}[/latex]
      Therefore, the equation of the circle is [latex]\scriptsize {{(x-1)}^{2}}+{{(y+1)}^{2}}=20[/latex].
   3. [latex]\scriptsize BA\bot FA[/latex]. Therefore [latex]\scriptsize \Delta FAB[/latex] is a right-angled triangle. Therefore:
      [latex]\scriptsize \begin{align*}F{{B}^{2}} & =F{{A}^{2}}+A{{B}^{2}}\\\therefore F{{A}^{2}} & =F{{B}^{2}}-A{{B}^{2}}\\\therefore F{{A}^{2}} & =69-20=49\\\therefore FA & =7\end{align*}[/latex]
      Note: Because [latex]\scriptsize FA[/latex] is a length, we can ignore the negative root.
4. .
   1. Equation is of the form [latex]\scriptsize {{(x+4)}^{2}}+{{(y-2)}^{2}}={{r}^{2}}[/latex].
      [latex]\scriptsize \begin{align*}r=d_{MO}&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\&=\sqrt{(-4-0)^2+(2-0)^2}\\&=\sqrt{16+4}\\&=\sqrt{20}\\&=2\sqrt{5}\end{align*}[/latex]
      Therefore, the equation of the circle is [latex]\scriptsize (x+4)^2+(y-2)^2=20[/latex].
   2. [latex]\scriptsize N(-2,y)[/latex] lies on the circle.
      [latex]\scriptsize \begin{align*}{{((-2)+4)}^{2}}+{{(y-2)}^{2}} & =20\\\therefore 4+{{y}^{2}}-4y+4 & =20\\\therefore {{y}^{2}}-4y-12 & =0\\\therefore (y-6)(y+2) & =0\\\therefore y=6\text{ } & \text{or }y=-2\end{align*}[/latex]
      Therefore, at N [latex]\scriptsize y=6[/latex].
   3. .
      [latex]\scriptsize \begin{align*}{{m}_{{MO}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{2-0}}{{-4-0}}\\&=-\displaystyle \frac{1}{2}\end{align*}[/latex]
      Therefore, [latex]\scriptsize {{m}_{{OP}}}=2[/latex] (tangent perpendicular to radius as point of tangency).
5. .
   1. .
      [latex]\scriptsize \begin{align*}{{r}^{2}} & =36\\\therefore r & =6\end{align*}[/latex]
   2. [latex]\scriptsize (2,a)[/latex] lies on the circle. Therefore:
      [latex]\scriptsize \begin{align*}{{(2)}^{2}}+{{a}^{2}} & =36\\\therefore {{a}^{2}} & =32\\\therefore a & =\pm \sqrt{{32}}\\ & =\pm 4\sqrt{2}\end{align*}[/latex]
      Therefore, [latex]\scriptsize a=4\sqrt{2}[/latex].
   3. [latex]\scriptsize QR\parallel OS[/latex] ([latex]\scriptsize OQRS[/latex] is a parallelogram, given)
      But [latex]\scriptsize OS[/latex] is on the x-axis. Therefore, y-coordinate of [latex]\scriptsize Q[/latex] is equal to y-coordinate of [latex]\scriptsize R[/latex]. Therefore, [latex]\scriptsize n=2[/latex].
      [latex]\scriptsize QR=OS[/latex] ([latex]\scriptsize OQRS[/latex] is a parallelogram, given)
      But [latex]\scriptsize OS=r=6=QR[/latex]. Therefore, [latex]\scriptsize m=2+6=8[/latex].

Back to Unit 2: Assessment